CAT DILR Questions | CAT Logical Reasoning questions
This section contains CAT Past year Questions based on LOGICAL REASONING — Questions based on Fact, Judgement and Inference; Syllogism; Sentence and Conclusion; Arguments. CAT Logical Reasoning | CAT Past Year DILR QuestionsComprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
The game of QUIET is played between two teams. Six teams, numbered 1, 2, 3, 4, 5, and 6, play in a QUIET tournament. These teams are divided equally into two groups. In the tournament, each team plays every other team in the same group only once, and each team in the other group exactly twice. The tournament has several rounds, each of which consists of a few games. Every team plays exactly one game in each round.
The following additional facts are known about the schedule of games in the tournament.
1. Each team played against a team from the other group in Round 8.
2. In Round 4 and Round 7, the match-ups, that is the pair of teams playing against each other, were identical. In Round 5 and Round 8, the match-ups were identical.
3. Team 4 played Team 6 in both Round 1 and Round 2.
4. Team 1 played Team 5 ONLY once and that was in Round 2.
5. Team 3 played Team 4 in Round 3. Team 1 played Team 6 in Round 6.
6. In Round 8, Team 3 played Team 6, while Team 2 played Team 5.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
The game of QUIET is played between two teams. Six teams, numbered 1, 2, 3, 4, 5, and 6, play in a QUIET tournament. These teams are divided equally into two groups. In the tournament, each team plays every other team in the same group only once, and each team in the other group exactly twice. The tournament has several rounds, each of which consists of a few games. Every team plays exactly one game in each round.
The following additional facts are known about the schedule of games in the tournament.
1. Each team played against a team from the other group in Round 8.
2. In Round 4 and Round 7, the match-ups, that is the pair of teams playing against each other, were identical. In Round 5 and Round 8, the match-ups were identical.
3. Team 4 played Team 6 in both Round 1 and Round 2.
4. Team 1 played Team 5 ONLY once and that was in Round 2.
5. Team 3 played Team 4 in Round 3. Team 1 played Team 6 in Round 6.
6. In Round 8, Team 3 played Team 6, while Team 2 played Team 5.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
The game of QUIET is played between two teams. Six teams, numbered 1, 2, 3, 4, 5, and 6, play in a QUIET tournament. These teams are divided equally into two groups. In the tournament, each team plays every other team in the same group only once, and each team in the other group exactly twice. The tournament has several rounds, each of which consists of a few games. Every team plays exactly one game in each round.
The following additional facts are known about the schedule of games in the tournament.
1. Each team played against a team from the other group in Round 8.
2. In Round 4 and Round 7, the match-ups, that is the pair of teams playing against each other, were identical. In Round 5 and Round 8, the match-ups were identical.
3. Team 4 played Team 6 in both Round 1 and Round 2.
4. Team 1 played Team 5 ONLY once and that was in Round 2.
5. Team 3 played Team 4 in Round 3. Team 1 played Team 6 in Round 6.
6. In Round 8, Team 3 played Team 6, while Team 2 played Team 5.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
The game of QUIET is played between two teams. Six teams, numbered 1, 2, 3, 4, 5, and 6, play in a QUIET tournament. These teams are divided equally into two groups. In the tournament, each team plays every other team in the same group only once, and each team in the other group exactly twice. The tournament has several rounds, each of which consists of a few games. Every team plays exactly one game in each round.
The following additional facts are known about the schedule of games in the tournament.
1. Each team played against a team from the other group in Round 8.
2. In Round 4 and Round 7, the match-ups, that is the pair of teams playing against each other, were identical. In Round 5 and Round 8, the match-ups were identical.
3. Team 4 played Team 6 in both Round 1 and Round 2.
4. Team 1 played Team 5 ONLY once and that was in Round 2.
5. Team 3 played Team 4 in Round 3. Team 1 played Team 6 in Round 6.
6. In Round 8, Team 3 played Team 6, while Team 2 played Team 5.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
The game of QUIET is played between two teams. Six teams, numbered 1, 2, 3, 4, 5, and 6, play in a QUIET tournament. These teams are divided equally into two groups. In the tournament, each team plays every other team in the same group only once, and each team in the other group exactly twice. The tournament has several rounds, each of which consists of a few games. Every team plays exactly one game in each round.
The following additional facts are known about the schedule of games in the tournament.
1. Each team played against a team from the other group in Round 8.
2. In Round 4 and Round 7, the match-ups, that is the pair of teams playing against each other, were identical. In Round 5 and Round 8, the match-ups were identical.
3. Team 4 played Team 6 in both Round 1 and Round 2.
4. Team 1 played Team 5 ONLY once and that was in Round 2.
5. Team 3 played Team 4 in Round 3. Team 1 played Team 6 in Round 6.
6. In Round 8, Team 3 played Team 6, while Team 2 played Team 5.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly
There are nine boxes arranged in a 3×3 array as shown in Tables 1 and 2. Each box contains three sacks. Each sack has a certain number of coins, between 1 and 9, both inclusive.
The average number of coins per sack in the boxes are all distinct integers. The total number of coins in each row is the same. The total number of coins in each column is also the same.
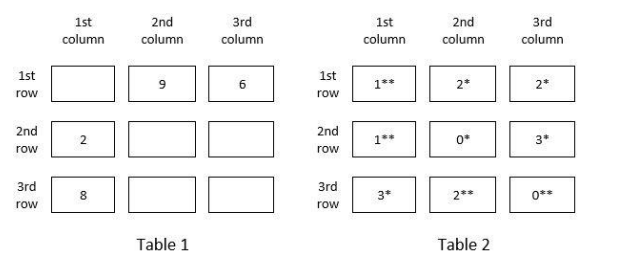
Table 1 gives information regarding the median of the numbers of coins in the three sacks in a box for some of the boxes. In Table 2 each box has a number which represents the number of sacks in that box having more than 5 coins. That number is followed by a * if the sacks in that box satisfy exactly one among the following three conditions, and it is followed by ** if two or more of these conditions are satisfied.
i) The minimum among the numbers of coins in the three sacks in the box is 1.
ii) The median of the numbers of coins in the three sacks is 1.
iii) The maximum among the numbers of coins in the three sacks in the box is 9.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly
There are nine boxes arranged in a 3×3 array as shown in Tables 1 and 2. Each box contains three sacks. Each sack has a certain number of coins, between 1 and 9, both inclusive.
The average number of coins per sack in the boxes are all distinct integers. The total number of coins in each row is the same. The total number of coins in each column is also the same.

Table 1 gives information regarding the median of the numbers of coins in the three sacks in a box for some of the boxes. In Table 2 each box has a number which represents the number of sacks in that box having more than 5 coins. That number is followed by a * if the sacks in that box satisfy exactly one among the following three conditions, and it is followed by ** if two or more of these conditions are satisfied.
i) The minimum among the numbers of coins in the three sacks in the box is 1.
ii) The median of the numbers of coins in the three sacks is 1.
iii) The maximum among the numbers of coins in the three sacks in the box is 9.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly
There are nine boxes arranged in a 3×3 array as shown in Tables 1 and 2. Each box contains three sacks. Each sack has a certain number of coins, between 1 and 9, both inclusive.
The average number of coins per sack in the boxes are all distinct integers. The total number of coins in each row is the same. The total number of coins in each column is also the same.

Table 1 gives information regarding the median of the numbers of coins in the three sacks in a box for some of the boxes. In Table 2 each box has a number which represents the number of sacks in that box having more than 5 coins. That number is followed by a * if the sacks in that box satisfy exactly one among the following three conditions, and it is followed by ** if two or more of these conditions are satisfied.
i) The minimum among the numbers of coins in the three sacks in the box is 1.
ii) The median of the numbers of coins in the three sacks is 1.
iii) The maximum among the numbers of coins in the three sacks in the box is 9.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly
There are nine boxes arranged in a 3×3 array as shown in Tables 1 and 2. Each box contains three sacks. Each sack has a certain number of coins, between 1 and 9, both inclusive.
The average number of coins per sack in the boxes are all distinct integers. The total number of coins in each row is the same. The total number of coins in each column is also the same.

Table 1 gives information regarding the median of the numbers of coins in the three sacks in a box for some of the boxes. In Table 2 each box has a number which represents the number of sacks in that box having more than 5 coins. That number is followed by a * if the sacks in that box satisfy exactly one among the following three conditions, and it is followed by ** if two or more of these conditions are satisfied.
i) The minimum among the numbers of coins in the three sacks in the box is 1.
ii) The median of the numbers of coins in the three sacks is 1.
iii) The maximum among the numbers of coins in the three sacks in the box is 9.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly
There are nine boxes arranged in a 3×3 array as shown in Tables 1 and 2. Each box contains three sacks. Each sack has a certain number of coins, between 1 and 9, both inclusive.
The average number of coins per sack in the boxes are all distinct integers. The total number of coins in each row is the same. The total number of coins in each column is also the same.

Table 1 gives information regarding the median of the numbers of coins in the three sacks in a box for some of the boxes. In Table 2 each box has a number which represents the number of sacks in that box having more than 5 coins. That number is followed by a * if the sacks in that box satisfy exactly one among the following three conditions, and it is followed by ** if two or more of these conditions are satisfied.
i) The minimum among the numbers of coins in the three sacks in the box is 1.
ii) The median of the numbers of coins in the three sacks is 1.
iii) The maximum among the numbers of coins in the three sacks in the box is 9.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly
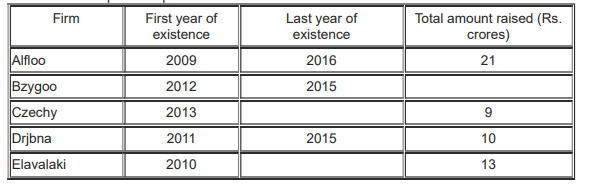
Odsville has five firms – Alfloo, Bzygoo, Czechy, Drjbna and Elavalaki. Each of these firms was founded in some year and also closed down a few years later.
Each firm raised Rs. 1 crore in its first and last year of existence. The amount each firm raised every year increased until it reached a maximum, and then decreased until the firm closed down. No firm raised the same amount of money in two consecutive years. Each annual increase and decrease was either by Rs. 1 crore or by Rs. 2 crores.
The table below provides partial information about the five firms:
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly
Odsville has five firms – Alfloo, Bzygoo, Czechy, Drjbna and Elavalaki. Each of these firms was founded in some year and also closed down a few years later.
Each firm raised Rs. 1 crore in its first and last year of existence. The amount each firm raised every year increased until it reached a maximum, and then decreased until the firm closed down. No firm raised the same amount of money in two consecutive years. Each annual increase and decrease was either by Rs. 1 crore or by Rs. 2 crores.
The table below provides partial information about the five firms:

Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly
Odsville has five firms – Alfloo, Bzygoo, Czechy, Drjbna and Elavalaki. Each of these firms was founded in some year and also closed down a few years later.
Each firm raised Rs. 1 crore in its first and last year of existence. The amount each firm raised every year increased until it reached a maximum, and then decreased until the firm closed down. No firm raised the same amount of money in two consecutive years. Each annual increase and decrease was either by Rs. 1 crore or by Rs. 2 crores.
The table below provides partial information about the five firms:

CAT/2023.2(DILR)
Question. 13
What is the largest possible total amount of money (in Rs. crores) that could have been raised in 2013?
17
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly
Odsville has five firms – Alfloo, Bzygoo, Czechy, Drjbna and Elavalaki. Each of these firms was founded in some year and also closed down a few years later.
Each firm raised Rs. 1 crore in its first and last year of existence. The amount each firm raised every year increased until it reached a maximum, and then decreased until the firm closed down. No firm raised the same amount of money in two consecutive years. Each annual increase and decrease was either by Rs. 1 crore or by Rs. 2 crores.
The table below provides partial information about the five firms:

Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly
Odsville has five firms – Alfloo, Bzygoo, Czechy, Drjbna and Elavalaki. Each of these firms was founded in some year and also closed down a few years later.
Each firm raised Rs. 1 crore in its first and last year of existence. The amount each firm raised every year increased until it reached a maximum, and then decreased until the firm closed down. No firm raised the same amount of money in two consecutive years. Each annual increase and decrease was either by Rs. 1 crore or by Rs. 2 crores.
The table below provides partial information about the five firms:

Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
Faculty members in a management school can belong to one of four departments – Finance and Accounting (F&A), Marketing and Strategy (M&S), Operations and Quants (O&Q) and Behaviour and Human Resources (B&H). The numbers of faculty members in F&A, M&S, O&Q and B&H departments are 9, 7, 5 and 3 respectively.
Prof. Pakrasi, Prof. Qureshi, Prof. Ramaswamy and Prof. Samuel are four members of the school's faculty who were candidates for the post of the Dean of the school. Only one of the candidates was from O&Q.
Every faculty member, including the four candidates, voted for the post. In each department, all the faculty members who were not candidates voted for the same candidate. The rules for the election are listed below.
1. There cannot be more than two candidates from a single department.
2. A candidate cannot vote for himself/herself.
3. Faculty members cannot vote for a candidate from their own department.
After the election, it was observed that Prof. Pakrasi received 3 votes, Prof. Qureshi received 14 votes, Prof. Ramaswamy received 6 votes and Prof. Samuel received 1 vote. Prof. Pakrasi voted for Prof. Ramaswamy, Prof. Qureshi for Prof. Samuel, Prof. Ramaswamy for Prof. Qureshi and Prof. Samuel for Prof. Pakras.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
Faculty members in a management school can belong to one of four departments – Finance and Accounting (F&A), Marketing and Strategy (M&S), Operations and Quants (O&Q) and Behaviour and Human Resources (B&H). The numbers of faculty members in F&A, M&S, O&Q and B&H departments are 9, 7, 5 and 3 respectively.
Prof. Pakrasi, Prof. Qureshi, Prof. Ramaswamy and Prof. Samuel are four members of the school's faculty who were candidates for the post of the Dean of the school. Only one of the candidates was from O&Q.
Every faculty member, including the four candidates, voted for the post. In each department, all the faculty members who were not candidates voted for the same candidate. The rules for the election are listed below.
1. There cannot be more than two candidates from a single department.
2. A candidate cannot vote for himself/herself.
3. Faculty members cannot vote for a candidate from their own department.
After the election, it was observed that Prof. Pakrasi received 3 votes, Prof. Qureshi received 14 votes, Prof. Ramaswamy received 6 votes and Prof. Samuel received 1 vote. Prof. Pakrasi voted for Prof. Ramaswamy, Prof. Qureshi for Prof. Samuel, Prof. Ramaswamy for Prof. Qureshi and Prof. Samuel for Prof. Pakras.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
Faculty members in a management school can belong to one of four departments – Finance and Accounting (F&A), Marketing and Strategy (M&S), Operations and Quants (O&Q) and Behaviour and Human Resources (B&H). The numbers of faculty members in F&A, M&S, O&Q and B&H departments are 9, 7, 5 and 3 respectively.
Prof. Pakrasi, Prof. Qureshi, Prof. Ramaswamy and Prof. Samuel are four members of the school's faculty who were candidates for the post of the Dean of the school. Only one of the candidates was from O&Q.
Every faculty member, including the four candidates, voted for the post. In each department, all the faculty members who were not candidates voted for the same candidate. The rules for the election are listed below.
1. There cannot be more than two candidates from a single department.
2. A candidate cannot vote for himself/herself.
3. Faculty members cannot vote for a candidate from their own department.
After the election, it was observed that Prof. Pakrasi received 3 votes, Prof. Qureshi received 14 votes, Prof. Ramaswamy received 6 votes and Prof. Samuel received 1 vote. Prof. Pakrasi voted for Prof. Ramaswamy, Prof. Qureshi for Prof. Samuel, Prof. Ramaswamy for Prof. Qureshi and Prof. Samuel for Prof. Pakras.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
Faculty members in a management school can belong to one of four departments – Finance and Accounting (F&A), Marketing and Strategy (M&S), Operations and Quants (O&Q) and Behaviour and Human Resources (B&H). The numbers of faculty members in F&A, M&S, O&Q and B&H departments are 9, 7, 5 and 3 respectively.
Prof. Pakrasi, Prof. Qureshi, Prof. Ramaswamy and Prof. Samuel are four members of the school's faculty who were candidates for the post of the Dean of the school. Only one of the candidates was from O&Q.
Every faculty member, including the four candidates, voted for the post. In each department, all the faculty members who were not candidates voted for the same candidate. The rules for the election are listed below.
1. There cannot be more than two candidates from a single department.
2. A candidate cannot vote for himself/herself.
3. Faculty members cannot vote for a candidate from their own department.
After the election, it was observed that Prof. Pakrasi received 3 votes, Prof. Qureshi received 14 votes, Prof. Ramaswamy received 6 votes and Prof. Samuel received 1 vote. Prof. Pakrasi voted for Prof. Ramaswamy, Prof. Qureshi for Prof. Samuel, Prof. Ramaswamy for Prof. Qureshi and Prof. Samuel for Prof. Pakras.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
Faculty members in a management school can belong to one of four departments – Finance and Accounting (F&A), Marketing and Strategy (M&S), Operations and Quants (O&Q) and Behaviour and Human Resources (B&H). The numbers of faculty members in F&A, M&S, O&Q and B&H departments are 9, 7, 5 and 3 respectively.
Prof. Pakrasi, Prof. Qureshi, Prof. Ramaswamy and Prof. Samuel are four members of the school's faculty who were candidates for the post of the Dean of the school. Only one of the candidates was from O&Q.
Every faculty member, including the four candidates, voted for the post. In each department, all the faculty members who were not candidates voted for the same candidate. The rules for the election are listed below.
1. There cannot be more than two candidates from a single department.
2. A candidate cannot vote for himself/herself.
3. Faculty members cannot vote for a candidate from their own department.
After the election, it was observed that Prof. Pakrasi received 3 votes, Prof. Qureshi received 14 votes, Prof. Ramaswamy received 6 votes and Prof. Samuel received 1 vote. Prof. Pakrasi voted for Prof. Ramaswamy, Prof. Qureshi for Prof. Samuel, Prof. Ramaswamy for Prof. Qureshi and Prof. Samuel for Prof. Pakras.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
The schematic diagram below shows 12 rectangular houses in a housing complex. House numbers are mentioned in the rectangles representing the houses. The houses are located in six columns – Column-A through Column-F, and two rows – Row-1 and Row-2. The houses are divided into two blocks - Block XX and Block YY. The diagram also shows two roads, one passing in front of the houses in Row-2 and another between the two blocks.

Some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The road adjacency value of a house is the number of its sides adjacent to a road. For example, the road adjacency values of C2, F2, and B1 are 2, 1, and 0, respectively. The neighbour count of a house is the number of sides of that house adjacent to occupied houses in the same block. For example, E1 and C1 can have the maximum possible neighbour counts of 3 and 2, respectively.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbour count).
The following information is also known.
1. The maximum quoted price of a house in Block XX is Rs. 24 lakhs. The minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column-E.
2. Row-1 has two occupied houses, one in each block.
3. Both houses in Column-E are vacant. Each of Column-D and Column-F has at least one occupied house.
4. There is only one house with parking space in Block YY.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
The schematic diagram below shows 12 rectangular houses in a housing complex. House numbers are mentioned in the rectangles representing the houses. The houses are located in six columns – Column-A through Column-F, and two rows – Row-1 and Row-2. The houses are divided into two blocks - Block XX and Block YY. The diagram also shows two roads, one passing in front of the houses in Row-2 and another between the two blocks.

Some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The road adjacency value of a house is the number of its sides adjacent to a road. For example, the road adjacency values of C2, F2, and B1 are 2, 1, and 0, respectively. The neighbour count of a house is the number of sides of that house adjacent to occupied houses in the same block. For example, E1 and C1 can have the maximum possible neighbour counts of 3 and 2, respectively.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbour count).
The following information is also known.
1. The maximum quoted price of a house in Block XX is Rs. 24 lakhs. The minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column-E.
2. Row-1 has two occupied houses, one in each block.
3. Both houses in Column-E are vacant. Each of Column-D and Column-F has at least one occupied house.
4. There is only one house with parking space in Block YY.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
The schematic diagram below shows 12 rectangular houses in a housing complex. House numbers are mentioned in the rectangles representing the houses. The houses are located in six columns – Column-A through Column-F, and two rows – Row-1 and Row-2. The houses are divided into two blocks - Block XX and Block YY. The diagram also shows two roads, one passing in front of the houses in Row-2 and another between the two blocks.

Some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The road adjacency value of a house is the number of its sides adjacent to a road. For example, the road adjacency values of C2, F2, and B1 are 2, 1, and 0, respectively. The neighbour count of a house is the number of sides of that house adjacent to occupied houses in the same block. For example, E1 and C1 can have the maximum possible neighbour counts of 3 and 2, respectively.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbour count).
The following information is also known.
1. The maximum quoted price of a house in Block XX is Rs. 24 lakhs. The minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column-E.
2. Row-1 has two occupied houses, one in each block.
3. Both houses in Column-E are vacant. Each of Column-D and Column-F has at least one occupied house.
4. There is only one house with parking space in Block YY.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
The schematic diagram below shows 12 rectangular houses in a housing complex. House numbers are mentioned in the rectangles representing the houses. The houses are located in six columns – Column-A through Column-F, and two rows – Row-1 and Row-2. The houses are divided into two blocks - Block XX and Block YY. The diagram also shows two roads, one passing in front of the houses in Row-2 and another between the two blocks.

Some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The road adjacency value of a house is the number of its sides adjacent to a road. For example, the road adjacency values of C2, F2, and B1 are 2, 1, and 0, respectively. The neighbour count of a house is the number of sides of that house adjacent to occupied houses in the same block. For example, E1 and C1 can have the maximum possible neighbour counts of 3 and 2, respectively.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbour count).
The following information is also known.
1. The maximum quoted price of a house in Block XX is Rs. 24 lakhs. The minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column-E.
2. Row-1 has two occupied houses, one in each block.
3. Both houses in Column-E are vacant. Each of Column-D and Column-F has at least one occupied house.
4. There is only one house with parking space in Block YY.
CAT/2023.1(DILR)
Question. 24
What is the maximum possible quoted price (in lakhs of Rs.) for a vacant house in Column-E?
21
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
The schematic diagram below shows 12 rectangular houses in a housing complex. House numbers are mentioned in the rectangles representing the houses. The houses are located in six columns – Column-A through Column-F, and two rows – Row-1 and Row-2. The houses are divided into two blocks - Block XX and Block YY. The diagram also shows two roads, one passing in front of the houses in Row-2 and another between the two blocks.

Some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The road adjacency value of a house is the number of its sides adjacent to a road. For example, the road adjacency values of C2, F2, and B1 are 2, 1, and 0, respectively. The neighbour count of a house is the number of sides of that house adjacent to occupied houses in the same block. For example, E1 and C1 can have the maximum possible neighbour counts of 3 and 2, respectively.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbour count).
The following information is also known.
1. The maximum quoted price of a house in Block XX is Rs. 24 lakhs. The minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column-E.
2. Row-1 has two occupied houses, one in each block.
3. Both houses in Column-E are vacant. Each of Column-D and Column-F has at least one occupied house.
4. There is only one house with parking space in Block YY.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
All the first-year students in the computer science (CS) department in a university take both the courses (i) AI and (ii) ML. Students from other departments (non-CS students) can also take one of these two courses, but not both. Students who fail in a course get an F grade; others pass and are awarded A or B or C grades depending on their performance. The following are some additional facts about the number of students who took these two courses this year and the grades they obtained.
1. The numbers of non-CS students who took AI and ML were in the ratio 2 : 5.
2. The number of non-CS students who took either AI or ML was equal to the number of CS students.
3. The numbers of non-CS students who failed in the two courses were the same and their total is equal to the number of CS students who got a C grade in ML.
4. In both the courses, 50% of the students who passed got a B grade. But, while the numbers of students who got A and C grades were the same for AI, they were in the ratio 3 : 2 for ML.
5. No CS student failed in AI, while no non-CS student got an A grade in AI.
6. The numbers of CS students who got A, B and C grades respectively in AI were in the ratio 3 : 5 : 2, while in ML the ratio was 4 : 5 : 2.
7. The ratio of the total number of non-CS students failing in one of the two courses to the number of CS students failing in one of the two courses was 3 : 1.
8. 30 students failed in ML.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
All the first-year students in the computer science (CS) department in a university take both the courses (i) AI and (ii) ML. Students from other departments (non-CS students) can also take one of these two courses, but not both. Students who fail in a course get an F grade; others pass and are awarded A or B or C grades depending on their performance. The following are some additional facts about the number of students who took these two courses this year and the grades they obtained.
1. The numbers of non-CS students who took AI and ML were in the ratio 2 : 5.
2. The number of non-CS students who took either AI or ML was equal to the number of CS students.
3. The numbers of non-CS students who failed in the two courses were the same and their total is equal to the number of CS students who got a C grade in ML.
4. In both the courses, 50% of the students who passed got a B grade. But, while the numbers of students who got A and C grades were the same for AI, they were in the ratio 3 : 2 for ML.
5. No CS student failed in AI, while no non-CS student got an A grade in AI.
6. The numbers of CS students who got A, B and C grades respectively in AI were in the ratio 3 : 5 : 2, while in ML the ratio was 4 : 5 : 2.
7. The ratio of the total number of non-CS students failing in one of the two courses to the number of CS students failing in one of the two courses was 3 : 1.
8. 30 students failed in ML.
12
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
All the first-year students in the computer science (CS) department in a university take both the courses (i) AI and (ii) ML. Students from other departments (non-CS students) can also take one of these two courses, but not both. Students who fail in a course get an F grade; others pass and are awarded A or B or C grades depending on their performance. The following are some additional facts about the number of students who took these two courses this year and the grades they obtained.
1. The numbers of non-CS students who took AI and ML were in the ratio 2 : 5.
2. The number of non-CS students who took either AI or ML was equal to the number of CS students.
3. The numbers of non-CS students who failed in the two courses were the same and their total is equal to the number of CS students who got a C grade in ML.
4. In both the courses, 50% of the students who passed got a B grade. But, while the numbers of students who got A and C grades were the same for AI, they were in the ratio 3 : 2 for ML.
5. No CS student failed in AI, while no non-CS student got an A grade in AI.
6. The numbers of CS students who got A, B and C grades respectively in AI were in the ratio 3 : 5 : 2, while in ML the ratio was 4 : 5 : 2.
7. The ratio of the total number of non-CS students failing in one of the two courses to the number of CS students failing in one of the two courses was 3 : 1.
8. 30 students failed in ML.
27
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
All the first-year students in the computer science (CS) department in a university take both the courses (i) AI and (ii) ML. Students from other departments (non-CS students) can also take one of these two courses, but not both. Students who fail in a course get an F grade; others pass and are awarded A or B or C grades depending on their performance. The following are some additional facts about the number of students who took these two courses this year and the grades they obtained.
1. The numbers of non-CS students who took AI and ML were in the ratio 2 : 5.
2. The number of non-CS students who took either AI or ML was equal to the number of CS students.
3. The numbers of non-CS students who failed in the two courses were the same and their total is equal to the number of CS students who got a C grade in ML.
4. In both the courses, 50% of the students who passed got a B grade. But, while the numbers of students who got A and C grades were the same for AI, they were in the ratio 3 : 2 for ML.
5. No CS student failed in AI, while no non-CS student got an A grade in AI.
6. The numbers of CS students who got A, B and C grades respectively in AI were in the ratio 3 : 5 : 2, while in ML the ratio was 4 : 5 : 2.
7. The ratio of the total number of non-CS students failing in one of the two courses to the number of CS students failing in one of the two courses was 3 : 1.
8. 30 students failed in ML.
27
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
All the first-year students in the computer science (CS) department in a university take both the courses (i) AI and (ii) ML. Students from other departments (non-CS students) can also take one of these two courses, but not both. Students who fail in a course get an F grade; others pass and are awarded A or B or C grades depending on their performance. The following are some additional facts about the number of students who took these two courses this year and the grades they obtained.
1. The numbers of non-CS students who took AI and ML were in the ratio 2 : 5.
2. The number of non-CS students who took either AI or ML was equal to the number of CS students.
3. The numbers of non-CS students who failed in the two courses were the same and their total is equal to the number of CS students who got a C grade in ML.
4. In both the courses, 50% of the students who passed got a B grade. But, while the numbers of students who got A and C grades were the same for AI, they were in the ratio 3 : 2 for ML.
5. No CS student failed in AI, while no non-CS student got an A grade in AI.
6. The numbers of CS students who got A, B and C grades respectively in AI were in the ratio 3 : 5 : 2, while in ML the ratio was 4 : 5 : 2.
7. The ratio of the total number of non-CS students failing in one of the two courses to the number of CS students failing in one of the two courses was 3 : 1.
8. 30 students failed in ML.
27
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
Pulak, Qasim, Ritesh, and Suresh participated in a tournament comprising of eight rounds. In each round, they formed two pairs, with each of them being in exactly one pair. The only restriction in the pairing was that the pairs would change in successive rounds. For example, if Pulak formed a pair with Qasim in the first round, then he would have to form a pair with Ritesh or Suresh in the second round. He would be free to pair with Qasim again in the third round. In each round, each pair decided whether to play the game in that round or not. If they decided not to play, then no money was exchanged between them. If they decided to play, they had to bet either ₹1 or ₹2 in that round. For example, if they chose to bet ₹2, then the player winning the game got ₹2 from the one losing the game. At the beginning of the tournament, the players had ₹10 each. The following table shows partial information about the amounts that the players had at the end of each of the eight rounds. It shows every time a player had ₹10 at the end of a round, as well as every time, at the end of a round, a player had either the minimum or the maximum amount that he would have had across the eight rounds. For example, Suresh had ₹10 at the end of Rounds 1, 3, and 8 and not after any of the other rounds. The maximum amount that he had at the end of any round was ₹13 (at the end of Round 5), and the minimum amount he had at the end of any round was ₹8 (at the end of Round 2). At the end of all other rounds, he must have had either ₹9, ₹11, or ₹12.
It was also known that Pulak and Qasim had the same amount of money with them at the end of Round 4.

Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
Pulak, Qasim, Ritesh, and Suresh participated in a tournament comprising of eight rounds. In each round, they formed two pairs, with each of them being in exactly one pair. The only restriction in the pairing was that the pairs would change in successive rounds. For example, if Pulak formed a pair with Qasim in the first round, then he would have to form a pair with Ritesh or Suresh in the second round. He would be free to pair with Qasim again in the third round. In each round, each pair decided whether to play the game in that round or not. If they decided not to play, then no money was exchanged between them. If they decided to play, they had to bet either ₹1 or ₹2 in that round. For example, if they chose to bet ₹2, then the player winning the game got ₹2 from the one losing the game. At the beginning of the tournament, the players had ₹10 each. The following table shows partial information about the amounts that the players had at the end of each of the eight rounds. It shows every time a player had ₹10 at the end of a round, as well as every time, at the end of a round, a player had either the minimum or the maximum amount that he would have had across the eight rounds. For example, Suresh had ₹10 at the end of Rounds 1, 3, and 8 and not after any of the other rounds. The maximum amount that he had at the end of any round was ₹13 (at the end of Round 5), and the minimum amount he had at the end of any round was ₹8 (at the end of Round 2). At the end of all other rounds, he must have had either ₹9, ₹11, or ₹12.
It was also known that Pulak and Qasim had the same amount of money with them at the end of Round 4.

Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
Pulak, Qasim, Ritesh, and Suresh participated in a tournament comprising of eight rounds. In each round, they formed two pairs, with each of them being in exactly one pair. The only restriction in the pairing was that the pairs would change in successive rounds. For example, if Pulak formed a pair with Qasim in the first round, then he would have to form a pair with Ritesh or Suresh in the second round. He would be free to pair with Qasim again in the third round. In each round, each pair decided whether to play the game in that round or not. If they decided not to play, then no money was exchanged between them. If they decided to play, they had to bet either ₹1 or ₹2 in that round. For example, if they chose to bet ₹2, then the player winning the game got ₹2 from the one losing the game. At the beginning of the tournament, the players had ₹10 each. The following table shows partial information about the amounts that the players had at the end of each of the eight rounds. It shows every time a player had ₹10 at the end of a round, as well as every time, at the end of a round, a player had either the minimum or the maximum amount that he would have had across the eight rounds. For example, Suresh had ₹10 at the end of Rounds 1, 3, and 8 and not after any of the other rounds. The maximum amount that he had at the end of any round was ₹13 (at the end of Round 5), and the minimum amount he had at the end of any round was ₹8 (at the end of Round 2). At the end of all other rounds, he must have had either ₹9, ₹11, or ₹12.
It was also known that Pulak and Qasim had the same amount of money with them at the end of Round 4.

Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
Pulak, Qasim, Ritesh, and Suresh participated in a tournament comprising of eight rounds. In each round, they formed two pairs, with each of them being in exactly one pair. The only restriction in the pairing was that the pairs would change in successive rounds. For example, if Pulak formed a pair with Qasim in the first round, then he would have to form a pair with Ritesh or Suresh in the second round. He would be free to pair with Qasim again in the third round. In each round, each pair decided whether to play the game in that round or not. If they decided not to play, then no money was exchanged between them. If they decided to play, they had to bet either ₹1 or ₹2 in that round. For example, if they chose to bet ₹2, then the player winning the game got ₹2 from the one losing the game. At the beginning of the tournament, the players had ₹10 each. The following table shows partial information about the amounts that the players had at the end of each of the eight rounds. It shows every time a player had ₹10 at the end of a round, as well as every time, at the end of a round, a player had either the minimum or the maximum amount that he would have had across the eight rounds. For example, Suresh had ₹10 at the end of Rounds 1, 3, and 8 and not after any of the other rounds. The maximum amount that he had at the end of any round was ₹13 (at the end of Round 5), and the minimum amount he had at the end of any round was ₹8 (at the end of Round 2). At the end of all other rounds, he must have had either ₹9, ₹11, or ₹12.
It was also known that Pulak and Qasim had the same amount of money with them at the end of Round 4.

Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
Pulak, Qasim, Ritesh, and Suresh participated in a tournament comprising of eight rounds. In each round, they formed two pairs, with each of them being in exactly one pair. The only restriction in the pairing was that the pairs would change in successive rounds. For example, if Pulak formed a pair with Qasim in the first round, then he would have to form a pair with Ritesh or Suresh in the second round. He would be free to pair with Qasim again in the third round. In each round, each pair decided whether to play the game in that round or not. If they decided not to play, then no money was exchanged between them. If they decided to play, they had to bet either ₹1 or ₹2 in that round. For example, if they chose to bet ₹2, then the player winning the game got ₹2 from the one losing the game. At the beginning of the tournament, the players had ₹10 each. The following table shows partial information about the amounts that the players had at the end of each of the eight rounds. It shows every time a player had ₹10 at the end of a round, as well as every time, at the end of a round, a player had either the minimum or the maximum amount that he would have had across the eight rounds. For example, Suresh had ₹10 at the end of Rounds 1, 3, and 8 and not after any of the other rounds. The maximum amount that he had at the end of any round was ₹13 (at the end of Round 5), and the minimum amount he had at the end of any round was ₹8 (at the end of Round 2). At the end of all other rounds, he must have had either ₹9, ₹11, or ₹12.
It was also known that Pulak and Qasim had the same amount of money with them at the end of Round 4.

Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
There are only four neighbourhoods in a city - Levmisto, Tyhrmisto, Pesmisto and Kitmisto. During the onset of a pandemic, the number of new cases of a disease in each of these neighbourhoods was recorded over a period of five days. On each day, the number of new cases recorded in any of the neighbourhoods was either 0, 1, 2 or 3.
The following facts are also known:
1. There was at least one new case in every neighbourhood on Day 1.
2. On each of the five days, there were more new cases in Kitmisto than in Pesmisto.
3. The number of new cases in the city in a day kept increasing during the five-day period. The number of new cases on Day 3 was exactly one more than that on Day 2.
4. The maximum number of new cases in a day in Pesmisto was 2, and this happened only once during the five-day period.
5. Kitmisto is the only place to have 3 new cases on Day 2.
6. The total numbers of new cases in Levmisto, Tyhrmisto, Pesmisto and Kitmisto over the five-day period were 12, 12, 5 and 14 respectively.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
There are only four neighbourhoods in a city - Levmisto, Tyhrmisto, Pesmisto and Kitmisto. During the onset of a pandemic, the number of new cases of a disease in each of these neighbourhoods was recorded over a period of five days. On each day, the number of new cases recorded in any of the neighbourhoods was either 0, 1, 2 or 3.
The following facts are also known:
1. There was at least one new case in every neighbourhood on Day 1.
2. On each of the five days, there were more new cases in Kitmisto than in Pesmisto.
3. The number of new cases in the city in a day kept increasing during the five-day period. The number of new cases on Day 3 was exactly one more than that on Day 2.
4. The maximum number of new cases in a day in Pesmisto was 2, and this happened only once during the five-day period.
5. Kitmisto is the only place to have 3 new cases on Day 2.
6. The total numbers of new cases in Levmisto, Tyhrmisto, Pesmisto and Kitmisto over the five-day period were 12, 12, 5 and 14 respectively.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
There are only four neighbourhoods in a city - Levmisto, Tyhrmisto, Pesmisto and Kitmisto. During the onset of a pandemic, the number of new cases of a disease in each of these neighbourhoods was recorded over a period of five days. On each day, the number of new cases recorded in any of the neighbourhoods was either 0, 1, 2 or 3.
The following facts are also known:
1. There was at least one new case in every neighbourhood on Day 1.
2. On each of the five days, there were more new cases in Kitmisto than in Pesmisto.
3. The number of new cases in the city in a day kept increasing during the five-day period. The number of new cases on Day 3 was exactly one more than that on Day 2.
4. The maximum number of new cases in a day in Pesmisto was 2, and this happened only once during the five-day period.
5. Kitmisto is the only place to have 3 new cases on Day 2.
6. The total numbers of new cases in Levmisto, Tyhrmisto, Pesmisto and Kitmisto over the five-day period were 12, 12, 5 and 14 respectively.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
There are only four neighbourhoods in a city - Levmisto, Tyhrmisto, Pesmisto and Kitmisto. During the onset of a pandemic, the number of new cases of a disease in each of these neighbourhoods was recorded over a period of five days. On each day, the number of new cases recorded in any of the neighbourhoods was either 0, 1, 2 or 3.
The following facts are also known:
1. There was at least one new case in every neighbourhood on Day 1.
2. On each of the five days, there were more new cases in Kitmisto than in Pesmisto.
3. The number of new cases in the city in a day kept increasing during the five-day period. The number of new cases on Day 3 was exactly one more than that on Day 2.
4. The maximum number of new cases in a day in Pesmisto was 2, and this happened only once during the five-day period.
5. Kitmisto is the only place to have 3 new cases on Day 2.
6. The total numbers of new cases in Levmisto, Tyhrmisto, Pesmisto and Kitmisto over the five-day period were 12, 12, 5 and 14 respectively.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
There are only four neighbourhoods in a city - Levmisto, Tyhrmisto, Pesmisto and Kitmisto. During the onset of a pandemic, the number of new cases of a disease in each of these neighbourhoods was recorded over a period of five days. On each day, the number of new cases recorded in any of the neighbourhoods was either 0, 1, 2 or 3.
The following facts are also known:
1. There was at least one new case in every neighbourhood on Day 1.
2. On each of the five days, there were more new cases in Kitmisto than in Pesmisto.
3. The number of new cases in the city in a day kept increasing during the five-day period. The number of new cases on Day 3 was exactly one more than that on Day 2.
4. The maximum number of new cases in a day in Pesmisto was 2, and this happened only once during the five-day period.
5. Kitmisto is the only place to have 3 new cases on Day 2.
6. The total numbers of new cases in Levmisto, Tyhrmisto, Pesmisto and Kitmisto over the five-day period were 12, 12, 5 and 14 respectively.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
A journal plans to publish 18 research papers, written by eight authors (A, B, C, D, E, F, G, and H) in four issues of the journal scheduled in January, April, July and October. Each of the research papers was written by exactly one of the eight authors. Five papers were scheduled in each of the first two issues, while four were scheduled in each of the last two issues. Every author wrote at least one paper and at most three papers. The total number of papers written by A, D, G and H was double the total number of papers written by the other four authors. Four of the authors were from India and two each were from Japan and China. Each author belonged to exactly one of the three areas — Manufacturing, Automation and Logistics. Four of the authors were from the Logistics area and two were from the Automation area. As per the journal policy, none of the authors could have more than one paper in any issue of the journal.
The following facts are also known.
- F, an Indian author from the Logistics area, wrote only one paper. It was scheduled in the October issue.
- A was from the Automation area and did not have a paper scheduled in the October issue.
- None of the Indian authors were from the Manufacturing area and none of the Japanese or Chinese authors were from the Automation area.
- A and H were from different countries, but had their papers scheduled in exactly the same issues.
- C and E, both Chinese authors from different areas, had the same number of papers scheduled. Further, E had papers scheduled in consecutive issues of the journal but C did not.
- B, from the Logistics area, had a paper scheduled in the April issue of the journal.
- B and G belonged to the same country. None of their papers were scheduled in the same issue of the journal.
- D, a Japanese author from the Manufacturing area, did not have a paper scheduled in the July issue.
- C and H belonged to different areas.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
A journal plans to publish 18 research papers, written by eight authors (A, B, C, D, E, F, G, and H) in four issues of the journal scheduled in January, April, July and October. Each of the research papers was written by exactly one of the eight authors. Five papers were scheduled in each of the first two issues, while four were scheduled in each of the last two issues. Every author wrote at least one paper and at most three papers. The total number of papers written by A, D, G and H was double the total number of papers written by the other four authors. Four of the authors were from India and two each were from Japan and China. Each author belonged to exactly one of the three areas — Manufacturing, Automation and Logistics. Four of the authors were from the Logistics area and two were from the Automation area. As per the journal policy, none of the authors could have more than one paper in any issue of the journal.
The following facts are also known.
- F, an Indian author from the Logistics area, wrote only one paper. It was scheduled in the October issue.
- A was from the Automation area and did not have a paper scheduled in the October issue.
- None of the Indian authors were from the Manufacturing area and none of the Japanese or Chinese authors were from the Automation area.
- A and H were from different countries, but had their papers scheduled in exactly the same issues.
- C and E, both Chinese authors from different areas, had the same number of papers scheduled. Further, E had papers scheduled in consecutive issues of the journal but C did not.
- B, from the Logistics area, had a paper scheduled in the April issue of the journal.
- B and G belonged to the same country. None of their papers were scheduled in the same issue of the journal.
- D, a Japanese author from the Manufacturing area, did not have a paper scheduled in the July issue.
- C and H belonged to different areas.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
A journal plans to publish 18 research papers, written by eight authors (A, B, C, D, E, F, G, and H) in four issues of the journal scheduled in January, April, July and October. Each of the research papers was written by exactly one of the eight authors. Five papers were scheduled in each of the first two issues, while four were scheduled in each of the last two issues. Every author wrote at least one paper and at most three papers. The total number of papers written by A, D, G and H was double the total number of papers written by the other four authors. Four of the authors were from India and two each were from Japan and China. Each author belonged to exactly one of the three areas — Manufacturing, Automation and Logistics. Four of the authors were from the Logistics area and two were from the Automation area. As per the journal policy, none of the authors could have more than one paper in any issue of the journal.
The following facts are also known.
- F, an Indian author from the Logistics area, wrote only one paper. It was scheduled in the October issue.
- A was from the Automation area and did not have a paper scheduled in the October issue.
- None of the Indian authors were from the Manufacturing area and none of the Japanese or Chinese authors were from the Automation area.
- A and H were from different countries, but had their papers scheduled in exactly the same issues.
- C and E, both Chinese authors from different areas, had the same number of papers scheduled. Further, E had papers scheduled in consecutive issues of the journal but C did not.
- B, from the Logistics area, had a paper scheduled in the April issue of the journal.
- B and G belonged to the same country. None of their papers were scheduled in the same issue of the journal.
- D, a Japanese author from the Manufacturing area, did not have a paper scheduled in the July issue.
- C and H belonged to different areas.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
A journal plans to publish 18 research papers, written by eight authors (A, B, C, D, E, F, G, and H) in four issues of the journal scheduled in January, April, July and October. Each of the research papers was written by exactly one of the eight authors. Five papers were scheduled in each of the first two issues, while four were scheduled in each of the last two issues. Every author wrote at least one paper and at most three papers. The total number of papers written by A, D, G and H was double the total number of papers written by the other four authors. Four of the authors were from India and two each were from Japan and China. Each author belonged to exactly one of the three areas — Manufacturing, Automation and Logistics. Four of the authors were from the Logistics area and two were from the Automation area. As per the journal policy, none of the authors could have more than one paper in any issue of the journal.
The following facts are also known.
- F, an Indian author from the Logistics area, wrote only one paper. It was scheduled in the October issue.
- A was from the Automation area and did not have a paper scheduled in the October issue.
- None of the Indian authors were from the Manufacturing area and none of the Japanese or Chinese authors were from the Automation area.
- A and H were from different countries, but had their papers scheduled in exactly the same issues.
- C and E, both Chinese authors from different areas, had the same number of papers scheduled. Further, E had papers scheduled in consecutive issues of the journal but C did not.
- B, from the Logistics area, had a paper scheduled in the April issue of the journal.
- B and G belonged to the same country. None of their papers were scheduled in the same issue of the journal.
- D, a Japanese author from the Manufacturing area, did not have a paper scheduled in the July issue.
- C and H belonged to different areas.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
A journal plans to publish 18 research papers, written by eight authors (A, B, C, D, E, F, G, and H) in four issues of the journal scheduled in January, April, July and October. Each of the research papers was written by exactly one of the eight authors. Five papers were scheduled in each of the first two issues, while four were scheduled in each of the last two issues. Every author wrote at least one paper and at most three papers. The total number of papers written by A, D, G and H was double the total number of papers written by the other four authors. Four of the authors were from India and two each were from Japan and China. Each author belonged to exactly one of the three areas — Manufacturing, Automation and Logistics. Four of the authors were from the Logistics area and two were from the Automation area. As per the journal policy, none of the authors could have more than one paper in any issue of the journal.
The following facts are also known.
- F, an Indian author from the Logistics area, wrote only one paper. It was scheduled in the October issue.
- A was from the Automation area and did not have a paper scheduled in the October issue.
- None of the Indian authors were from the Manufacturing area and none of the Japanese or Chinese authors were from the Automation area.
- A and H were from different countries, but had their papers scheduled in exactly the same issues.
- C and E, both Chinese authors from different areas, had the same number of papers scheduled. Further, E had papers scheduled in consecutive issues of the journal but C did not.
- B, from the Logistics area, had a paper scheduled in the April issue of the journal.
- B and G belonged to the same country. None of their papers were scheduled in the same issue of the journal.
- D, a Japanese author from the Manufacturing area, did not have a paper scheduled in the July issue.
- C and H belonged to different areas.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
A journal plans to publish 18 research papers, written by eight authors (A, B, C, D, E, F, G, and H) in four issues of the journal scheduled in January, April, July and October. Each of the research papers was written by exactly one of the eight authors. Five papers were scheduled in each of the first two issues, while four were scheduled in each of the last two issues. Every author wrote at least one paper and at most three papers. The total number of papers written by A, D, G and H was double the total number of papers written by the other four authors. Four of the authors were from India and two each were from Japan and China. Each author belonged to exactly one of the three areas — Manufacturing, Automation and Logistics. Four of the authors were from the Logistics area and two were from the Automation area. As per the journal policy, none of the authors could have more than one paper in any issue of the journal.
The following facts are also known.
- F, an Indian author from the Logistics area, wrote only one paper. It was scheduled in the October issue.
- A was from the Automation area and did not have a paper scheduled in the October issue.
- None of the Indian authors were from the Manufacturing area and none of the Japanese or Chinese authors were from the Automation area.
- A and H were from different countries, but had their papers scheduled in exactly the same issues.
- C and E, both Chinese authors from different areas, had the same number of papers scheduled. Further, E had papers scheduled in consecutive issues of the journal but C did not.
- B, from the Logistics area, had a paper scheduled in the April issue of the journal.
- B and G belonged to the same country. None of their papers were scheduled in the same issue of the journal.
- D, a Japanese author from the Manufacturing area, did not have a paper scheduled in the July issue.
- C and H belonged to different areas.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
Four institutes, A, B, C, and D, had contracts with four vendors W, X, Y, and Z during the ten calendar years from 2010 to 2019. The contracts were either multi-year contracts running for several consecutive years or single-year contracts. No institute had more than one contract with the same vendor. However, in a calendar year, an institute may have had contracts with multiple vendors, and a vendor may have had contracts with multiple institutes. It is known that over the decade, the institutes each got into two contracts with two of these vendors, and each vendor got into two contracts with two of these institutes.
The following facts are also known about these contracts.
I. Vendor Z had at least one contract in every year.
II. Vendor X had one or more contracts in every year up to 2015, but no contract in any year after that.
III. Vendor Y had contracts in 2010 and 2019. Vendor W had contracts only in 2012.
IV. There were five contracts in 2012.
V. There were exactly four multi-year contracts. Institute B had a 7-year contract, D had a 4-year contract, and A and C had one 3-year contract each. The other four contracts were single-year contracts.
VI. Institute C had one or more contracts in 2012 but did not have any contract in 2011.
VII. Institutes B and D each had exactly one contract in 2012. Institute D did not have any contract in 2010.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
Four institutes, A, B, C, and D, had contracts with four vendors W, X, Y, and Z during the ten calendar years from 2010 to 2019. The contracts were either multi-year contracts running for several consecutive years or single-year contracts. No institute had more than one contract with the same vendor. However, in a calendar year, an institute may have had contracts with multiple vendors, and a vendor may have had contracts with multiple institutes. It is known that over the decade, the institutes each got into two contracts with two of these vendors, and each vendor got into two contracts with two of these institutes.
The following facts are also known about these contracts.
I. Vendor Z had at least one contract in every year.
II. Vendor X had one or more contracts in every year up to 2015, but no contract in any year after that.
III. Vendor Y had contracts in 2010 and 2019. Vendor W had contracts only in 2012.
IV. There were five contracts in 2012.
V. There were exactly four multi-year contracts. Institute B had a 7-year contract, D had a 4-year contract, and A and C had one 3-year contract each. The other four contracts were single-year contracts.
VI. Institute C had one or more contracts in 2012 but did not have any contract in 2011.
VII. Institutes B and D each had exactly one contract in 2012. Institute D did not have any contract in 2010.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
Four institutes, A, B, C, and D, had contracts with four vendors W, X, Y, and Z during the ten calendar years from 2010 to 2019. The contracts were either multi-year contracts running for several consecutive years or single-year contracts. No institute had more than one contract with the same vendor. However, in a calendar year, an institute may have had contracts with multiple vendors, and a vendor may have had contracts with multiple institutes. It is known that over the decade, the institutes each got into two contracts with two of these vendors, and each vendor got into two contracts with two of these institutes.
The following facts are also known about these contracts.
I. Vendor Z had at least one contract in every year.
II. Vendor X had one or more contracts in every year up to 2015, but no contract in any year after that.
III. Vendor Y had contracts in 2010 and 2019. Vendor W had contracts only in 2012.
IV. There were five contracts in 2012.
V. There were exactly four multi-year contracts. Institute B had a 7-year contract, D had a 4-year contract, and A and C had one 3-year contract each. The other four contracts were single-year contracts.
VI. Institute C had one or more contracts in 2012 but did not have any contract in 2011.
VII. Institutes B and D each had exactly one contract in 2012. Institute D did not have any contract in 2010.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
Four institutes, A, B, C, and D, had contracts with four vendors W, X, Y, and Z during the ten calendar years from 2010 to 2019. The contracts were either multi-year contracts running for several consecutive years or single-year contracts. No institute had more than one contract with the same vendor. However, in a calendar year, an institute may have had contracts with multiple vendors, and a vendor may have had contracts with multiple institutes. It is known that over the decade, the institutes each got into two contracts with two of these vendors, and each vendor got into two contracts with two of these institutes.
The following facts are also known about these contracts.
I. Vendor Z had at least one contract in every year.
II. Vendor X had one or more contracts in every year up to 2015, but no contract in any year after that.
III. Vendor Y had contracts in 2010 and 2019. Vendor W had contracts only in 2012.
IV. There were five contracts in 2012.
V. There were exactly four multi-year contracts. Institute B had a 7-year contract, D had a 4-year contract, and A and C had one 3-year contract each. The other four contracts were single-year contracts.
VI. Institute C had one or more contracts in 2012 but did not have any contract in 2011.
VII. Institutes B and D each had exactly one contract in 2012. Institute D did not have any contract in 2010.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
Four institutes, A, B, C, and D, had contracts with four vendors W, X, Y, and Z during the ten calendar years from 2010 to 2019. The contracts were either multi-year contracts running for several consecutive years or single-year contracts. No institute had more than one contract with the same vendor. However, in a calendar year, an institute may have had contracts with multiple vendors, and a vendor may have had contracts with multiple institutes. It is known that over the decade, the institutes each got into two contracts with two of these vendors, and each vendor got into two contracts with two of these institutes.
The following facts are also known about these contracts.
I. Vendor Z had at least one contract in every year.
II. Vendor X had one or more contracts in every year up to 2015, but no contract in any year after that.
III. Vendor Y had contracts in 2010 and 2019. Vendor W had contracts only in 2012.
IV. There were five contracts in 2012.
V. There were exactly four multi-year contracts. Institute B had a 7-year contract, D had a 4-year contract, and A and C had one 3-year contract each. The other four contracts were single-year contracts.
VI. Institute C had one or more contracts in 2012 but did not have any contract in 2011.
VII. Institutes B and D each had exactly one contract in 2012. Institute D did not have any contract in 2010.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
Four institutes, A, B, C, and D, had contracts with four vendors W, X, Y, and Z during the ten calendar years from 2010 to 2019. The contracts were either multi-year contracts running for several consecutive years or single-year contracts. No institute had more than one contract with the same vendor. However, in a calendar year, an institute may have had contracts with multiple vendors, and a vendor may have had contracts with multiple institutes. It is known that over the decade, the institutes each got into two contracts with two of these vendors, and each vendor got into two contracts with two of these institutes.
The following facts are also known about these contracts.
I. Vendor Z had at least one contract in every year.
II. Vendor X had one or more contracts in every year up to 2015, but no contract in any year after that.
III. Vendor Y had contracts in 2010 and 2019. Vendor W had contracts only in 2012.
IV. There were five contracts in 2012.
V. There were exactly four multi-year contracts. Institute B had a 7-year contract, D had a 4-year contract, and A and C had one 3-year contract each. The other four contracts were single-year contracts.
VI. Institute C had one or more contracts in 2012 but did not have any contract in 2011.
VII. Institutes B and D each had exactly one contract in 2012. Institute D did not have any contract in 2010.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
Ten musicians (A, B, C, D, E, F, G, H, I and J) are experts in at least one of the following three percussion instruments: tabla, mridangam, and ghatam. Among them, three are experts in tabla but not in mridangam or ghatam, another three are experts in mridangam but not in tabla or ghatam, and one is an expert in ghatam but not in tabla or mridangam. Further, two are experts in tabla and mridangam but not in ghatam, and one is an expert in tabla and ghatam but not in mridangam.
The following facts are known about these ten musicians.
1. Both A and B are experts in mridangam, but only one of them is also an expert in tabla.
2. D is an expert in both tabla and ghatam.
3. Both F and G are experts in tabla, but only one of them is also an expert in mridangam.
4. Neither I nor J is an expert in tabla.
5. Neither H nor I is an expert in mridangam, but only one of them is an expert in ghatam.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
Ten musicians (A, B, C, D, E, F, G, H, I and J) are experts in at least one of the following three percussion instruments: tabla, mridangam, and ghatam. Among them, three are experts in tabla but not in mridangam or ghatam, another three are experts in mridangam but not in tabla or ghatam, and one is an expert in ghatam but not in tabla or mridangam. Further, two are experts in tabla and mridangam but not in ghatam, and one is an expert in tabla and ghatam but not in mridangam.
The following facts are known about these ten musicians.
1. Both A and B are experts in mridangam, but only one of them is also an expert in tabla.
2. D is an expert in both tabla and ghatam.
3. Both F and G are experts in tabla, but only one of them is also an expert in mridangam.
4. Neither I nor J is an expert in tabla.
5. Neither H nor I is an expert in mridangam, but only one of them is an expert in ghatam.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
Ten musicians (A, B, C, D, E, F, G, H, I and J) are experts in at least one of the following three percussion instruments: tabla, mridangam, and ghatam. Among them, three are experts in tabla but not in mridangam or ghatam, another three are experts in mridangam but not in tabla or ghatam, and one is an expert in ghatam but not in tabla or mridangam. Further, two are experts in tabla and mridangam but not in ghatam, and one is an expert in tabla and ghatam but not in mridangam.
The following facts are known about these ten musicians.
1. Both A and B are experts in mridangam, but only one of them is also an expert in tabla.
2. D is an expert in both tabla and ghatam.
3. Both F and G are experts in tabla, but only one of them is also an expert in mridangam.
4. Neither I nor J is an expert in tabla.
5. Neither H nor I is an expert in mridangam, but only one of them is an expert in ghatam.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
Ten musicians (A, B, C, D, E, F, G, H, I and J) are experts in at least one of the following three percussion instruments: tabla, mridangam, and ghatam. Among them, three are experts in tabla but not in mridangam or ghatam, another three are experts in mridangam but not in tabla or ghatam, and one is an expert in ghatam but not in tabla or mridangam. Further, two are experts in tabla and mridangam but not in ghatam, and one is an expert in tabla and ghatam but not in mridangam.
The following facts are known about these ten musicians.
1. Both A and B are experts in mridangam, but only one of them is also an expert in tabla.
2. D is an expert in both tabla and ghatam.
3. Both F and G are experts in tabla, but only one of them is also an expert in mridangam.
4. Neither I nor J is an expert in tabla.
5. Neither H nor I is an expert in mridangam, but only one of them is an expert in ghatam.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
1000 patients currently suffering from a disease were selected to study the effectiveness of treatment of four types of medicines — A, B, C and D. These patients were first randomly assigned into two groups of equal size, called treatment group and control group. The patients in the control group were not treated with any of these medicines; instead they were given a dummy medicine, called placebo, containing only sugar and starch.
The following information is known about the patients in the treatment group.
A. A total of 250 patients were treated with type A medicine and a total of 210 patients were treated with type C medicine.
B. 25 patients were treated with type A medicine only. 20 patients were treated with type C medicine only. 10 patients were treated with type D medicine only.
C. 35 patients were treated with type A and type D medicines only. 20 patients were treated with type A and type B medicines only. 30 patients were treated with type A and type C medicines only. 20 patients were treated with type C and type D medicines only.
D. 100 patients were treated with exactly three types of medicines.
E. 40 patients were treated with medicines of types A, B and C, but not with medicines of type D. 20 patients were treated with medicines of types A, C and D, but not with medicines of type B.
F. 50 patients were given all the four types of medicines. 75 patients were treated with exactly one type of medicine.
340
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
1000 patients currently suffering from a disease were selected to study the effectiveness of treatment of four types of medicines — A, B, C and D. These patients were first randomly assigned into two groups of equal size, called treatment group and control group. The patients in the control group were not treated with any of these medicines; instead they were given a dummy medicine, called placebo, containing only sugar and starch.
The following information is known about the patients in the treatment group.
A. A total of 250 patients were treated with type A medicine and a total of 210 patients were treated with type C medicine.
B. 25 patients were treated with type A medicine only. 20 patients were treated with type C medicine only. 10 patients were treated with type D medicine only.
C. 35 patients were treated with type A and type D medicines only. 20 patients were treated with type A and type B medicines only. 30 patients were treated with type A and type C medicines only. 20 patients were treated with type C and type D medicines only.
D. 100 patients were treated with exactly three types of medicines.
E. 40 patients were treated with medicines of types A, B and C, but not with medicines of type D. 20 patients were treated with medicines of types A, C and D, but not with medicines of type B.
F. 50 patients were given all the four types of medicines. 75 patients were treated with exactly one type of medicine.
CAT/2020.1(DILR)
Question. 58
The number of patients who were treated with medicine types B, C and D, but not type A was:
10
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
1000 patients currently suffering from a disease were selected to study the effectiveness of treatment of four types of medicines — A, B, C and D. These patients were first randomly assigned into two groups of equal size, called treatment group and control group. The patients in the control group were not treated with any of these medicines; instead they were given a dummy medicine, called placebo, containing only sugar and starch.
The following information is known about the patients in the treatment group.
A. A total of 250 patients were treated with type A medicine and a total of 210 patients were treated with type C medicine.
B. 25 patients were treated with type A medicine only. 20 patients were treated with type C medicine only. 10 patients were treated with type D medicine only.
C. 35 patients were treated with type A and type D medicines only. 20 patients were treated with type A and type B medicines only. 30 patients were treated with type A and type C medicines only. 20 patients were treated with type C and type D medicines only.
D. 100 patients were treated with exactly three types of medicines.
E. 40 patients were treated with medicines of types A, B and C, but not with medicines of type D. 20 patients were treated with medicines of types A, C and D, but not with medicines of type B.
F. 50 patients were given all the four types of medicines. 75 patients were treated with exactly one type of medicine.
150
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
1000 patients currently suffering from a disease were selected to study the effectiveness of treatment of four types of medicines — A, B, C and D. These patients were first randomly assigned into two groups of equal size, called treatment group and control group. The patients in the control group were not treated with any of these medicines; instead they were given a dummy medicine, called placebo, containing only sugar and starch.
The following information is known about the patients in the treatment group.
A. A total of 250 patients were treated with type A medicine and a total of 210 patients were treated with type C medicine.
B. 25 patients were treated with type A medicine only. 20 patients were treated with type C medicine only. 10 patients were treated with type D medicine only.
C. 35 patients were treated with type A and type D medicines only. 20 patients were treated with type A and type B medicines only. 30 patients were treated with type A and type C medicines only. 20 patients were treated with type C and type D medicines only.
D. 100 patients were treated with exactly three types of medicines.
E. 40 patients were treated with medicines of types A, B and C, but not with medicines of type D. 20 patients were treated with medicines of types A, C and D, but not with medicines of type B.
F. 50 patients were given all the four types of medicines. 75 patients were treated with exactly one type of medicine.
325
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Twenty five coloured beads are to be arranged in a grid comprising of five rows and five columns. Each cell in the grid must contain exactly one bead. Each bead is coloured either Red, Blue or Green.
While arranging the beads along any of the five rows or along any of the five columns, the rules given below are to be followed:
1. Two adjacent beads along the same row or column are always of different colours.
2. There is at least one Green bead between any two Blue beads along the same row or column.
3. There is at least one Blue and at least one Green bead between any two Red beads along the same row or column.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Twenty five coloured beads are to be arranged in a grid comprising of five rows and five columns. Each cell in the grid must contain exactly one bead. Each bead is coloured either Red, Blue or Green.
While arranging the beads along any of the five rows or along any of the five columns, the rules given below are to be followed:
1. Two adjacent beads along the same row or column are always of different colours.
2. There is at least one Green bead between any two Blue beads along the same row or column.
3. There is at least one Blue and at least one Green bead between any two Red beads along the same row or column.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Twenty five coloured beads are to be arranged in a grid comprising of five rows and five columns. Each cell in the grid must contain exactly one bead. Each bead is coloured either Red, Blue or Green.
While arranging the beads along any of the five rows or along any of the five columns, the rules given below are to be followed:
1. Two adjacent beads along the same row or column are always of different colours.
2. There is at least one Green bead between any two Blue beads along the same row or column.
3. There is at least one Blue and at least one Green bead between any two Red beads along the same row or column.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Twenty five coloured beads are to be arranged in a grid comprising of five rows and five columns. Each cell in the grid must contain exactly one bead. Each bead is coloured either Red, Blue or Green.
While arranging the beads along any of the five rows or along any of the five columns, the rules given below are to be followed:
1. Two adjacent beads along the same row or column are always of different colours.
2. There is at least one Green bead between any two Blue beads along the same row or column.
3. There is at least one Blue and at least one Green bead between any two Red beads along the same row or column.
Comprehension
A shopping mall has a large basement parking lot with parking slots painted in it along a single row. These slots are quite narrow; a compact car can fit in a single slot but an SUV requires two slots. When a car arrives, the parking attendant guides the car to the first available slot from the beginning of the row into which the car can fit.
For our purpose, cars are numbered according to the order in which they arrive at the lot. For example, the first car to arrive is given a number 1, the second a number 2, and so on. This numbering does not indicate whether a car is a compact or an SUV. The configuration of a parking lot is a sequence of the car numbers in each slot. Each single vacant slot is represented by letter V.
For instance, suppose cars numbered 1 through 5 arrive and park, where cars 1,3 and 5 are compact cars and 2 and 4 are SUVs. At this point, the parking lot would be described by the sequence 1, 2, 3, 4, 5. If cars 2 and 5 now vacate their slots, the parking lot would now be described as 1, V, V, 3, 4. If a compact car (numbered 6) arrives subsequently followed by an SUV (numbered 7), the parking lot would be described by the sequence 1, 6, V, 3, 4, 7.
Answer the following questions INDEPENDENTLY of each other.
CAT/2020.2(DILR)
Question. 65
Initially, cars numbered 1, 2, 3, and 4 arrive among which 1 and 4 are SUVs while 2 and 3 are compact cars. Car 1 then leaves, followed by the arrivals of car 5 (a compact car) and car 6 (an SUV). Car 4 then leaves. Then car 7 (an SUV) and car 8 (a compact car) arrive. At this moment, which among the following numbered car is parked next to car 3?
Comprehension
A shopping mall has a large basement parking lot with parking slots painted in it along a single row. These slots are quite narrow; a compact car can fit in a single slot but an SUV requires two slots. When a car arrives, the parking attendant guides the car to the first available slot from the beginning of the row into which the car can fit.
For our purpose, cars are numbered according to the order in which they arrive at the lot. For example, the first car to arrive is given a number 1, the second a number 2, and so on. This numbering does not indicate whether a car is a compact or an SUV. The configuration of a parking lot is a sequence of the car numbers in each slot. Each single vacant slot is represented by letter V.
For instance, suppose cars numbered 1 through 5 arrive and park, where cars 1,3 and 5 are compact cars and 2 and 4 are SUVs. At this point, the parking lot would be described by the sequence 1, 2, 3, 4, 5. If cars 2 and 5 now vacate their slots, the parking lot would now be described as 1, V, V, 3, 4. If a compact car (numbered 6) arrives subsequently followed by an SUV (numbered 7), the parking lot would be described by the sequence 1, 6, V, 3, 4, 7.
Answer the following questions INDEPENDENTLY of each other.
Comprehension
A shopping mall has a large basement parking lot with parking slots painted in it along a single row. These slots are quite narrow; a compact car can fit in a single slot but an SUV requires two slots. When a car arrives, the parking attendant guides the car to the first available slot from the beginning of the row into which the car can fit.
For our purpose, cars are numbered according to the order in which they arrive at the lot. For example, the first car to arrive is given a number 1, the second a number 2, and so on. This numbering does not indicate whether a car is a compact or an SUV. The configuration of a parking lot is a sequence of the car numbers in each slot. Each single vacant slot is represented by letter V.
For instance, suppose cars numbered 1 through 5 arrive and park, where cars 1,3 and 5 are compact cars and 2 and 4 are SUVs. At this point, the parking lot would be described by the sequence 1, 2, 3, 4, 5. If cars 2 and 5 now vacate their slots, the parking lot would now be described as 1, V, V, 3, 4. If a compact car (numbered 6) arrives subsequently followed by an SUV (numbered 7), the parking lot would be described by the sequence 1, 6, V, 3, 4, 7.
Answer the following questions INDEPENDENTLY of each other.
Comprehension
A shopping mall has a large basement parking lot with parking slots painted in it along a single row. These slots are quite narrow; a compact car can fit in a single slot but an SUV requires two slots. When a car arrives, the parking attendant guides the car to the first available slot from the beginning of the row into which the car can fit.
For our purpose, cars are numbered according to the order in which they arrive at the lot. For example, the first car to arrive is given a number 1, the second a number 2, and so on. This numbering does not indicate whether a car is a compact or an SUV. The configuration of a parking lot is a sequence of the car numbers in each slot. Each single vacant slot is represented by letter V.
For instance, suppose cars numbered 1 through 5 arrive and park, where cars 1,3 and 5 are compact cars and 2 and 4 are SUVs. At this point, the parking lot would be described by the sequence 1, 2, 3, 4, 5. If cars 2 and 5 now vacate their slots, the parking lot would now be described as 1, V, V, 3, 4. If a compact car (numbered 6) arrives subsequently followed by an SUV (numbered 7), the parking lot would be described by the sequence 1, 6, V, 3, 4, 7.
Answer the following questions INDEPENDENTLY of each other.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
A survey of 600 schools in India was conducted to gather information about their online teaching learning processes (OTLP).
The following four facilities were studied.
F1: Own software for OTLP
F2: Trained teachers for OTLP
F3: Training materials for OTLP
F4: All students having Laptops
The following observations were summarized from the survey.
1. 80 schools did not have any of the four facilities – F1, F2, F3, F4.
2. 40 schools had all four facilities.
3. The number of schools with only F1, only F2, only F3, and only F4 was 25, 30, 26 and 20 respectively.
4. The number of schools with exactly three of the facilities was the same irrespective of which three were considered.
5. 313 schools had F2.
6. 26 schools had only F2 and F3 (but neither F1 nor F4).
7. Among the schools having F4, 24 had only F3, and 45 had only F2.
8. 162 schools had both F1 and F2.
9. The number of schools having F1 was the same as the number of schools having F4.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
A survey of 600 schools in India was conducted to gather information about their online teaching learning processes (OTLP).
The following four facilities were studied.
F1: Own software for OTLP
F2: Trained teachers for OTLP
F3: Training materials for OTLP
F4: All students having Laptops
The following observations were summarized from the survey.
1. 80 schools did not have any of the four facilities – F1, F2, F3, F4.
2. 40 schools had all four facilities.
3. The number of schools with only F1, only F2, only F3, and only F4 was 25, 30, 26 and 20 respectively.
4. The number of schools with exactly three of the facilities was the same irrespective of which three were considered.
5. 313 schools had F2.
6. 26 schools had only F2 and F3 (but neither F1 nor F4).
7. Among the schools having F4, 24 had only F3, and 45 had only F2.
8. 162 schools had both F1 and F2.
9. The number of schools having F1 was the same as the number of schools having F4.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
A survey of 600 schools in India was conducted to gather information about their online teaching learning processes (OTLP).
The following four facilities were studied.
F1: Own software for OTLP
F2: Trained teachers for OTLP
F3: Training materials for OTLP
F4: All students having Laptops
The following observations were summarized from the survey.
1. 80 schools did not have any of the four facilities – F1, F2, F3, F4.
2. 40 schools had all four facilities.
3. The number of schools with only F1, only F2, only F3, and only F4 was 25, 30, 26 and 20 respectively.
4. The number of schools with exactly three of the facilities was the same irrespective of which three were considered.
5. 313 schools had F2.
6. 26 schools had only F2 and F3 (but neither F1 nor F4).
7. Among the schools having F4, 24 had only F3, and 45 had only F2.
8. 162 schools had both F1 and F2.
9. The number of schools having F1 was the same as the number of schools having F4.
42
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
A survey of 600 schools in India was conducted to gather information about their online teaching learning processes (OTLP).
The following four facilities were studied.
F1: Own software for OTLP
F2: Trained teachers for OTLP
F3: Training materials for OTLP
F4: All students having Laptops
The following observations were summarized from the survey.
1. 80 schools did not have any of the four facilities – F1, F2, F3, F4.
2. 40 schools had all four facilities.
3. The number of schools with only F1, only F2, only F3, and only F4 was 25, 30, 26 and 20 respectively.
4. The number of schools with exactly three of the facilities was the same irrespective of which three were considered.
5. 313 schools had F2.
6. 26 schools had only F2 and F3 (but neither F1 nor F4).
7. Among the schools having F4, 24 had only F3, and 45 had only F2.
8. 162 schools had both F1 and F2.
9. The number of schools having F1 was the same as the number of schools having F4.
20
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
A supermarket has to place 12 items (coded A to L) in shelves numbered 1 to 16. Five of these items are types of biscuits, three are types of candies and the rest are types of savouries. Only one item can be kept in a shelf. Items are to be placed such that all items of same type are clustered together with no empty shelf between items of the same type and at least one empty shelf between two different types of items. At most two empty shelves can have consecutive numbers.
The following additional facts are known.
1. A and B are to be placed in consecutively numbered shelves in increasing order.
2. I and J are to be placed in consecutively numbered shelves both higher numbered than the shelves in which A and B are kept.
3. D, E and F are savouries and are to be placed in consecutively numbered shelves in increasing order after all the biscuits and candies.
4. K is to be placed in shelf number 16.
5. L and J are items of the same type, while H is an item of a different type.
6. C is a candy and is to be placed in a shelf preceded by two empty shelves.
7. L is to be placed in a shelf preceded by exactly one empty shelf.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
A supermarket has to place 12 items (coded A to L) in shelves numbered 1 to 16. Five of these items are types of biscuits, three are types of candies and the rest are types of savouries. Only one item can be kept in a shelf. Items are to be placed such that all items of same type are clustered together with no empty shelf between items of the same type and at least one empty shelf between two different types of items. At most two empty shelves can have consecutive numbers.
The following additional facts are known.
1. A and B are to be placed in consecutively numbered shelves in increasing order.
2. I and J are to be placed in consecutively numbered shelves both higher numbered than the shelves in which A and B are kept.
3. D, E and F are savouries and are to be placed in consecutively numbered shelves in increasing order after all the biscuits and candies.
4. K is to be placed in shelf number 16.
5. L and J are items of the same type, while H is an item of a different type.
6. C is a candy and is to be placed in a shelf preceded by two empty shelves.
7. L is to be placed in a shelf preceded by exactly one empty shelf.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
A supermarket has to place 12 items (coded A to L) in shelves numbered 1 to 16. Five of these items are types of biscuits, three are types of candies and the rest are types of savouries. Only one item can be kept in a shelf. Items are to be placed such that all items of same type are clustered together with no empty shelf between items of the same type and at least one empty shelf between two different types of items. At most two empty shelves can have consecutive numbers.
The following additional facts are known.
1. A and B are to be placed in consecutively numbered shelves in increasing order.
2. I and J are to be placed in consecutively numbered shelves both higher numbered than the shelves in which A and B are kept.
3. D, E and F are savouries and are to be placed in consecutively numbered shelves in increasing order after all the biscuits and candies.
4. K is to be placed in shelf number 16.
5. L and J are items of the same type, while H is an item of a different type.
6. C is a candy and is to be placed in a shelf preceded by two empty shelves.
7. L is to be placed in a shelf preceded by exactly one empty shelf.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
A supermarket has to place 12 items (coded A to L) in shelves numbered 1 to 16. Five of these items are types of biscuits, three are types of candies and the rest are types of savouries. Only one item can be kept in a shelf. Items are to be placed such that all items of same type are clustered together with no empty shelf between items of the same type and at least one empty shelf between two different types of items. At most two empty shelves can have consecutive numbers.
The following additional facts are known.
1. A and B are to be placed in consecutively numbered shelves in increasing order.
2. I and J are to be placed in consecutively numbered shelves both higher numbered than the shelves in which A and B are kept.
3. D, E and F are savouries and are to be placed in consecutively numbered shelves in increasing order after all the biscuits and candies.
4. K is to be placed in shelf number 16.
5. L and J are items of the same type, while H is an item of a different type.
6. C is a candy and is to be placed in a shelf preceded by two empty shelves.
7. L is to be placed in a shelf preceded by exactly one empty shelf.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
The following table represents addition of two six-digit numbers given in the first and the second rows, while the sum is given in the third row. In the representation, each of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 has been coded with one letter among A, B, C, D, E, F, G, H, J, K, with distinct letters representing distinct digits.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
The following table represents addition of two six-digit numbers given in the first and the second rows, while the sum is given in the third row. In the representation, each of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 has been coded with one letter among A, B, C, D, E, F, G, H, J, K, with distinct letters representing distinct digits.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
The following table represents addition of two six-digit numbers given in the first and the second rows, while the sum is given in the third row. In the representation, each of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 has been coded with one letter among A, B, C, D, E, F, G, H, J, K, with distinct letters representing distinct digits.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
The following table represents addition of two six-digit numbers given in the first and the second rows, while the sum is given in the third row. In the representation, each of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 has been coded with one letter among A, B, C, D, E, F, G, H, J, K, with distinct letters representing distinct digits.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Princess, Queen, Rani, and Samragni were the four finalists in a dance competition. Ashman, Badal, Gagan, and Dyu were the four music composers who individually assigned items to the dancers. Each dancer had to individually perform in two dance items assigned by the different composers. The first items performed by the four dancers were all assigned by different music composers. No dancer performed her second item before the performance of the first item by any other dancers. The dancers performed their second items in the same sequence of their performance of their first items.
The following additional facts are known.
i) No composer who assigned an item to Princess, assigned any item to Queen.
ii) No composer who assigned an item to Rani, assigned any item to Samragni.
iii) The first performance was by Princess; this item was assigned by Badal.
iv) The last performance was by Rani; this item was assigned by Gagan.
v) The items assigned by Ashman were performed consecutively. The number of performances between items assigned by each of the remaining composers was the same.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Princess, Queen, Rani, and Samragni were the four finalists in a dance competition. Ashman, Badal, Gagan, and Dyu were the four music composers who individually assigned items to the dancers. Each dancer had to individually perform in two dance items assigned by the different composers. The first items performed by the four dancers were all assigned by different music composers. No dancer performed her second item before the performance of the first item by any other dancers. The dancers performed their second items in the same sequence of their performance of their first items.
The following additional facts are known.
i) No composer who assigned an item to Princess, assigned any item to Queen.
ii) No composer who assigned an item to Rani, assigned any item to Samragni.
iii) The first performance was by Princess; this item was assigned by Badal.
iv) The last performance was by Rani; this item was assigned by Gagan.
v) The items assigned by Ashman were performed consecutively. The number of performances between items assigned by each of the remaining composers was the same.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Princess, Queen, Rani, and Samragni were the four finalists in a dance competition. Ashman, Badal, Gagan, and Dyu were the four music composers who individually assigned items to the dancers. Each dancer had to individually perform in two dance items assigned by the different composers. The first items performed by the four dancers were all assigned by different music composers. No dancer performed her second item before the performance of the first item by any other dancers. The dancers performed their second items in the same sequence of their performance of their first items.
The following additional facts are known.
i) No composer who assigned an item to Princess, assigned any item to Queen.
ii) No composer who assigned an item to Rani, assigned any item to Samragni.
iii) The first performance was by Princess; this item was assigned by Badal.
iv) The last performance was by Rani; this item was assigned by Gagan.
v) The items assigned by Ashman were performed consecutively. The number of performances between items assigned by each of the remaining composers was the same.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Princess, Queen, Rani, and Samragni were the four finalists in a dance competition. Ashman, Badal, Gagan, and Dyu were the four music composers who individually assigned items to the dancers. Each dancer had to individually perform in two dance items assigned by the different composers. The first items performed by the four dancers were all assigned by different music composers. No dancer performed her second item before the performance of the first item by any other dancers. The dancers performed their second items in the same sequence of their performance of their first items.
The following additional facts are known.
i) No composer who assigned an item to Princess, assigned any item to Queen.
ii) No composer who assigned an item to Rani, assigned any item to Samragni.
iii) The first performance was by Princess; this item was assigned by Badal.
iv) The last performance was by Rani; this item was assigned by Gagan.
v) The items assigned by Ashman were performed consecutively. The number of performances between items assigned by each of the remaining composers was the same.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
The figure below shows the street map for a certain region with the street intersections marked from a through l. A person standing at an intersection can see along straight lines to other intersections that are in her line of sight and all other people standing at these intersections. For example, a person standing at intersection g can see all people standing at intersections b, c, e, f, h, and k. In particular, the person standing at intersection g can see the person standing at intersection e irrespective of whether there is a person standing at
intersection f.
Six people U, V, W, X, Y, and Z, are standing at different intersections. No two people are standing at the same intersection.
The following additional facts are known.
1. X, U, and Z are standing at the three corners of a triangle formed by three street segments.
2. X can see only U and Z.
3. Y can see only U and W.
4. U sees V standing in the next intersection behind Z.
5. W cannot see V or Z.
6. No one among the six is standing at intersection d.
CAT/2019.1(DILR)
Question. 85
Six people U, V, W, X, Y, and Z, are standing at different intersections. No two people are standing at the same intersection.
The following additional facts are known.
1. X, U, and Z are standing at the three corners of a triangle formed by three street segments.
2. X can see only U and Z.
3. Y can see only U and W.
4. U sees V standing in the next intersection behind Z.
5. W cannot see V or Z.
6. No one among the six is standing at intersection d.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
The figure below shows the street map for a certain region with the street intersections marked from a through l. A person standing at an intersection can see along straight lines to other intersections that are in her line of sight and all other people standing at these intersections. For example, a person standing at intersection g can see all people standing at intersections b, c, e, f, h, and k. In particular, the person standing at intersection g can see the person standing at intersection e irrespective of whether there is a person standing at
intersection f.

Six people U, V, W, X, Y, and Z, are standing at different intersections. No two people are standing at the same intersection.
The following additional facts are known.
1. X, U, and Z are standing at the three corners of a triangle formed by three street segments.
2. X can see only U and Z.
3. Y can see only U and W.
4. U sees V standing in the next intersection behind Z.
5. W cannot see V or Z.
6. No one among the six is standing at intersection d.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
The figure below shows the street map for a certain region with the street intersections marked from a through l. A person standing at an intersection can see along straight lines to other intersections that are in her line of sight and all other people standing at these intersections. For example, a person standing at intersection g can see all people standing at intersections b, c, e, f, h, and k. In particular, the person standing at intersection g can see the person standing at intersection e irrespective of whether there is a person standing at
intersection f.

Six people U, V, W, X, Y, and Z, are standing at different intersections. No two people are standing at the same intersection.
The following additional facts are known.
1. X, U, and Z are standing at the three corners of a triangle formed by three street segments.
2. X can see only U and Z.
3. Y can see only U and W.
4. U sees V standing in the next intersection behind Z.
5. W cannot see V or Z.
6. No one among the six is standing at intersection d.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
The figure below shows the street map for a certain region with the street intersections marked from a through l. A person standing at an intersection can see along straight lines to other intersections that are in her line of sight and all other people standing at these intersections. For example, a person standing at intersection g can see all people standing at intersections b, c, e, f, h, and k. In particular, the person standing at intersection g can see the person standing at intersection e irrespective of whether there is a person standing at
intersection f.

Six people U, V, W, X, Y, and Z, are standing at different intersections. No two people are standing at the same intersection.
The following additional facts are known.
1. X, U, and Z are standing at the three corners of a triangle formed by three street segments.
2. X can see only U and Z.
3. Y can see only U and W.
4. U sees V standing in the next intersection behind Z.
5. W cannot see V or Z.
6. No one among the six is standing at intersection d.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
A new game show on TV has 100 boxes numbered 1, 2, ....., 100 in a row, each containing a mystery prize. The prizes are items of different types, a, b, c, ....., in decreasing order of value. The most expensive item is of type a, a diamond ring, and there is exactly one of these. You are told that the number of items at least doubles as you move to the next type. For example, there would be at least twice as many items of type b as of type a, at least twice as many items of type c as of type b and so on. There is no particular order in which the prizes are placed in the boxes.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
A new game show on TV has 100 boxes numbered 1, 2, ....., 100 in a row, each containing a mystery prize. The prizes are items of different types, a, b, c, ....., in decreasing order of value. The most expensive item is of type a, a diamond ring, and there is exactly one of these. You are told that the number of items at least doubles as you move to the next type. For example, there would be at least twice as many items of type b as of type a, at least twice as many items of type c as of type b and so on. There is no particular order in which the prizes are placed in the boxes.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
A new game show on TV has 100 boxes numbered 1, 2, ....., 100 in a row, each containing a mystery prize. The prizes are items of different types, a, b, c, ....., in decreasing order of value. The most expensive item is of type a, a diamond ring, and there is exactly one of these. You are told that the number of items at least doubles as you move to the next type. For example, there would be at least twice as many items of type b as of type a, at least twice as many items of type c as of type b and so on. There is no particular order in which the prizes are placed in the boxes.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
A new game show on TV has 100 boxes numbered 1, 2, ....., 100 in a row, each containing a mystery prize. The prizes are items of different types, a, b, c, ....., in decreasing order of value. The most expensive item is of type a, a diamond ring, and there is exactly one of these. You are told that the number of items at least doubles as you move to the next type. For example, there would be at least twice as many items of type b as of type a, at least twice as many items of type c as of type b and so on. There is no particular order in which the prizes are placed in the boxes.
CAT/2019.1(DILR)
Question. 92
You ask for the type of item in box 45. Instead of being given a direct answer, you are told that there are 31 items of the same type as box 45 in boxes 1 to 44 and 43 items of the same type as box 45 in boxes 46 to 100. What is the maximum possible number of different types of items?
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
The first year students in a business school are split into six sections. In 2019 the Business Statistics course was taught in these six sections by Annie, Beti, Chetan, Dave, Esha, and Fakir. All six sections had a common midterm (MT) and a common endterm (ET) worth 100 marks each. ET contained more questions than MT. Questions for MT and ET were prepared collectively by the six faculty members. Considering MT and ET together, each faculty member prepared the same number of questions. Each of MT and ET had at least four questions that were worth 5 marks, at least three questions that were worth 10 marks, and at least two questions that were worth 15 marks. In both MT and ET, all the 5-mark questions preceded the 10-mark questions, and all the 15-mark questions followed the 10-mark questions.
The following additional facts are known.
i. Annie prepared the fifth question for both MT and ET. For MT, this question carried 5 marks.
ii. Annie prepared one question for MT. Every other faculty member prepared more than one questions for MT.
iii. All questions prepared by a faculty member appeared consecutively in MT as well as ET.
iv. Chetan prepared the third question in both MT and ET; and Esha prepared the eighth question in both.
v. Fakir prepared the first question of MT and the last one in ET. Dave prepared the last question of MT and the first one in ET.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
The first year students in a business school are split into six sections. In 2019 the Business Statistics course was taught in these six sections by Annie, Beti, Chetan, Dave, Esha, and Fakir. All six sections had a common midterm (MT) and a common endterm (ET) worth 100 marks each. ET contained more questions than MT. Questions for MT and ET were prepared collectively by the six faculty members. Considering MT and ET together, each faculty member prepared the same number of questions. Each of MT and ET had at least four questions that were worth 5 marks, at least three questions that were worth 10 marks, and at least two questions that were worth 15 marks. In both MT and ET, all the 5-mark questions preceded the 10-mark questions, and all the 15-mark questions followed the 10-mark questions.
The following additional facts are known.
i. Annie prepared the fifth question for both MT and ET. For MT, this question carried 5 marks.
ii. Annie prepared one question for MT. Every other faculty member prepared more than one questions for MT.
iii. All questions prepared by a faculty member appeared consecutively in MT as well as ET.
iv. Chetan prepared the third question in both MT and ET; and Esha prepared the eighth question in both.
v. Fakir prepared the first question of MT and the last one in ET. Dave prepared the last question of MT and the first one in ET.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
The first year students in a business school are split into six sections. In 2019 the Business Statistics course was taught in these six sections by Annie, Beti, Chetan, Dave, Esha, and Fakir. All six sections had a common midterm (MT) and a common endterm (ET) worth 100 marks each. ET contained more questions than MT. Questions for MT and ET were prepared collectively by the six faculty members. Considering MT and ET together, each faculty member prepared the same number of questions. Each of MT and ET had at least four questions that were worth 5 marks, at least three questions that were worth 10 marks, and at least two questions that were worth 15 marks. In both MT and ET, all the 5-mark questions preceded the 10-mark questions, and all the 15-mark questions followed the 10-mark questions.
The following additional facts are known.
i. Annie prepared the fifth question for both MT and ET. For MT, this question carried 5 marks.
ii. Annie prepared one question for MT. Every other faculty member prepared more than one questions for MT.
iii. All questions prepared by a faculty member appeared consecutively in MT as well as ET.
iv. Chetan prepared the third question in both MT and ET; and Esha prepared the eighth question in both.
v. Fakir prepared the first question of MT and the last one in ET. Dave prepared the last question of MT and the first one in ET.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
The first year students in a business school are split into six sections. In 2019 the Business Statistics course was taught in these six sections by Annie, Beti, Chetan, Dave, Esha, and Fakir. All six sections had a common midterm (MT) and a common endterm (ET) worth 100 marks each. ET contained more questions than MT. Questions for MT and ET were prepared collectively by the six faculty members. Considering MT and ET together, each faculty member prepared the same number of questions. Each of MT and ET had at least four questions that were worth 5 marks, at least three questions that were worth 10 marks, and at least two questions that were worth 15 marks. In both MT and ET, all the 5-mark questions preceded the 10-mark questions, and all the 15-mark questions followed the 10-mark questions.
The following additional facts are known.
i. Annie prepared the fifth question for both MT and ET. For MT, this question carried 5 marks.
ii. Annie prepared one question for MT. Every other faculty member prepared more than one questions for MT.
iii. All questions prepared by a faculty member appeared consecutively in MT as well as ET.
iv. Chetan prepared the third question in both MT and ET; and Esha prepared the eighth question in both.
v. Fakir prepared the first question of MT and the last one in ET. Dave prepared the last question of MT and the first one in ET.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
In the table below the check marks indicate all languages spoken by five people: Paula, Quentin, Robert, Sally, and Terence. For example, Paula speaks only Chinese and English.
These five people form three teams, Team 1, Team 2 and Team 3. Each team has either 2 or 3 members. A team is said to speak a
particular language if at least one of its members speak that language.
The following facts are known.
(1) Each team speaks exactly four languages and has the same number of members.
(2) English and Chinese are spoken by all three teams, Basque and French by exactly two teams and the other languages by exactly one team.
(3) None of the teams include both Quentin and Robert.
(4) Paula and Sally are together in exactly two teams.
(5) Robert is in Team 1 and Quentin is in Team 3.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
In the table below the check marks indicate all languages spoken by five people: Paula, Quentin, Robert, Sally, and Terence. For example, Paula speaks only Chinese and English.
These five people form three teams, Team 1, Team 2 and Team 3. Each team has either 2 or 3 members. A team is said to speak a
particular language if at least one of its members speak that language.
The following facts are known.
(1) Each team speaks exactly four languages and has the same number of members.
(2) English and Chinese are spoken by all three teams, Basque and French by exactly two teams and the other languages by exactly one team.
(3) None of the teams include both Quentin and Robert.
(4) Paula and Sally are together in exactly two teams.
(5) Robert is in Team 1 and Quentin is in Team 3.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
In the table below the check marks indicate all languages spoken by five people: Paula, Quentin, Robert, Sally, and Terence. For example, Paula speaks only Chinese and English.
These five people form three teams, Team 1, Team 2 and Team 3. Each team has either 2 or 3 members. A team is said to speak a
particular language if at least one of its members speak that language.
The following facts are known.
(1) Each team speaks exactly four languages and has the same number of members.
(2) English and Chinese are spoken by all three teams, Basque and French by exactly two teams and the other languages by exactly one team.
(3) None of the teams include both Quentin and Robert.
(4) Paula and Sally are together in exactly two teams.
(5) Robert is in Team 1 and Quentin is in Team 3.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
In the table below the check marks indicate all languages spoken by five people: Paula, Quentin, Robert, Sally, and Terence. For example, Paula speaks only Chinese and English.
These five people form three teams, Team 1, Team 2 and Team 3. Each team has either 2 or 3 members. A team is said to speak a
particular language if at least one of its members speak that language.
The following facts are known.
(1) Each team speaks exactly four languages and has the same number of members.
(2) English and Chinese are spoken by all three teams, Basque and French by exactly two teams and the other languages by exactly one team.
(3) None of the teams include both Quentin and Robert.
(4) Paula and Sally are together in exactly two teams.
(5) Robert is in Team 1 and Quentin is in Team 3.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Students in a college are discussing two proposals --
A: a proposal by the authorities to introduce dress code on campus, and
B: a proposal by the students to allow multinational food franchises to set up outlets on college campus.
A student does not necessarily support either of the two proposals. In an upcoming election for student union president, there are two candidates in fray: Sunita and Ragini. Every student prefers one of the two candidates. A survey was conducted among the students by picking a sample of 500 students.
The following information was noted from this survey.
1. 250 students supported proposal A and 250 students supported proposal B.
2. Among the 200 students who preferred Sunita as student union president, 80% supported proposal A.
3. Among those who preferred Ragini, 30% supported proposal A.
4. 20% of those who supported proposal B preferred Sunita.
5. 40% of those who did not support proposal B preferred Ragini.
6. Every student who preferred Sunita and supported proposal B also supported proposal A.
7. Among those who preferred Ragini, 20% did not support any of the proposals.
CAT/2019.2(DILR)
Question. 101
Among the students surveyed who supported proposal A, what percentage preferred Sunita for student union president?
64
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Students in a college are discussing two proposals --
A: a proposal by the authorities to introduce dress code on campus, and
B: a proposal by the students to allow multinational food franchises to set up outlets on college campus.
A student does not necessarily support either of the two proposals. In an upcoming election for student union president, there are two candidates in fray: Sunita and Ragini. Every student prefers one of the two candidates. A survey was conducted among the students by picking a sample of 500 students.
The following information was noted from this survey.
1. 250 students supported proposal A and 250 students supported proposal B.
2. Among the 200 students who preferred Sunita as student union president, 80% supported proposal A.
3. Among those who preferred Ragini, 30% supported proposal A.
4. 20% of those who supported proposal B preferred Sunita.
5. 40% of those who did not support proposal B preferred Ragini.
6. Every student who preferred Sunita and supported proposal B also supported proposal A.
7. Among those who preferred Ragini, 20% did not support any of the proposals.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Students in a college are discussing two proposals --
A: a proposal by the authorities to introduce dress code on campus, and
B: a proposal by the students to allow multinational food franchises to set up outlets on college campus.
A student does not necessarily support either of the two proposals. In an upcoming election for student union president, there are two candidates in fray: Sunita and Ragini. Every student prefers one of the two candidates. A survey was conducted among the students by picking a sample of 500 students.
The following information was noted from this survey.
1. 250 students supported proposal A and 250 students supported proposal B.
2. Among the 200 students who preferred Sunita as student union president, 80% supported proposal A.
3. Among those who preferred Ragini, 30% supported proposal A.
4. 20% of those who supported proposal B preferred Sunita.
5. 40% of those who did not support proposal B preferred Ragini.
6. Every student who preferred Sunita and supported proposal B also supported proposal A.
7. Among those who preferred Ragini, 20% did not support any of the proposals.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Students in a college are discussing two proposals --
A: a proposal by the authorities to introduce dress code on campus, and
B: a proposal by the students to allow multinational food franchises to set up outlets on college campus.
A student does not necessarily support either of the two proposals. In an upcoming election for student union president, there are two candidates in fray: Sunita and Ragini. Every student prefers one of the two candidates. A survey was conducted among the students by picking a sample of 500 students.
The following information was noted from this survey.
1. 250 students supported proposal A and 250 students supported proposal B.
2. Among the 200 students who preferred Sunita as student union president, 80% supported proposal A.
3. Among those who preferred Ragini, 30% supported proposal A.
4. 20% of those who supported proposal B preferred Sunita.
5. 40% of those who did not support proposal B preferred Ragini.
6. Every student who preferred Sunita and supported proposal B also supported proposal A.
7. Among those who preferred Ragini, 20% did not support any of the proposals.
CAT/2019.2(DILR)
Question. 104
What percentage of the students surveyed who did not support proposal A preferred Ragini as student union president?
84
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Fuel contamination levels at each of 20 petrol pumps P1, P2, …, P20 were recorded as either high, medium, or low.
1. Contamination levels at three pumps among P1 – P5 were recorded as high.
2. P6 was the only pump among P1 – P10 where the contamination level was recorded as low.
3. P7 and P8 were the only two consecutively numbered pumps where the same levels of contamination were recorded.
4. High contamination levels were not recorded at any of the pumps P16 – P20.
5. The number of pumps where high contamination levels were recorded was twice the number of pumps where low contamination levels were recorded.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Fuel contamination levels at each of 20 petrol pumps P1, P2, …, P20 were recorded as either high, medium, or low.
1. Contamination levels at three pumps among P1 – P5 were recorded as high.
2. P6 was the only pump among P1 – P10 where the contamination level was recorded as low.
3. P7 and P8 were the only two consecutively numbered pumps where the same levels of contamination were recorded.
4. High contamination levels were not recorded at any of the pumps P16 – P20.
5. The number of pumps where high contamination levels were recorded was twice the number of pumps where low contamination levels were recorded.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Fuel contamination levels at each of 20 petrol pumps P1, P2, …, P20 were recorded as either high, medium, or low.
1. Contamination levels at three pumps among P1 – P5 were recorded as high.
2. P6 was the only pump among P1 – P10 where the contamination level was recorded as low.
3. P7 and P8 were the only two consecutively numbered pumps where the same levels of contamination were recorded.
4. High contamination levels were not recorded at any of the pumps P16 – P20.
5. The number of pumps where high contamination levels were recorded was twice the number of pumps where low contamination levels were recorded.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Fuel contamination levels at each of 20 petrol pumps P1, P2, …, P20 were recorded as either high, medium, or low.
1. Contamination levels at three pumps among P1 – P5 were recorded as high.
2. P6 was the only pump among P1 – P10 where the contamination level was recorded as low.
3. P7 and P8 were the only two consecutively numbered pumps where the same levels of contamination were recorded.
4. High contamination levels were not recorded at any of the pumps P16 – P20.
5. The number of pumps where high contamination levels were recorded was twice the number of pumps where low contamination levels were recorded.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Adriana, Bandita, Chitra, and Daisy are four female students, and Amit, Barun, Chetan, and Deb are four male students. Each of them studies in one of three institutes - X, Y, and Z. Each student majors in one subject among Marketing, Operations, and Finance, and minors in a different one among these three subjects. The following facts are known about the eight students:
1. Three students are from X, three are from Y, and the remaining two students, both female, are from Z.
2. Both the male students from Y minor in Finance, while the female student from Y majors in Operations.
3. Only one male student majors in Operations, while three female students minor in Marketing.
4. One female and two male students major in Finance.
5. Adriana and Deb are from the same institute. Daisy and Amit are from the same institute.
6. Barun is from Y and majors in Operations. Chetan is from X and majors in Finance.
7. Daisy minors in Operations.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Adriana, Bandita, Chitra, and Daisy are four female students, and Amit, Barun, Chetan, and Deb are four male students. Each of them studies in one of three institutes - X, Y, and Z. Each student majors in one subject among Marketing, Operations, and Finance, and minors in a different one among these three subjects. The following facts are known about the eight students:
1. Three students are from X, three are from Y, and the remaining two students, both female, are from Z.
2. Both the male students from Y minor in Finance, while the female student from Y majors in Operations.
3. Only one male student majors in Operations, while three female students minor in Marketing.
4. One female and two male students major in Finance.
5. Adriana and Deb are from the same institute. Daisy and Amit are from the same institute.
6. Barun is from Y and majors in Operations. Chetan is from X and majors in Finance.
7. Daisy minors in Operations.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Adriana, Bandita, Chitra, and Daisy are four female students, and Amit, Barun, Chetan, and Deb are four male students. Each of them studies in one of three institutes - X, Y, and Z. Each student majors in one subject among Marketing, Operations, and Finance, and minors in a different one among these three subjects. The following facts are known about the eight students:
1. Three students are from X, three are from Y, and the remaining two students, both female, are from Z.
2. Both the male students from Y minor in Finance, while the female student from Y majors in Operations.
3. Only one male student majors in Operations, while three female students minor in Marketing.
4. One female and two male students major in Finance.
5. Adriana and Deb are from the same institute. Daisy and Amit are from the same institute.
6. Barun is from Y and majors in Operations. Chetan is from X and majors in Finance.
7. Daisy minors in Operations.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Adriana, Bandita, Chitra, and Daisy are four female students, and Amit, Barun, Chetan, and Deb are four male students. Each of them studies in one of three institutes - X, Y, and Z. Each student majors in one subject among Marketing, Operations, and Finance, and minors in a different one among these three subjects. The following facts are known about the eight students:
1. Three students are from X, three are from Y, and the remaining two students, both female, are from Z.
2. Both the male students from Y minor in Finance, while the female student from Y majors in Operations.
3. Only one male student majors in Operations, while three female students minor in Marketing.
4. One female and two male students major in Finance.
5. Adriana and Deb are from the same institute. Daisy and Amit are from the same institute.
6. Barun is from Y and majors in Operations. Chetan is from X and majors in Finance.
7. Daisy minors in Operations.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Twenty four people are part of three committees which are to look at research, teaching, and administration respectively. No two committees have any member in common. No two committees are of the same size. Each committee has three types of people: bureaucrats, educationalists, and politicians, with at least one from each of the three types in each committee. The following facts are also known about the committees:
1. The numbers of bureaucrats in the research and teaching committees are equal, while the number of bureaucrats in the research committee is 75% of the number of bureaucrats in the administration committee.
2. The number of educationalists in the teaching committee is less than the number of educationalists in the research committee. The number of educationalists in the research committee is the average of the numbers of educationalists in the other two committees.
3. 60% of the politicians are in the administration committee, and 20% are in the teaching committee.
CAT/2018.1(DILR)
Question. 113
Based on the given information, which of the following statements MUST be FALSE?
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Twenty four people are part of three committees which are to look at research, teaching, and administration respectively. No two committees have any member in common. No two committees are of the same size. Each committee has three types of people: bureaucrats, educationalists, and politicians, with at least one from each of the three types in each committee. The following facts are also known about the committees:
1. The numbers of bureaucrats in the research and teaching committees are equal, while the number of bureaucrats in the research committee is 75% of the number of bureaucrats in the administration committee.
2. The number of educationalists in the teaching committee is less than the number of educationalists in the research committee. The number of educationalists in the research committee is the average of the numbers of educationalists in the other two committees.
3. 60% of the politicians are in the administration committee, and 20% are in the teaching committee.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Twenty four people are part of three committees which are to look at research, teaching, and administration respectively. No two committees have any member in common. No two committees are of the same size. Each committee has three types of people: bureaucrats, educationalists, and politicians, with at least one from each of the three types in each committee. The following facts are also known about the committees:
1. The numbers of bureaucrats in the research and teaching committees are equal, while the number of bureaucrats in the research committee is 75% of the number of bureaucrats in the administration committee.
2. The number of educationalists in the teaching committee is less than the number of educationalists in the research committee. The number of educationalists in the research committee is the average of the numbers of educationalists in the other two committees.
3. 60% of the politicians are in the administration committee, and 20% are in the teaching committee.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Twenty four people are part of three committees which are to look at research, teaching, and administration respectively. No two committees have any member in common. No two committees are of the same size. Each committee has three types of people: bureaucrats, educationalists, and politicians, with at least one from each of the three types in each committee. The following facts are also known about the committees:
1. The numbers of bureaucrats in the research and teaching committees are equal, while the number of bureaucrats in the research committee is 75% of the number of bureaucrats in the administration committee.
2. The number of educationalists in the teaching committee is less than the number of educationalists in the research committee. The number of educationalists in the research committee is the average of the numbers of educationalists in the other two committees.
3. 60% of the politicians are in the administration committee, and 20% are in the teaching committee.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Fun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:
1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.
2. There are a total of 17 students enrolled in G.
3. The number of students enrolled only in G is one less than the number of students enrolled only in L.
4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.
5. The maximum student enrollment is in L.
6. Ten students enrolled in G are also enrolled in at least one more sport.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Fun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:
1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.
2. There are a total of 17 students enrolled in G.
3. The number of students enrolled only in G is one less than the number of students enrolled only in L.
4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.
5. The maximum student enrollment is in L.
6. Ten students enrolled in G are also enrolled in at least one more sport.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Fun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:
1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.
2. There are a total of 17 students enrolled in G.
3. The number of students enrolled only in G is one less than the number of students enrolled only in L.
4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.
5. The maximum student enrollment is in L.
6. Ten students enrolled in G are also enrolled in at least one more sport.
CAT/2018.2(DILR)
Question. 119
Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one.After the withdrawal, how many students were enrolled in both G and K?
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Fun Sports (FS) provides training in three sports - Gilli-danda (G), Kho-Kho (K), and Ludo (L). Currently it has an enrollment of 39 students each of whom is enrolled in at least one of the three sports. The following details are known:
1. The number of students enrolled only in L is double the number of students enrolled in all the three sports.
2. There are a total of 17 students enrolled in G.
3. The number of students enrolled only in G is one less than the number of students enrolled only in L.
4. The number of students enrolled only in K is equal to the number of students who are enrolled in both K and L.
5. The maximum student enrollment is in L.
6. Ten students enrolled in G are also enrolled in at least one more sport.
CAT/2018.2(DILR)
Question. 120
Due to academic pressure, students who were enrolled in all three sports were asked to withdraw from one of the three sports. After the withdrawal, the number of students enrolled in G was six less than the number of students enrolled in L, while the number of students enrolled in K went down by one.After the withdrawal, how many students were enrolled in both G and L?
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Each visitor to an amusement park needs to buy a ticket. Tickets can be Platinum, Gold, or Economy. Visitors are classified as Old, Middle-aged, or Young. The following facts are known about visitors and ticket sales on a particular day:
1. 140 tickets were sold.
2. The number of Middle-aged visitors was twice the number of Old visitors, while the number of Young visitors was twice the number of Middle-aged visitors.
3. Young visitors bought 38 of the 55 Economy tickets that were sold, and they bought half the total number of Platinum tickets that were sold.
4. The number of Gold tickets bought by Old visitors was equal to the number of Economy tickets bought by Old visitors.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Each visitor to an amusement park needs to buy a ticket. Tickets can be Platinum, Gold, or Economy. Visitors are classified as Old, Middle-aged, or Young. The following facts are known about visitors and ticket sales on a particular day:
1. 140 tickets were sold.
2. The number of Middle-aged visitors was twice the number of Old visitors, while the number of Young visitors was twice the number of Middle-aged visitors.
3. Young visitors bought 38 of the 55 Economy tickets that were sold, and they bought half the total number of Platinum tickets that were sold.
4. The number of Gold tickets bought by Old visitors was equal to the number of Economy tickets bought by Old visitors.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Each visitor to an amusement park needs to buy a ticket. Tickets can be Platinum, Gold, or Economy. Visitors are classified as Old, Middle-aged, or Young. The following facts are known about visitors and ticket sales on a particular day:
1. 140 tickets were sold.
2. The number of Middle-aged visitors was twice the number of Old visitors, while the number of Young visitors was twice the number of Middle-aged visitors.
3. Young visitors bought 38 of the 55 Economy tickets that were sold, and they bought half the total number of Platinum tickets that were sold.
4. The number of Gold tickets bought by Old visitors was equal to the number of Economy tickets bought by Old visitors.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
Each visitor to an amusement park needs to buy a ticket. Tickets can be Platinum, Gold, or Economy. Visitors are classified as Old, Middle-aged, or Young. The following facts are known about visitors and ticket sales on a particular day:
1. 140 tickets were sold.
2. The number of Middle-aged visitors was twice the number of Old visitors, while the number of Young visitors was twice the number of Middle-aged visitors.
3. Young visitors bought 38 of the 55 Economy tickets that were sold, and they bought half the total number of Platinum tickets that were sold.
4. The number of Gold tickets bought by Old visitors was equal to the number of Economy tickets bought by Old visitors.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
According to a coding scheme the sentence,
Peacock is designated as the national bird of India is coded as 5688999 35 1135556678 56 458 13666689 1334 79 13366
This coding scheme has the following rules:
1. The scheme is case-insensitive (does not distinguish between upper case and lower case letters).
2. Each letter has a unique code which is a single digit from among 1,2,3,......,9.
3. The digit 9 codes two letters, and every other digit codes three letters.
4. The code for a word is constructed by arranging the digits corresponding to its letters in a non-decreasing sequence.
Answer these questions on the basis of this information
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
According to a coding scheme the sentence,
Peacock is designated as the national bird of India is coded as 5688999 35 1135556678 56 458 13666689 1334 79 13366
This coding scheme has the following rules:
1. The scheme is case-insensitive (does not distinguish between upper case and lower case letters).
2. Each letter has a unique code which is a single digit from among 1,2,3,......,9.
3. The digit 9 codes two letters, and every other digit codes three letters.
4. The code for a word is constructed by arranging the digits corresponding to its letters in a non-decreasing sequence.
Answer these questions on the basis of this information
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
According to a coding scheme the sentence,
Peacock is designated as the national bird of India is coded as 5688999 35 1135556678 56 458 13666689 1334 79 13366
This coding scheme has the following rules:
1. The scheme is case-insensitive (does not distinguish between upper case and lower case letters).
2. Each letter has a unique code which is a single digit from among 1,2,3,......,9.
3. The digit 9 codes two letters, and every other digit codes three letters.
4. The code for a word is constructed by arranging the digits corresponding to its letters in a non-decreasing sequence.
Answer these questions on the basis of this information
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
According to a coding scheme the sentence,
Peacock is designated as the national bird of India is coded as 5688999 35 1135556678 56 458 13666689 1334 79 13366
This coding scheme has the following rules:
1. The scheme is case-insensitive (does not distinguish between upper case and lower case letters).
2. Each letter has a unique code which is a single digit from among 1,2,3,......,9.
3. The digit 9 codes two letters, and every other digit codes three letters.
4. The code for a word is constructed by arranging the digits corresponding to its letters in a non-decreasing sequence.
Answer these questions on the basis of this information
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
There are 21 employees working in a division, out of whom 10 are special-skilled employees (SE) and the remaining are regular skilled employees (RE). During the next five months, the division has to complete five projects every month. Out of the 25 projects, 5 projects are "challenging", while the remaining ones are "standard". Each of the challenging projects has to be completed in different months. Every month, five teams - T1, T2, T3, T4 and T5, work on one project each. T1, T2, T3, T4 and T5 are allotted the challenging project in the first, second, third, fourth and fifth month, respectively. The team assigned the challenging project has one more employee than the rest.
In the first month, T1 has one more SE than T2, T2 has one more SE than T3, T3 has one more SE than T4, and T4 has one more SE than T5. Between two successive months, the composition of the teams changes as follows:
a. The team allotted the challenging project, gets two SE from the team which was allotted the challenging project in the previous month. In exchange, one RE is shifted from the former team to the latter team.
b. After the above exchange, if T1 has any SE and T5 has any RE, then one SE is shifted from T1 to T5, and one RE is shifted from T 5 to T1. Also, if T2 has any SE and T4 has any RE, then one SE is shifted from T2 to T4, and one RE is shifted from T4 to T2.
Each standard project has a total of 100 credit points, while each challenging project has 200 credit points. The credit points are equally shared between the employees included in that team.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
There are 21 employees working in a division, out of whom 10 are special-skilled employees (SE) and the remaining are regular skilled employees (RE). During the next five months, the division has to complete five projects every month. Out of the 25 projects, 5 projects are "challenging", while the remaining ones are "standard". Each of the challenging projects has to be completed in different months. Every month, five teams - T1, T2, T3, T4 and T5, work on one project each. T1, T2, T3, T4 and T5 are allotted the challenging project in the first, second, third, fourth and fifth month, respectively. The team assigned the challenging project has one more employee than the rest.
In the first month, T1 has one more SE than T2, T2 has one more SE than T3, T3 has one more SE than T4, and T4 has one more SE than T5. Between two successive months, the composition of the teams changes as follows:
a. The team allotted the challenging project, gets two SE from the team which was allotted the challenging project in the previous month. In exchange, one RE is shifted from the former team to the latter team.
b. After the above exchange, if T1 has any SE and T5 has any RE, then one SE is shifted from T1 to T5, and one RE is shifted from T 5 to T1. Also, if T2 has any SE and T4 has any RE, then one SE is shifted from T2 to T4, and one RE is shifted from T4 to T2.
Each standard project has a total of 100 credit points, while each challenging project has 200 credit points. The credit points are equally shared between the employees included in that team.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
There are 21 employees working in a division, out of whom 10 are special-skilled employees (SE) and the remaining are regular skilled employees (RE). During the next five months, the division has to complete five projects every month. Out of the 25 projects, 5 projects are "challenging", while the remaining ones are "standard". Each of the challenging projects has to be completed in different months. Every month, five teams - T1, T2, T3, T4 and T5, work on one project each. T1, T2, T3, T4 and T5 are allotted the challenging project in the first, second, third, fourth and fifth month, respectively. The team assigned the challenging project has one more employee than the rest.
In the first month, T1 has one more SE than T2, T2 has one more SE than T3, T3 has one more SE than T4, and T4 has one more SE than T5. Between two successive months, the composition of the teams changes as follows:
a. The team allotted the challenging project, gets two SE from the team which was allotted the challenging project in the previous month. In exchange, one RE is shifted from the former team to the latter team.
b. After the above exchange, if T1 has any SE and T5 has any RE, then one SE is shifted from T1 to T5, and one RE is shifted from T 5 to T1. Also, if T2 has any SE and T4 has any RE, then one SE is shifted from T2 to T4, and one RE is shifted from T4 to T2.
Each standard project has a total of 100 credit points, while each challenging project has 200 credit points. The credit points are equally shared between the employees included in that team.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
There are 21 employees working in a division, out of whom 10 are special-skilled employees (SE) and the remaining are regular skilled employees (RE). During the next five months, the division has to complete five projects every month. Out of the 25 projects, 5 projects are "challenging", while the remaining ones are "standard". Each of the challenging projects has to be completed in different months. Every month, five teams - T1, T2, T3, T4 and T5, work on one project each. T1, T2, T3, T4 and T5 are allotted the challenging project in the first, second, third, fourth and fifth month, respectively. The team assigned the challenging project has one more employee than the rest.
In the first month, T1 has one more SE than T2, T2 has one more SE than T3, T3 has one more SE than T4, and T4 has one more SE than T5. Between two successive months, the composition of the teams changes as follows:
a. The team allotted the challenging project, gets two SE from the team which was allotted the challenging project in the previous month. In exchange, one RE is shifted from the former team to the latter team.
b. After the above exchange, if T1 has any SE and T5 has any RE, then one SE is shifted from T1 to T5, and one RE is shifted from T 5 to T1. Also, if T2 has any SE and T4 has any RE, then one SE is shifted from T2 to T4, and one RE is shifted from T4 to T2.
Each standard project has a total of 100 credit points, while each challenging project has 200 credit points. The credit points are equally shared between the employees included in that team.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
A high security research lab requires the researchers to set a pass key sequence based on the scan of the five fingers of their left hands. When an employee first joins the lab, her fingers are scanned in an order of her choice, and then when she wants to re-enter the facility, she has to scan the five fingers in the same sequence.
The lab authorities are considering some relaxations of the scan order requirements, since it is observed that some employees often get locked-out because they forget the sequence.
The lab has decided to allow a variation in the sequence of scans of the five fingers so that at most two scans (out of five) are out of place. For example, if the original sequence is Thumb (T), index finger (I), middle finger (M), ring finger (R) and little finger (L) then TLMRI is also allowed, but TMRLI is not.
CAT/2017.2(DILR)
Question. 133
The lab has decided to allow a variation in the sequence of scans of the five fingers so that at most two scans (out of five) are out of place. For example, if the original sequence is Thumb (T), index finger (I), middle finger (M), ring finger (R) and little finger (L) then TLMRI is also allowed, but TMRLI is not. How many different sequences of scans are allowed for any given person's original scan?
11
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
A high security research lab requires the researchers to set a pass key sequence based on the scan of the five fingers of their left hands. When an employee first joins the lab, her fingers are scanned in an order of her choice, and then when she wants to re-enter the facility, she has to scan the five fingers in the same sequence.
The lab authorities are considering some relaxations of the scan order requirements, since it is observed that some employees often get locked-out because they forget the sequence.
The lab has decided to allow a variation in the sequence of scans of the five fingers so that at most two scans (out of five) are out of place. For example, if the original sequence is Thumb (T), index finger (I), middle finger (M), ring finger (R) and little finger (L) then TLMRI is also allowed, but TMRLI is not.
CAT/2017.2(DILR)
Question. 134
The lab has decided to allow variations of the original sequence so that input of the scanned sequence of five fingers is allowed to vary from the original sequence by one place for any of the fingers. Thus, for example, if TIMRL is the original sequence, then ITRML is allowed, but LIMRT is not. How many different sequences are allowed for any given person's original scan?
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
A high security research lab requires the researchers to set a pass key sequence based on the scan of the five fingers of their left hands. When an employee first joins the lab, her fingers are scanned in an order of her choice, and then when she wants to re-enter the facility, she has to scan the five fingers in the same sequence.
The lab authorities are considering some relaxations of the scan order requirements, since it is observed that some employees often get locked-out because they forget the sequence.
The lab has decided to allow a variation in the sequence of scans of the five fingers so that at most two scans (out of five) are out of place. For example, if the original sequence is Thumb (T), index finger (I), middle finger (M), ring finger (R) and little finger (L) then TLMRI is also allowed, but TMRLI is not.
CAT/2017.2(DILR)
Question. 135
The lab has now decided to require six scans in the pass sequence, where exactly one finger is scanned twice, and the other fingers are scanned once, which can be done in any order. For example a possible sequence is TIMTRL.
Suppose the lab allows a variation of the original sequence (of six inputs) where at most two scans are out of place, as long as the finger originally scanned twice is scanned twice and other fingers are scanned once. How many different sequences of scans are allowed for any given person's original scan?
15
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
A high security research lab requires the researchers to set a pass key sequence based on the scan of the five fingers of their left hands. When an employee first joins the lab, her fingers are scanned in an order of her choice, and then when she wants to re-enter the facility, she has to scan the five fingers in the same sequence.
The lab authorities are considering some relaxations of the scan order requirements, since it is observed that some employees often get locked-out because they forget the sequence.
The lab has decided to allow a variation in the sequence of scans of the five fingers so that at most two scans (out of five) are out of place. For example, if the original sequence is Thumb (T), index finger (I), middle finger (M), ring finger (R) and little finger (L) then TLMRI is also allowed, but TMRLI is not.
CAT/2017.2(DILR)
Question. 136
The lab has now decided to require six scans in the pass sequence, where exactly one finger is scanned twice, and the other fingers are scanned once, which can be done in any order. For example a possible sequence is TIMTRL.
Suppose the lab allows a variation of the original sequence (of six inputs) so that input in the form of scanned sequence of six fingers is allowed to vary from the original sequence by one place for any of the fingers, as long as the finger originally scanned twice is scanned twice and other fingers are scanned once. How many different sequences of scans are allowed if the original sequence is LRLTIM?
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
A tea taster was assigned to rate teas from six different locations - Munnar, Wayanad, Ooty, Darjeeling, Assam and Himachal. These teas were placed in six cups, numbered 1 to 6, not necessarily in the same order. The tea taster was asked to rate these teas on the strength of their flavour on a scale of 1 to 10. He gave a unique integer rating to each tea.
Some other information is given below:
1. Cup 6 contained tea from Himachal.
2. Tea from Ooty got the highest rating, but it was not in Cup 3.
3. The rating of tea in Cup 3 was double the rating of the tea in Cup 5.
4. Only two cups got ratings in even numbers.
5. Cup 2 got the minimum rating and this rating was an even number.
6. Tea in Cup 3 got a higher rating than that in Cup 1.
7. The rating of tea from Wayanad was more than the rating of tea from Munnar, but less than that from Assam.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
A tea taster was assigned to rate teas from six different locations - Munnar, Wayanad, Ooty, Darjeeling, Assam and Himachal. These teas were placed in six cups, numbered 1 to 6, not necessarily in the same order. The tea taster was asked to rate these teas on the strength of their flavour on a scale of 1 to 10. He gave a unique integer rating to each tea.
Some other information is given below:
1. Cup 6 contained tea from Himachal.
2. Tea from Ooty got the highest rating, but it was not in Cup 3.
3. The rating of tea in Cup 3 was double the rating of the tea in Cup 5.
4. Only two cups got ratings in even numbers.
5. Cup 2 got the minimum rating and this rating was an even number.
6. Tea in Cup 3 got a higher rating than that in Cup 1.
7. The rating of tea from Wayanad was more than the rating of tea from Munnar, but less than that from Assam.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
A tea taster was assigned to rate teas from six different locations - Munnar, Wayanad, Ooty, Darjeeling, Assam and Himachal. These teas were placed in six cups, numbered 1 to 6, not necessarily in the same order. The tea taster was asked to rate these teas on the strength of their flavour on a scale of 1 to 10. He gave a unique integer rating to each tea.
Some other information is given below:
1. Cup 6 contained tea from Himachal.
2. Tea from Ooty got the highest rating, but it was not in Cup 3.
3. The rating of tea in Cup 3 was double the rating of the tea in Cup 5.
4. Only two cups got ratings in even numbers.
5. Cup 2 got the minimum rating and this rating was an even number.
6. Tea in Cup 3 got a higher rating than that in Cup 1.
7. The rating of tea from Wayanad was more than the rating of tea from Munnar, but less than that from Assam.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
A tea taster was assigned to rate teas from six different locations - Munnar, Wayanad, Ooty, Darjeeling, Assam and Himachal. These teas were placed in six cups, numbered 1 to 6, not necessarily in the same order. The tea taster was asked to rate these teas on the strength of their flavour on a scale of 1 to 10. He gave a unique integer rating to each tea.
Some other information is given below:
1. Cup 6 contained tea from Himachal.
2. Tea from Ooty got the highest rating, but it was not in Cup 3.
3. The rating of tea in Cup 3 was double the rating of the tea in Cup 5.
4. Only two cups got ratings in even numbers.
5. Cup 2 got the minimum rating and this rating was an even number.
6. Tea in Cup 3 got a higher rating than that in Cup 1.
7. The rating of tea from Wayanad was more than the rating of tea from Munnar, but less than that from Assam.
Comprehension
Directions for Questions : Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark (1) if the question can be answered by using the statement A alone but not by using the statement B alone.
Mark (2) if the question can be answered by using the statement B alone but not by using the statement A alone.
Mark (3) if the question can be answered by using either of the statements alone.
Mark (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark (5) if the question cannot be answered on the basis of the two statements
CAT/2007(DILR)
Question. 141
In a particular school, sixty students were athletes. Ten among them were also among the top academic performers. How many top academic performers were in the school? A. Sixty per cent of the top academic performers were not athletes. B. All the top academic performers were not necessarily athletes.
Comprehension
Directions for Questions : Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark (1) if the question can be answered by using the statement A alone but not by using the statement B alone.
Mark (2) if the question can be answered by using the statement B alone but not by using the statement A alone.
Mark (3) if the question can be answered by using either of the statements alone.
Mark (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark (5) if the question cannot be answered on the basis of the two statements
CAT/2007(DILR)
Question. 142
Five students Atul, Bala, Chetan, Dev and Ernesto were the only ones who participated in a quiz contest. They were ranked based on their scores in the contest. Dev got a higher rank as compared to Ernesto, while Bala got a higher rank as compared to Chetan. Chetan’s rank was lower than the median. Who among the five got the highest rank?
A. Atul was the last rank holder.
B. Bala was not among the top two rank holders.
Comprehension
Directions for Questions : Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark (1) if the question can be answered by using the statement A alone but not by using the statement B alone.
Mark (2) if the question can be answered by using the statement B alone but not by using the statement A alone.
Mark (3) if the question can be answered by using either of the statements alone.
Mark (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark (5) if the question cannot be answered on the basis of the two statements
CAT/2007(DILR)
Question. 143
Thirty per cent of the employees of a call centre are males. Ten per cent of the female employees have an engineering background. What is the percentage of male employees with engineering background?
A. Twenty five per cent of the employees have engineering background.
B. Number of male employees having an engineering background is 20% more than the number of female employees having an engineering background.
Comprehension
Directions for Questions : Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark (1) if the question can be answered by using the statement A alone but not by using the statement B alone.
Mark (2) if the question can be answered by using the statement B alone but not by using the statement A alone.
Mark (3) if the question can be answered by using either of the statements alone.
Mark (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark (5) if the question cannot be answered on the basis of the two statements
CAT/2007(DILR)
Question. 144
ln a football match, at the half-time, Mahindra and Mahindra Club was trailing by three goals. Did it win the match? A. In the second-half Mahindra and Mahindra Club scored four goals. B. The opponent scored four goals in the match.
Comprehension
Directions for Questions: Answer the following questions based on the information given below:
The following table shows the break-up of actual costs incurred by a company in last five years (year 2002 to year 2006) to produce a particular product:
The production capacity of the company is 2000 units. The selling price for the year 2006 was Rs. 125 per unit. Some costs change almost in direct proportion to the change in volume of production, while others do not follow any obvious pattern of change with respect to the volume of production and hence are considered fixed. Using the information provided for the year 2006 as the basis for projecting the figures for the year 2007, answer the following questions:
Comprehension
Directions for Questions: Answer the following questions based on the information given below:
The following table shows the break-up of actual costs incurred by a company in last five years (year 2002 to year 2006) to produce a particular product:

The production capacity of the company is 2000 units. The selling price for the year 2006 was Rs. 125 per unit. Some costs change almost in direct proportion to the change in volume of production, while others do not follow any obvious pattern of change with respect to the volume of production and hence are considered fixed. Using the information provided for the year 2006 as the basis for projecting the figures for the year 2007, answer the following questions:
Comprehension
Directions for Questions: Answer the following questions based on the information given below:
The following table shows the break-up of actual costs incurred by a company in last five years (year 2002 to year 2006) to produce a particular product:

The production capacity of the company is 2000 units. The selling price for the year 2006 was Rs. 125 per unit. Some costs change almost in direct proportion to the change in volume of production, while others do not follow any obvious pattern of change with respect to the volume of production and hence are considered fixed. Using the information provided for the year 2006 as the basis for projecting the figures for the year 2007, answer the following questions:
Comprehension
Directions for Questions: Answer the following questions based on the information given below:
The following table shows the break-up of actual costs incurred by a company in last five years (year 2002 to year 2006) to produce a particular product:

The production capacity of the company is 2000 units. The selling price for the year 2006 was Rs. 125 per unit. Some costs change almost in direct proportion to the change in volume of production, while others do not follow any obvious pattern of change with respect to the volume of production and hence are considered fixed. Using the information provided for the year 2006 as the basis for projecting the figures for the year 2007, answer the following questions:
Comprehension
Directions for questions: Read the information given below and answer the questions that follow :
There are three vessels A, B and C with capacities 5, 3 and 2 respectively. There is a computer program that can perform certain functions as described below:
Drain (Y) : drains the liquid in a vessel Y.
Fill (X, Y) : fill amount from Y into X such that the amount of liquid withdrawn from Y is equal to the liquid in X.
Empty (X,Y) : empty amount from Y into X such that the amount left in Y is equal to the amount of liquid in X.
Comprehension
Directions for questions: Read the information given below and answer the questions that follow :
There are three vessels A, B and C with capacities 5, 3 and 2 respectively. There is a computer program that can perform certain functions as described below:
Drain (Y) : drains the liquid in a vessel Y.
Fill (X, Y) : fill amount from Y into X such that the amount of liquid withdrawn from Y is equal to the liquid in X.
Empty (X,Y) : empty amount from Y into X such that the amount left in Y is equal to the amount of liquid in X.
Comprehension
Directions for Questions : A robot moves on a co-ordinate plane as per the following instructions :

Comprehension
Directions for Questions : A robot moves on a co-ordinate plane as per the following instructions :

Comprehension
Directions for Questions : A robot moves on a co-ordinate plane as per the following instructions :
