CAT DILR Questions | CAT Analytical Reasoning questions
This section contains CAT Past Year Questions based on ANALYTICAL REASONING — Arrangement; Conditional Analysis; Relationships and Associations; Categorisation; Optimisation; Mathematical Reasoning; Decision Making. CAT Analytical Reasoning | CAT Past Year DILR QuestionsComprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.

Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.

Comprehension
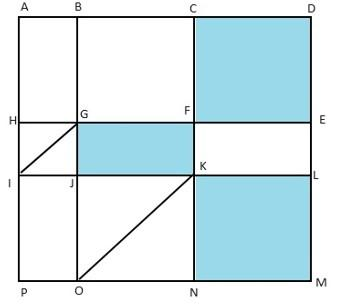
The above is a schematic diagram of walkways (indicated by all the straight-lines) and lakes (3 of them, each in the shape of rectangles – shaded in the diagram) of a gated area. Different points on the walkway are indicated by letters (A through P) with distances being OP = 150 m, ON = MN = 300 m, ML = 400 m, EL = 200 m, DE = 400 m.
The following additional information about the facilities in the area is known.
1. The only entry/exit point is at C.
2. There are many residences within the gated area; all of them are located on the path AH and ML with four of them being at A, H, M, and L.
3. The post office is located at P and the bank is located at B.
Comprehension

The above is a schematic diagram of walkways (indicated by all the straight-lines) and lakes (3 of them, each in the shape of rectangles – shaded in the diagram) of a gated area. Different points on the walkway are indicated by letters (A through P) with distances being OP = 150 m, ON = MN = 300 m, ML = 400 m, EL = 200 m, DE = 400 m.
The following additional information about the facilities in the area is known.
1. The only entry/exit point is at C.
2. There are many residences within the gated area; all of them are located on the path AH and ML with four of them being at A, H, M, and L.
3. The post office is located at P and the bank is located at B.
CAT/2024.2(DILR)
Question. 7
One person enters the gated area and decides to walk as much as possible before leaving the area without walking along any path more than once and always walking next to one of the lakes. Note that he may cross a point multiple times. How much distance (in m) will he walk within the gated area?
Comprehension

The above is a schematic diagram of walkways (indicated by all the straight-lines) and lakes (3 of them, each in the shape of rectangles – shaded in the diagram) of a gated area. Different points on the walkway are indicated by letters (A through P) with distances being OP = 150 m, ON = MN = 300 m, ML = 400 m, EL = 200 m, DE = 400 m.
The following additional information about the facilities in the area is known.
1. The only entry/exit point is at C.
2. There are many residences within the gated area; all of them are located on the path AH and ML with four of them being at A, H, M, and L.
3. The post office is located at P and the bank is located at B.
CAT/2024.2(DILR)
Question. 8
One resident takes a walk within the gated area starting from A and returning to A without going through any point (other than A) more than once. What is the maximum distance (in m) she can walk in this way?
5100
Comprehension

The above is a schematic diagram of walkways (indicated by all the straight-lines) and lakes (3 of them, each in the shape of rectangles – shaded in the diagram) of a gated area. Different points on the walkway are indicated by letters (A through P) with distances being OP = 150 m, ON = MN = 300 m, ML = 400 m, EL = 200 m, DE = 400 m.
The following additional information about the facilities in the area is known.
1. The only entry/exit point is at C.
2. There are many residences within the gated area; all of them are located on the path AH and ML with four of them being at A, H, M, and L.
3. The post office is located at P and the bank is located at B.
CAT/2024.2(DILR)
Question. 9
Visitors coming for morning walks are allowed to enter as long as they do not pass by any of the residences and do not cross any point (except C) more than once. What is the maximum distance (in m) that such a visitor can walk within the gated area?
3500
Comprehension
Eight gymnastics players numbered 1 through 8 underwent a training camp where they were coached by three coaches - Xena, Yuki, and Zara. Each coach trained at least two players. Yuki trained only even numbered players, while Zara trained only odd numbered players. After the camp, the coaches evaluated the players and gave integer ratings to the respective players trained by them on a scale of 1 to 7, with 1 being the lowest rating and 7 the highest.
The following additional information is known.
1. Xena trained more players than Yuki.
2. Player-1 and Player-4 were trained by the same coach, while the coaches who trained Player-2, Player-3 and Player-5 were all different.
3. Player-5 and Player-7 were trained by the same coach and got the same rating. All other players got a unique rating.
4. The average of the ratings of all the players was 4.
5. Player-2 got the highest rating.
6. The average of the ratings of the players trained by Yuki was twice that of the players trained by Xena and two more than that of the players trained by Zara.
7. Player-4's rating was double of Player-8's and less than Player-5's.
Comprehension
Eight gymnastics players numbered 1 through 8 underwent a training camp where they were coached by three coaches - Xena, Yuki, and Zara. Each coach trained at least two players. Yuki trained only even numbered players, while Zara trained only odd numbered players. After the camp, the coaches evaluated the players and gave integer ratings to the respective players trained by them on a scale of 1 to 7, with 1 being the lowest rating and 7 the highest.
The following additional information is known.
1. Xena trained more players than Yuki.
2. Player-1 and Player-4 were trained by the same coach, while the coaches who trained Player-2, Player-3 and Player-5 were all different.
3. Player-5 and Player-7 were trained by the same coach and got the same rating. All other players got a unique rating.
4. The average of the ratings of all the players was 4.
5. Player-2 got the highest rating.
6. The average of the ratings of the players trained by Yuki was twice that of the players trained by Xena and two more than that of the players trained by Zara.
7. Player-4's rating was double of Player-8's and less than Player-5's.
Comprehension
Eight gymnastics players numbered 1 through 8 underwent a training camp where they were coached by three coaches - Xena, Yuki, and Zara. Each coach trained at least two players. Yuki trained only even numbered players, while Zara trained only odd numbered players. After the camp, the coaches evaluated the players and gave integer ratings to the respective players trained by them on a scale of 1 to 7, with 1 being the lowest rating and 7 the highest.
The following additional information is known.
1. Xena trained more players than Yuki.
2. Player-1 and Player-4 were trained by the same coach, while the coaches who trained Player-2, Player-3 and Player-5 were all different.
3. Player-5 and Player-7 were trained by the same coach and got the same rating. All other players got a unique rating.
4. The average of the ratings of all the players was 4.
5. Player-2 got the highest rating.
6. The average of the ratings of the players trained by Yuki was twice that of the players trained by Xena and two more than that of the players trained by Zara.
7. Player-4's rating was double of Player-8's and less than Player-5's.
Comprehension
Eight gymnastics players numbered 1 through 8 underwent a training camp where they were coached by three coaches - Xena, Yuki, and Zara. Each coach trained at least two players. Yuki trained only even numbered players, while Zara trained only odd numbered players. After the camp, the coaches evaluated the players and gave integer ratings to the respective players trained by them on a scale of 1 to 7, with 1 being the lowest rating and 7 the highest.
The following additional information is known.
1. Xena trained more players than Yuki.
2. Player-1 and Player-4 were trained by the same coach, while the coaches who trained Player-2, Player-3 and Player-5 were all different.
3. Player-5 and Player-7 were trained by the same coach and got the same rating. All other players got a unique rating.
4. The average of the ratings of all the players was 4.
5. Player-2 got the highest rating.
6. The average of the ratings of the players trained by Yuki was twice that of the players trained by Xena and two more than that of the players trained by Zara.
7. Player-4's rating was double of Player-8's and less than Player-5's.
Comprehension
Eight gymnastics players numbered 1 through 8 underwent a training camp where they were coached by three coaches - Xena, Yuki, and Zara. Each coach trained at least two players. Yuki trained only even numbered players, while Zara trained only odd numbered players. After the camp, the coaches evaluated the players and gave integer ratings to the respective players trained by them on a scale of 1 to 7, with 1 being the lowest rating and 7 the highest.
The following additional information is known.
1. Xena trained more players than Yuki.
2. Player-1 and Player-4 were trained by the same coach, while the coaches who trained Player-2, Player-3 and Player-5 were all different.
3. Player-5 and Player-7 were trained by the same coach and got the same rating. All other players got a unique rating.
4. The average of the ratings of all the players was 4.
5. Player-2 got the highest rating.
6. The average of the ratings of the players trained by Yuki was twice that of the players trained by Xena and two more than that of the players trained by Zara.
7. Player-4's rating was double of Player-8's and less than Player-5's.
Comprehension
The numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 are placed in ten slots of the following grid based on the conditions below.
1. Numbers in any row appear in an increasing order from left to right.
2. Numbers in any column appear in a decreasing order from top to bottom.
3. 1 is placed either in the same row or in the same column as 10.
4. Neither 2 nor 3 is placed in the same row or in the same column as 10.
5. Neither 7 nor 8 is placed in the same row or in the same column as 9.
6. 4 and 6 are placed in the same row.
Comprehension
The numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 are placed in ten slots of the following grid based on the conditions below.
1. Numbers in any row appear in an increasing order from left to right.
2. Numbers in any column appear in a decreasing order from top to bottom.
3. 1 is placed either in the same row or in the same column as 10.
4. Neither 2 nor 3 is placed in the same row or in the same column as 10.
5. Neither 7 nor 8 is placed in the same row or in the same column as 9.
6. 4 and 6 are placed in the same row.
Comprehension
The numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 are placed in ten slots of the following grid based on the conditions below.
1. Numbers in any row appear in an increasing order from left to right.
2. Numbers in any column appear in a decreasing order from top to bottom.
3. 1 is placed either in the same row or in the same column as 10.
4. Neither 2 nor 3 is placed in the same row or in the same column as 10.
5. Neither 7 nor 8 is placed in the same row or in the same column as 9.
6. 4 and 6 are placed in the same row.
Comprehension
The numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 are placed in ten slots of the following grid based on the conditions below.
1. Numbers in any row appear in an increasing order from left to right.
2. Numbers in any column appear in a decreasing order from top to bottom.
3. 1 is placed either in the same row or in the same column as 10.
4. Neither 2 nor 3 is placed in the same row or in the same column as 10.
5. Neither 7 nor 8 is placed in the same row or in the same column as 9.
6. 4 and 6 are placed in the same row.
Comprehension
The numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 are placed in ten slots of the following grid based on the conditions below.
1. Numbers in any row appear in an increasing order from left to right.
2. Numbers in any column appear in a decreasing order from top to bottom.
3. 1 is placed either in the same row or in the same column as 10.
4. Neither 2 nor 3 is placed in the same row or in the same column as 10.
5. Neither 7 nor 8 is placed in the same row or in the same column as 9.
6. 4 and 6 are placed in the same row.
26
Comprehension
An online e-commerce firm receives daily integer product ratings from 1 through 5 given by buyers. The daily average is the average of the ratings given on that day. The cumulative average is the average of all ratings given on or before that day.
The rating system began on Day 1, and the cumulative averages were 3 and 3.1 at the end of Day 1 and Day 2, respectively. The distribution of ratings on Day 2 is given in the figure below.
The following information is known about ratings on Day 3.
1. 100 buyers gave product ratings on Day 3.
2. The modes of the product ratings were 4 and 5.
3. The numbers of buyers giving each product rating are non-zero multiples of 10.
4. The same number of buyers gave product ratings of 1 and 2, and that number is half the number of buyers who gave a rating of 3.
150
Comprehension
An online e-commerce firm receives daily integer product ratings from 1 through 5 given by buyers. The daily average is the average of the ratings given on that day. The cumulative average is the average of all ratings given on or before that day.
The rating system began on Day 1, and the cumulative averages were 3 and 3.1 at the end of Day 1 and Day 2, respectively. The distribution of ratings on Day 2 is given in the figure below.
The following information is known about ratings on Day 3.
1. 100 buyers gave product ratings on Day 3.
2. The modes of the product ratings were 4 and 5.
3. The numbers of buyers giving each product rating are non-zero multiples of 10.
4. The same number of buyers gave product ratings of 1 and 2, and that number is half the number of buyers who gave a rating of 3.
Comprehension
An online e-commerce firm receives daily integer product ratings from 1 through 5 given by buyers. The daily average is the average of the ratings given on that day. The cumulative average is the average of all ratings given on or before that day.
The rating system began on Day 1, and the cumulative averages were 3 and 3.1 at the end of Day 1 and Day 2, respectively. The distribution of ratings on Day 2 is given in the figure below.
The following information is known about ratings on Day 3.
1. 100 buyers gave product ratings on Day 3.
2. The modes of the product ratings were 4 and 5.
3. The numbers of buyers giving each product rating are non-zero multiples of 10.
4. The same number of buyers gave product ratings of 1 and 2, and that number is half the number of buyers who gave a rating of 3.
Comprehension
An online e-commerce firm receives daily integer product ratings from 1 through 5 given by buyers. The daily average is the average of the ratings given on that day. The cumulative average is the average of all ratings given on or before that day.
The rating system began on Day 1, and the cumulative averages were 3 and 3.1 at the end of Day 1 and Day 2, respectively. The distribution of ratings on Day 2 is given in the figure below.
The following information is known about ratings on Day 3.
1. 100 buyers gave product ratings on Day 3.
2. The modes of the product ratings were 4 and 5.
3. The numbers of buyers giving each product rating are non-zero multiples of 10.
4. The same number of buyers gave product ratings of 1 and 2, and that number is half the number of buyers who gave a rating of 3.
CAT/2024.2(DILR)
Question. 23
Which of the following is true about the cumulative average ratings of Day 2 and Day 3?
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
Every day a widget supplier supplies widgets from the warehouse (W) to four locations – Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands and corresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.
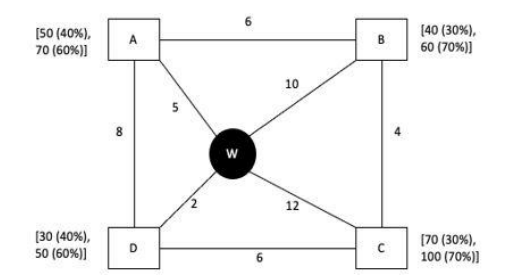
Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.
CAT/2022.2(DILR)
Question. 24
If the last location visited is Ahmednagar, then what is the total distance covered in the route (in km)?
35
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
Every day a widget supplier supplies widgets from the warehouse (W) to four locations – Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands and corresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.

Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.
CAT/2022.2(DILR)
Question. 25
If the total number of widgets delivered in a day is 250 units, then what is the total distance covered in the route (in km)?
38
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
Every day a widget supplier supplies widgets from the warehouse (W) to four locations – Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands and corresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.

Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.
CAT/2022.2(DILR)
Question. 26
What is the chance that the total number of widgets delivered in a day is 260 units and the route ends at Bikrampore?
38
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
Every day a widget supplier supplies widgets from the warehouse (W) to four locations – Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands and corresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.

Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
Every day a widget supplier supplies widgets from the warehouse (W) to four locations – Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands and corresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.

Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
Adhara, Bithi, Chhaya, Dhanavi, Esther, and Fathima are the interviewers in a process that awards funding for new initiatives. Every interviewer individually interviews each of the candidates individually and awards a token only if she recommends funding. A token has a face value of 2, 3, 5, 7, 11, or 13. Each interviewer awards tokens of a single face value only. Once all six interviews are over for a candidate, the candidate receives a funding that is Rs.1000 times the product of the face values of all the tokens. For example, if a candidate has tokens with face values 2, 5, and 7, then they get a funding of Rs.1000 × (2 × 5 × 7) = Rs.70,000. Pragnyaa, Qahira, Rasheeda, Smera, and Tantra were five candidates who received funding. The funds they received, in descending order, were Rs.390,000, Rs.210,000, Rs.165,000, Rs.77,000, and Rs.66,000. The following additional facts are known:
1. Fathima awarded tokens to everyone except Qahira, while Adhara awarded tokens to no one except Pragnyaa.
2. Rashida received the highest number of tokens that anyone received, but she did not receive one from Esther.
3. Bithi awarded a token to Smera but not to Qahira, while Dhanavi awarded a token to Qahira but not to Smera.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
Adhara, Bithi, Chhaya, Dhanavi, Esther, and Fathima are the interviewers in a process that awards funding for new initiatives. Every interviewer individually interviews each of the candidates individually and awards a token only if she recommends funding. A token has a face value of 2, 3, 5, 7, 11, or 13. Each interviewer awards tokens of a single face value only. Once all six interviews are over for a candidate, the candidate receives a funding that is Rs.1000 times the product of the face values of all the tokens. For example, if a candidate has tokens with face values 2, 5, and 7, then they get a funding of Rs.1000 × (2 × 5 × 7) = Rs.70,000. Pragnyaa, Qahira, Rasheeda, Smera, and Tantra were five candidates who received funding. The funds they received, in descending order, were Rs.390,000, Rs.210,000, Rs.165,000, Rs.77,000, and Rs.66,000. The following additional facts are known:
1. Fathima awarded tokens to everyone except Qahira, while Adhara awarded tokens to no one except Pragnyaa.
2. Rashida received the highest number of tokens that anyone received, but she did not receive one from Esther.
3. Bithi awarded a token to Smera but not to Qahira, while Dhanavi awarded a token to Qahira but not to Smera.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
Adhara, Bithi, Chhaya, Dhanavi, Esther, and Fathima are the interviewers in a process that awards funding for new initiatives. Every interviewer individually interviews each of the candidates individually and awards a token only if she recommends funding. A token has a face value of 2, 3, 5, 7, 11, or 13. Each interviewer awards tokens of a single face value only. Once all six interviews are over for a candidate, the candidate receives a funding that is Rs.1000 times the product of the face values of all the tokens. For example, if a candidate has tokens with face values 2, 5, and 7, then they get a funding of Rs.1000 × (2 × 5 × 7) = Rs.70,000. Pragnyaa, Qahira, Rasheeda, Smera, and Tantra were five candidates who received funding. The funds they received, in descending order, were Rs.390,000, Rs.210,000, Rs.165,000, Rs.77,000, and Rs.66,000. The following additional facts are known:
1. Fathima awarded tokens to everyone except Qahira, while Adhara awarded tokens to no one except Pragnyaa.
2. Rashida received the highest number of tokens that anyone received, but she did not receive one from Esther.
3. Bithi awarded a token to Smera but not to Qahira, while Dhanavi awarded a token to Qahira but not to Smera.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
Adhara, Bithi, Chhaya, Dhanavi, Esther, and Fathima are the interviewers in a process that awards funding for new initiatives. Every interviewer individually interviews each of the candidates individually and awards a token only if she recommends funding. A token has a face value of 2, 3, 5, 7, 11, or 13. Each interviewer awards tokens of a single face value only. Once all six interviews are over for a candidate, the candidate receives a funding that is Rs.1000 times the product of the face values of all the tokens. For example, if a candidate has tokens with face values 2, 5, and 7, then they get a funding of Rs.1000 × (2 × 5 × 7) = Rs.70,000. Pragnyaa, Qahira, Rasheeda, Smera, and Tantra were five candidates who received funding. The funds they received, in descending order, were Rs.390,000, Rs.210,000, Rs.165,000, Rs.77,000, and Rs.66,000. The following additional facts are known:
1. Fathima awarded tokens to everyone except Qahira, while Adhara awarded tokens to no one except Pragnyaa.
2. Rashida received the highest number of tokens that anyone received, but she did not receive one from Esther.
3. Bithi awarded a token to Smera but not to Qahira, while Dhanavi awarded a token to Qahira but not to Smera.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
Adhara, Bithi, Chhaya, Dhanavi, Esther, and Fathima are the interviewers in a process that awards funding for new initiatives. Every interviewer individually interviews each of the candidates individually and awards a token only if she recommends funding. A token has a face value of 2, 3, 5, 7, 11, or 13. Each interviewer awards tokens of a single face value only. Once all six interviews are over for a candidate, the candidate receives a funding that is Rs.1000 times the product of the face values of all the tokens. For example, if a candidate has tokens with face values 2, 5, and 7, then they get a funding of Rs.1000 × (2 × 5 × 7) = Rs.70,000. Pragnyaa, Qahira, Rasheeda, Smera, and Tantra were five candidates who received funding. The funds they received, in descending order, were Rs.390,000, Rs.210,000, Rs.165,000, Rs.77,000, and Rs.66,000. The following additional facts are known:
1. Fathima awarded tokens to everyone except Qahira, while Adhara awarded tokens to no one except Pragnyaa.
2. Rashida received the highest number of tokens that anyone received, but she did not receive one from Esther.
3. Bithi awarded a token to Smera but not to Qahira, while Dhanavi awarded a token to Qahira but not to Smera.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
There are 15 girls and some boys among the graduating students in a class. They are planning a get-together, which can be either a 1-day event, or a 2-day event, or a 3-day event. There are 6 singers in the class, 4 of them are boys. There are 10 dancers in the class, 4 of them are girls. No dancer in the class is a singer. Some students are not interested in attending the get-together. Those students who are interested in attending a 3-day event are also interested in attending a 2-day event; those who are interested in attending a 2-day event are also interested in attending a 1-day event. The following facts are also known:
1. All the girls and 80% of the boys are interested in attending a 1-day event. 60% of the boys are interested in attending a 2-day event.
2. Some of the girls are interested in attending a 1-day event, but not a 2-day event; some of the other girls are interested in attending both.
3. 70% of the boys who are interested in attending a 2-day event are neither singers nor dancers. 60% of the girls who are interested in attending a 2-day event are neither singers nor dancers.
4. No girl is interested in attending a 3-day event. All male singers and 2 of the dancers are interested in attending a 3-day event.
5. The number of singers interested in attending a 2-day event is one more than the number of dancers interested in attending a 2-day event.
50
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
There are 15 girls and some boys among the graduating students in a class. They are planning a get-together, which can be either a 1-day event, or a 2-day event, or a 3-day event. There are 6 singers in the class, 4 of them are boys. There are 10 dancers in the class, 4 of them are girls. No dancer in the class is a singer. Some students are not interested in attending the get-together. Those students who are interested in attending a 3-day event are also interested in attending a 2-day event; those who are interested in attending a 2-day event are also interested in attending a 1-day event. The following facts are also known:
1. All the girls and 80% of the boys are interested in attending a 1-day event. 60% of the boys are interested in attending a 2-day event.
2. Some of the girls are interested in attending a 1-day event, but not a 2-day event; some of the other girls are interested in attending both.
3. 70% of the boys who are interested in attending a 2-day event are neither singers nor dancers. 60% of the girls who are interested in attending a 2-day event are neither singers nor dancers.
4. No girl is interested in attending a 3-day event. All male singers and 2 of the dancers are interested in attending a 3-day event.
5. The number of singers interested in attending a 2-day event is one more than the number of dancers interested in attending a 2-day event.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
There are 15 girls and some boys among the graduating students in a class. They are planning a get-together, which can be either a 1-day event, or a 2-day event, or a 3-day event. There are 6 singers in the class, 4 of them are boys. There are 10 dancers in the class, 4 of them are girls. No dancer in the class is a singer. Some students are not interested in attending the get-together. Those students who are interested in attending a 3-day event are also interested in attending a 2-day event; those who are interested in attending a 2-day event are also interested in attending a 1-day event. The following facts are also known:
1. All the girls and 80% of the boys are interested in attending a 1-day event. 60% of the boys are interested in attending a 2-day event.
2. Some of the girls are interested in attending a 1-day event, but not a 2-day event; some of the other girls are interested in attending both.
3. 70% of the boys who are interested in attending a 2-day event are neither singers nor dancers. 60% of the girls who are interested in attending a 2-day event are neither singers nor dancers.
4. No girl is interested in attending a 3-day event. All male singers and 2 of the dancers are interested in attending a 3-day event.
5. The number of singers interested in attending a 2-day event is one more than the number of dancers interested in attending a 2-day event.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
There are 15 girls and some boys among the graduating students in a class. They are planning a get-together, which can be either a 1-day event, or a 2-day event, or a 3-day event. There are 6 singers in the class, 4 of them are boys. There are 10 dancers in the class, 4 of them are girls. No dancer in the class is a singer. Some students are not interested in attending the get-together. Those students who are interested in attending a 3-day event are also interested in attending a 2-day event; those who are interested in attending a 2-day event are also interested in attending a 1-day event. The following facts are also known:
1. All the girls and 80% of the boys are interested in attending a 1-day event. 60% of the boys are interested in attending a 2-day event.
2. Some of the girls are interested in attending a 1-day event, but not a 2-day event; some of the other girls are interested in attending both.
3. 70% of the boys who are interested in attending a 2-day event are neither singers nor dancers. 60% of the girls who are interested in attending a 2-day event are neither singers nor dancers.
4. No girl is interested in attending a 3-day event. All male singers and 2 of the dancers are interested in attending a 3-day event.
5. The number of singers interested in attending a 2-day event is one more than the number of dancers interested in attending a 2-day event.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
There are 15 girls and some boys among the graduating students in a class. They are planning a get-together, which can be either a 1-day event, or a 2-day event, or a 3-day event. There are 6 singers in the class, 4 of them are boys. There are 10 dancers in the class, 4 of them are girls. No dancer in the class is a singer. Some students are not interested in attending the get-together. Those students who are interested in attending a 3-day event are also interested in attending a 2-day event; those who are interested in attending a 2-day event are also interested in attending a 1-day event. The following facts are also known:
1. All the girls and 80% of the boys are interested in attending a 1-day event. 60% of the boys are interested in attending a 2-day event.
2. Some of the girls are interested in attending a 1-day event, but not a 2-day event; some of the other girls are interested in attending both.
3. 70% of the boys who are interested in attending a 2-day event are neither singers nor dancers. 60% of the girls who are interested in attending a 2-day event are neither singers nor dancers.
4. No girl is interested in attending a 3-day event. All male singers and 2 of the dancers are interested in attending a 3-day event.
5. The number of singers interested in attending a 2-day event is one more than the number of dancers interested in attending a 2-day event.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
The management of a university hockey team was evaluating performance of four women players - Amla, Bimla, Harita and Sarita for their possible selection in the university team for next year. For this purpose, the management was looking at the number of goals scored by them in the past 8 matches, numbered 1 through 8. The four players together had scored a total of 12 goals in these matches. In the 8 matches, each of them had scored at least one goal. No two players had scored the same total number of goals. The following facts are known about the goals scored by these four players only. All the questions refer only to the goals scored by these four players.
1. Only one goal was scored in every even numbered match.
2. Harita scored more goals than Bimla.
3. The highest goal scorer scored goals in exactly 3 matches including Match 4 and Match 8.
4. Bimla scored a goal in Match 1 and one each in three other consecutive matches.
5. An equal number of goals were scored in Match 3 and Match 7, which was different from the number of goals scored in either Match 1 or Match 5.
6. The match in which the highest number of goals was scored was unique and it was not Match 5.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
The management of a university hockey team was evaluating performance of four women players - Amla, Bimla, Harita and Sarita for their possible selection in the university team for next year. For this purpose, the management was looking at the number of goals scored by them in the past 8 matches, numbered 1 through 8. The four players together had scored a total of 12 goals in these matches. In the 8 matches, each of them had scored at least one goal. No two players had scored the same total number of goals. The following facts are known about the goals scored by these four players only. All the questions refer only to the goals scored by these four players.
1. Only one goal was scored in every even numbered match.
2. Harita scored more goals than Bimla.
3. The highest goal scorer scored goals in exactly 3 matches including Match 4 and Match 8.
4. Bimla scored a goal in Match 1 and one each in three other consecutive matches.
5. An equal number of goals were scored in Match 3 and Match 7, which was different from the number of goals scored in either Match 1 or Match 5.
6. The match in which the highest number of goals was scored was unique and it was not Match 5.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
The management of a university hockey team was evaluating performance of four women players - Amla, Bimla, Harita and Sarita for their possible selection in the university team for next year. For this purpose, the management was looking at the number of goals scored by them in the past 8 matches, numbered 1 through 8. The four players together had scored a total of 12 goals in these matches. In the 8 matches, each of them had scored at least one goal. No two players had scored the same total number of goals. The following facts are known about the goals scored by these four players only. All the questions refer only to the goals scored by these four players.
1. Only one goal was scored in every even numbered match.
2. Harita scored more goals than Bimla.
3. The highest goal scorer scored goals in exactly 3 matches including Match 4 and Match 8.
4. Bimla scored a goal in Match 1 and one each in three other consecutive matches.
5. An equal number of goals were scored in Match 3 and Match 7, which was different from the number of goals scored in either Match 1 or Match 5.
6. The match in which the highest number of goals was scored was unique and it was not Match 5.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
The management of a university hockey team was evaluating performance of four women players - Amla, Bimla, Harita and Sarita for their possible selection in the university team for next year. For this purpose, the management was looking at the number of goals scored by them in the past 8 matches, numbered 1 through 8. The four players together had scored a total of 12 goals in these matches. In the 8 matches, each of them had scored at least one goal. No two players had scored the same total number of goals. The following facts are known about the goals scored by these four players only. All the questions refer only to the goals scored by these four players.
1. Only one goal was scored in every even numbered match.
2. Harita scored more goals than Bimla.
3. The highest goal scorer scored goals in exactly 3 matches including Match 4 and Match 8.
4. Bimla scored a goal in Match 1 and one each in three other consecutive matches.
5. An equal number of goals were scored in Match 3 and Match 7, which was different from the number of goals scored in either Match 1 or Match 5.
6. The match in which the highest number of goals was scored was unique and it was not Match 5.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
The management of a university hockey team was evaluating performance of four women players - Amla, Bimla, Harita and Sarita for their possible selection in the university team for next year. For this purpose, the management was looking at the number of goals scored by them in the past 8 matches, numbered 1 through 8. The four players together had scored a total of 12 goals in these matches. In the 8 matches, each of them had scored at least one goal. No two players had scored the same total number of goals. The following facts are known about the goals scored by these four players only. All the questions refer only to the goals scored by these four players.
1. Only one goal was scored in every even numbered match.
2. Harita scored more goals than Bimla.
3. The highest goal scorer scored goals in exactly 3 matches including Match 4 and Match 8.
4. Bimla scored a goal in Match 1 and one each in three other consecutive matches.
5. An equal number of goals were scored in Match 3 and Match 7, which was different from the number of goals scored in either Match 1 or Match 5.
6. The match in which the highest number of goals was scored was unique and it was not Match 5.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
The game of Chango is a game where two people play against each other; one of them wins and the other loses, i.e., there are no drawn Chango games. 12 players participated in a Chango championship. They were divided into four groups: Group A consisted of Aruna, Azul, and Arif; Group B consisted of Brinda, Brij, and Biju; Group C consisted of Chitra, Chetan, and Chhavi; and Group D consisted of Dipen, Donna, and Deb.
Players within each group had a distinct rank going into the championship. The players have NOT been listed necessarily according to their ranks. In the group stage of the game, the second and third ranked players play against each other, and the winner of that game plays against the first ranked player of the group. The winner of this second game is considered as the winner of the group and enters a semi-final.
The winners from Groups A and B play against each other in one semi-final, while the winners from Groups C and D play against each other in the other semi-final. The winners of the two semi-finals play against each other in the final to decide the winner of the championship.
It is known that:
- Chitra did not win the championship.
- Aruna did not play against Arif. Brij did not play against Brinda.
- Aruna, Biju, Chitra, and Dipen played three games each, Azul and Chetan played two games each, and the remaining players played one game each.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
The game of Chango is a game where two people play against each other; one of them wins and the other loses, i.e., there are no drawn Chango games. 12 players participated in a Chango championship. They were divided into four groups: Group A consisted of Aruna, Azul, and Arif; Group B consisted of Brinda, Brij, and Biju; Group C consisted of Chitra, Chetan, and Chhavi; and Group D consisted of Dipen, Donna, and Deb.
Players within each group had a distinct rank going into the championship. The players have NOT been listed necessarily according to their ranks. In the group stage of the game, the second and third ranked players play against each other, and the winner of that game plays against the first ranked player of the group. The winner of this second game is considered as the winner of the group and enters a semi-final.
The winners from Groups A and B play against each other in one semi-final, while the winners from Groups C and D play against each other in the other semi-final. The winners of the two semi-finals play against each other in the final to decide the winner of the championship.
It is known that:
- Chitra did not win the championship.
- Aruna did not play against Arif. Brij did not play against Brinda.
- Aruna, Biju, Chitra, and Dipen played three games each, Azul and Chetan played two games each, and the remaining players played one game each.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
The game of Chango is a game where two people play against each other; one of them wins and the other loses, i.e., there are no drawn Chango games. 12 players participated in a Chango championship. They were divided into four groups: Group A consisted of Aruna, Azul, and Arif; Group B consisted of Brinda, Brij, and Biju; Group C consisted of Chitra, Chetan, and Chhavi; and Group D consisted of Dipen, Donna, and Deb.
Players within each group had a distinct rank going into the championship. The players have NOT been listed necessarily according to their ranks. In the group stage of the game, the second and third ranked players play against each other, and the winner of that game plays against the first ranked player of the group. The winner of this second game is considered as the winner of the group and enters a semi-final.
The winners from Groups A and B play against each other in one semi-final, while the winners from Groups C and D play against each other in the other semi-final. The winners of the two semi-finals play against each other in the final to decide the winner of the championship.
It is known that:
- Chitra did not win the championship.
- Aruna did not play against Arif. Brij did not play against Brinda.
- Aruna, Biju, Chitra, and Dipen played three games each, Azul and Chetan played two games each, and the remaining players played one game each.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
The game of Chango is a game where two people play against each other; one of them wins and the other loses, i.e., there are no drawn Chango games. 12 players participated in a Chango championship. They were divided into four groups: Group A consisted of Aruna, Azul, and Arif; Group B consisted of Brinda, Brij, and Biju; Group C consisted of Chitra, Chetan, and Chhavi; and Group D consisted of Dipen, Donna, and Deb.
Players within each group had a distinct rank going into the championship. The players have NOT been listed necessarily according to their ranks. In the group stage of the game, the second and third ranked players play against each other, and the winner of that game plays against the first ranked player of the group. The winner of this second game is considered as the winner of the group and enters a semi-final.
The winners from Groups A and B play against each other in one semi-final, while the winners from Groups C and D play against each other in the other semi-final. The winners of the two semi-finals play against each other in the final to decide the winner of the championship.
It is known that:
- Chitra did not win the championship.
- Aruna did not play against Arif. Brij did not play against Brinda.
- Aruna, Biju, Chitra, and Dipen played three games each, Azul and Chetan played two games each, and the remaining players played one game each.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
Ravi works in an online food-delivery company. After each delivery, customers rate Ravi on each of four parameters – Behaviour, Packaging, Hygiene, and Timeliness, on a scale from 1 to 9. If the total of the four rating points is 25 or more, then Ravi gets a bonus of ₹20 for that delivery. Additionally, a customer may or may not give Ravi a tip. If the customer gives a tip, it is either ₹30 or ₹50.
One day, Ravi made four deliveries - one to each of Atal, Bihari, Chirag and Deepak, and received a total of ₹120 in bonus and tips. He did not get both a bonus and a tip from the same customer.
The following additional facts are also known.
- In Timeliness, Ravi received a total of 21 points, and three of the customers gave him the same rating points in this parameter. Atal gave higher rating points than Bihari and Chirag in this parameter.
- Ravi received distinct rating points in Packaging from the four customers adding up to 29 points. Similarly, Ravi received distinct rating points in Hygiene from the four customers adding up to 26 points.
- Chirag gave the same rating points for Packaging and Hygiene.
- Among the four customers, Bihari gave the highest rating points in Packaging, and Chirag gave the highest rating points in Hygiene.
- Everyone rated Ravi between 5 and 7 in Behaviour. Unique maximum and minimum ratings in this parameter were given by Atal and Deepak respectively.
- If the customers are ranked based on ratings given by them in individual parameters, then Atal’s rank based on Packaging is the same as that based on Hygiene. This is also true for Deepak.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
Ravi works in an online food-delivery company. After each delivery, customers rate Ravi on each of four parameters – Behaviour, Packaging, Hygiene, and Timeliness, on a scale from 1 to 9. If the total of the four rating points is 25 or more, then Ravi gets a bonus of ₹20 for that delivery. Additionally, a customer may or may not give Ravi a tip. If the customer gives a tip, it is either ₹30 or ₹50.
One day, Ravi made four deliveries - one to each of Atal, Bihari, Chirag and Deepak, and received a total of ₹120 in bonus and tips. He did not get both a bonus and a tip from the same customer.
The following additional facts are also known.
- In Timeliness, Ravi received a total of 21 points, and three of the customers gave him the same rating points in this parameter. Atal gave higher rating points than Bihari and Chirag in this parameter.
- Ravi received distinct rating points in Packaging from the four customers adding up to 29 points. Similarly, Ravi received distinct rating points in Hygiene from the four customers adding up to 26 points.
- Chirag gave the same rating points for Packaging and Hygiene.
- Among the four customers, Bihari gave the highest rating points in Packaging, and Chirag gave the highest rating points in Hygiene.
- Everyone rated Ravi between 5 and 7 in Behaviour. Unique maximum and minimum ratings in this parameter were given by Atal and Deepak respectively.
- If the customers are ranked based on ratings given by them in individual parameters, then Atal’s rank based on Packaging is the same as that based on Hygiene. This is also true for Deepak.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
Ravi works in an online food-delivery company. After each delivery, customers rate Ravi on each of four parameters – Behaviour, Packaging, Hygiene, and Timeliness, on a scale from 1 to 9. If the total of the four rating points is 25 or more, then Ravi gets a bonus of ₹20 for that delivery. Additionally, a customer may or may not give Ravi a tip. If the customer gives a tip, it is either ₹30 or ₹50.
One day, Ravi made four deliveries - one to each of Atal, Bihari, Chirag and Deepak, and received a total of ₹120 in bonus and tips. He did not get both a bonus and a tip from the same customer.
The following additional facts are also known.
- In Timeliness, Ravi received a total of 21 points, and three of the customers gave him the same rating points in this parameter. Atal gave higher rating points than Bihari and Chirag in this parameter.
- Ravi received distinct rating points in Packaging from the four customers adding up to 29 points. Similarly, Ravi received distinct rating points in Hygiene from the four customers adding up to 26 points.
- Chirag gave the same rating points for Packaging and Hygiene.
- Among the four customers, Bihari gave the highest rating points in Packaging, and Chirag gave the highest rating points in Hygiene.
- Everyone rated Ravi between 5 and 7 in Behaviour. Unique maximum and minimum ratings in this parameter were given by Atal and Deepak respectively.
- If the customers are ranked based on ratings given by them in individual parameters, then Atal’s rank based on Packaging is the same as that based on Hygiene. This is also true for Deepak.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
Ravi works in an online food-delivery company. After each delivery, customers rate Ravi on each of four parameters – Behaviour, Packaging, Hygiene, and Timeliness, on a scale from 1 to 9. If the total of the four rating points is 25 or more, then Ravi gets a bonus of ₹20 for that delivery. Additionally, a customer may or may not give Ravi a tip. If the customer gives a tip, it is either ₹30 or ₹50.
One day, Ravi made four deliveries - one to each of Atal, Bihari, Chirag and Deepak, and received a total of ₹120 in bonus and tips. He did not get both a bonus and a tip from the same customer.
The following additional facts are also known.
- In Timeliness, Ravi received a total of 21 points, and three of the customers gave him the same rating points in this parameter. Atal gave higher rating points than Bihari and Chirag in this parameter.
- Ravi received distinct rating points in Packaging from the four customers adding up to 29 points. Similarly, Ravi received distinct rating points in Hygiene from the four customers adding up to 26 points.
- Chirag gave the same rating points for Packaging and Hygiene.
- Among the four customers, Bihari gave the highest rating points in Packaging, and Chirag gave the highest rating points in Hygiene.
- Everyone rated Ravi between 5 and 7 in Behaviour. Unique maximum and minimum ratings in this parameter were given by Atal and Deepak respectively.
- If the customers are ranked based on ratings given by them in individual parameters, then Atal’s rank based on Packaging is the same as that based on Hygiene. This is also true for Deepak.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
Ravi works in an online food-delivery company. After each delivery, customers rate Ravi on each of four parameters – Behaviour, Packaging, Hygiene, and Timeliness, on a scale from 1 to 9. If the total of the four rating points is 25 or more, then Ravi gets a bonus of ₹20 for that delivery. Additionally, a customer may or may not give Ravi a tip. If the customer gives a tip, it is either ₹30 or ₹50.
One day, Ravi made four deliveries - one to each of Atal, Bihari, Chirag and Deepak, and received a total of ₹120 in bonus and tips. He did not get both a bonus and a tip from the same customer.
The following additional facts are also known.
- In Timeliness, Ravi received a total of 21 points, and three of the customers gave him the same rating points in this parameter. Atal gave higher rating points than Bihari and Chirag in this parameter.
- Ravi received distinct rating points in Packaging from the four customers adding up to 29 points. Similarly, Ravi received distinct rating points in Hygiene from the four customers adding up to 26 points.
- Chirag gave the same rating points for Packaging and Hygiene.
- Among the four customers, Bihari gave the highest rating points in Packaging, and Chirag gave the highest rating points in Hygiene.
- Everyone rated Ravi between 5 and 7 in Behaviour. Unique maximum and minimum ratings in this parameter were given by Atal and Deepak respectively.
- If the customers are ranked based on ratings given by them in individual parameters, then Atal’s rank based on Packaging is the same as that based on Hygiene. This is also true for Deepak.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
Ravi works in an online food-delivery company. After each delivery, customers rate Ravi on each of four parameters – Behaviour, Packaging, Hygiene, and Timeliness, on a scale from 1 to 9. If the total of the four rating points is 25 or more, then Ravi gets a bonus of ₹20 for that delivery. Additionally, a customer may or may not give Ravi a tip. If the customer gives a tip, it is either ₹30 or ₹50.
One day, Ravi made four deliveries - one to each of Atal, Bihari, Chirag and Deepak, and received a total of ₹120 in bonus and tips. He did not get both a bonus and a tip from the same customer.
The following additional facts are also known.
- In Timeliness, Ravi received a total of 21 points, and three of the customers gave him the same rating points in this parameter. Atal gave higher rating points than Bihari and Chirag in this parameter.
- Ravi received distinct rating points in Packaging from the four customers adding up to 29 points. Similarly, Ravi received distinct rating points in Hygiene from the four customers adding up to 26 points.
- Chirag gave the same rating points for Packaging and Hygiene.
- Among the four customers, Bihari gave the highest rating points in Packaging, and Chirag gave the highest rating points in Hygiene.
- Everyone rated Ravi between 5 and 7 in Behaviour. Unique maximum and minimum ratings in this parameter were given by Atal and Deepak respectively.
- If the customers are ranked based on ratings given by them in individual parameters, then Atal’s rank based on Packaging is the same as that based on Hygiene. This is also true for Deepak.
Comprehension
Direction for the questions: Read the information carefully and answer the questions accordingly.
Three reviewers Amal, Bimal, and Komal are tasked with selecting questions from a pool of 13 questions (Q01 to Q13). Questions can be created by external “subject matter experts” (SMEs) or by one of the three reviewers. Each of the reviewers either approves or disapproves a question that is shown to them. Their decisions lead to eventual acceptance or rejection of the question in the manner described below.
If a question is created by an SME, it is reviewed first by Amal, and then by Bimal. If both of them approve the question, then the question is accepted and is not reviewed by Komal. If both disapprove the question, it is rejected and is not reviewed by Komal. If one of them approves the question and the other disapproves it, then the question is reviewed by Komal. Then the question is accepted only if she approves it.
A question created by one of the reviewers is decided upon by the other two. If a question is created by Amal, then it is first reviewed by Bimal. If Bimal approves the question, then it is accepted. Otherwise, it is reviewed by Komal. The question is then accepted only if Komal approves it. A similar process is followed for questions created by Bimal, whose questions are first reviewed by Komal, and then by Amal only if Komal disapproves it. Questions created by Komal are first reviewed by Amal, and then, if required, by Bimal.
The following facts are known about the review process after its completion.
- Q02, Q06, Q09, Q11, and Q12 were rejected and the other questions were accepted.
- Amal reviewed only Q02, Q03, Q04, Q06, Q08, Q10, Q11, and Q13.
- Bimal reviewed only Q02, Q04, Q06 through Q09, Q12, and Q13.
- Komal reviewed only Q01 through Q05, Q07, Q08, Q09, Q11, and Q12.
Comprehension
Direction for the questions: Read the information carefully and answer the questions accordingly.
Three reviewers Amal, Bimal, and Komal are tasked with selecting questions from a pool of 13 questions (Q01 to Q13). Questions can be created by external “subject matter experts” (SMEs) or by one of the three reviewers. Each of the reviewers either approves or disapproves a question that is shown to them. Their decisions lead to eventual acceptance or rejection of the question in the manner described below.
If a question is created by an SME, it is reviewed first by Amal, and then by Bimal. If both of them approve the question, then the question is accepted and is not reviewed by Komal. If both disapprove the question, it is rejected and is not reviewed by Komal. If one of them approves the question and the other disapproves it, then the question is reviewed by Komal. Then the question is accepted only if she approves it.
A question created by one of the reviewers is decided upon by the other two. If a question is created by Amal, then it is first reviewed by Bimal. If Bimal approves the question, then it is accepted. Otherwise, it is reviewed by Komal. The question is then accepted only if Komal approves it. A similar process is followed for questions created by Bimal, whose questions are first reviewed by Komal, and then by Amal only if Komal disapproves it. Questions created by Komal are first reviewed by Amal, and then, if required, by Bimal.
The following facts are known about the review process after its completion.
- Q02, Q06, Q09, Q11, and Q12 were rejected and the other questions were accepted.
- Amal reviewed only Q02, Q03, Q04, Q06, Q08, Q10, Q11, and Q13.
- Bimal reviewed only Q02, Q04, Q06 through Q09, Q12, and Q13.
- Komal reviewed only Q01 through Q05, Q07, Q08, Q09, Q11, and Q12.
Comprehension
Direction for the questions: Read the information carefully and answer the questions accordingly.
Three reviewers Amal, Bimal, and Komal are tasked with selecting questions from a pool of 13 questions (Q01 to Q13). Questions can be created by external “subject matter experts” (SMEs) or by one of the three reviewers. Each of the reviewers either approves or disapproves a question that is shown to them. Their decisions lead to eventual acceptance or rejection of the question in the manner described below.
If a question is created by an SME, it is reviewed first by Amal, and then by Bimal. If both of them approve the question, then the question is accepted and is not reviewed by Komal. If both disapprove the question, it is rejected and is not reviewed by Komal. If one of them approves the question and the other disapproves it, then the question is reviewed by Komal. Then the question is accepted only if she approves it.
A question created by one of the reviewers is decided upon by the other two. If a question is created by Amal, then it is first reviewed by Bimal. If Bimal approves the question, then it is accepted. Otherwise, it is reviewed by Komal. The question is then accepted only if Komal approves it. A similar process is followed for questions created by Bimal, whose questions are first reviewed by Komal, and then by Amal only if Komal disapproves it. Questions created by Komal are first reviewed by Amal, and then, if required, by Bimal.
The following facts are known about the review process after its completion.
- Q02, Q06, Q09, Q11, and Q12 were rejected and the other questions were accepted.
- Amal reviewed only Q02, Q03, Q04, Q06, Q08, Q10, Q11, and Q13.
- Bimal reviewed only Q02, Q04, Q06 through Q09, Q12, and Q13.
- Komal reviewed only Q01 through Q05, Q07, Q08, Q09, Q11, and Q12.
Comprehension
Direction for the questions: Read the information carefully and answer the questions accordingly.
Three reviewers Amal, Bimal, and Komal are tasked with selecting questions from a pool of 13 questions (Q01 to Q13). Questions can be created by external “subject matter experts” (SMEs) or by one of the three reviewers. Each of the reviewers either approves or disapproves a question that is shown to them. Their decisions lead to eventual acceptance or rejection of the question in the manner described below.
If a question is created by an SME, it is reviewed first by Amal, and then by Bimal. If both of them approve the question, then the question is accepted and is not reviewed by Komal. If both disapprove the question, it is rejected and is not reviewed by Komal. If one of them approves the question and the other disapproves it, then the question is reviewed by Komal. Then the question is accepted only if she approves it.
A question created by one of the reviewers is decided upon by the other two. If a question is created by Amal, then it is first reviewed by Bimal. If Bimal approves the question, then it is accepted. Otherwise, it is reviewed by Komal. The question is then accepted only if Komal approves it. A similar process is followed for questions created by Bimal, whose questions are first reviewed by Komal, and then by Amal only if Komal disapproves it. Questions created by Komal are first reviewed by Amal, and then, if required, by Bimal.
The following facts are known about the review process after its completion.
- Q02, Q06, Q09, Q11, and Q12 were rejected and the other questions were accepted.
- Amal reviewed only Q02, Q03, Q04, Q06, Q08, Q10, Q11, and Q13.
- Bimal reviewed only Q02, Q04, Q06 through Q09, Q12, and Q13.
- Komal reviewed only Q01 through Q05, Q07, Q08, Q09, Q11, and Q12.
Comprehension
Direction for the questions: Read the information carefully and answer the questions accordingly.
Three reviewers Amal, Bimal, and Komal are tasked with selecting questions from a pool of 13 questions (Q01 to Q13). Questions can be created by external “subject matter experts” (SMEs) or by one of the three reviewers. Each of the reviewers either approves or disapproves a question that is shown to them. Their decisions lead to eventual acceptance or rejection of the question in the manner described below.
If a question is created by an SME, it is reviewed first by Amal, and then by Bimal. If both of them approve the question, then the question is accepted and is not reviewed by Komal. If both disapprove the question, it is rejected and is not reviewed by Komal. If one of them approves the question and the other disapproves it, then the question is reviewed by Komal. Then the question is accepted only if she approves it.
A question created by one of the reviewers is decided upon by the other two. If a question is created by Amal, then it is first reviewed by Bimal. If Bimal approves the question, then it is accepted. Otherwise, it is reviewed by Komal. The question is then accepted only if Komal approves it. A similar process is followed for questions created by Bimal, whose questions are first reviewed by Komal, and then by Amal only if Komal disapproves it. Questions created by Komal are first reviewed by Amal, and then, if required, by Bimal.
The following facts are known about the review process after its completion.
- Q02, Q06, Q09, Q11, and Q12 were rejected and the other questions were accepted.
- Amal reviewed only Q02, Q03, Q04, Q06, Q08, Q10, Q11, and Q13.
- Bimal reviewed only Q02, Q04, Q06 through Q09, Q12, and Q13.
- Komal reviewed only Q01 through Q05, Q07, Q08, Q09, Q11, and Q12.
Comprehension
Direction for the questions: Read the information carefully and answer the questions accordingly.
Three reviewers Amal, Bimal, and Komal are tasked with selecting questions from a pool of 13 questions (Q01 to Q13). Questions can be created by external “subject matter experts” (SMEs) or by one of the three reviewers. Each of the reviewers either approves or disapproves a question that is shown to them. Their decisions lead to eventual acceptance or rejection of the question in the manner described below.
If a question is created by an SME, it is reviewed first by Amal, and then by Bimal. If both of them approve the question, then the question is accepted and is not reviewed by Komal. If both disapprove the question, it is rejected and is not reviewed by Komal. If one of them approves the question and the other disapproves it, then the question is reviewed by Komal. Then the question is accepted only if she approves it.
A question created by one of the reviewers is decided upon by the other two. If a question is created by Amal, then it is first reviewed by Bimal. If Bimal approves the question, then it is accepted. Otherwise, it is reviewed by Komal. The question is then accepted only if Komal approves it. A similar process is followed for questions created by Bimal, whose questions are first reviewed by Komal, and then by Amal only if Komal disapproves it. Questions created by Komal are first reviewed by Amal, and then, if required, by Bimal.
The following facts are known about the review process after its completion.
- Q02, Q06, Q09, Q11, and Q12 were rejected and the other questions were accepted.
- Amal reviewed only Q02, Q03, Q04, Q06, Q08, Q10, Q11, and Q13.
- Bimal reviewed only Q02, Q04, Q06 through Q09, Q12, and Q13.
- Komal reviewed only Q01 through Q05, Q07, Q08, Q09, Q11, and Q12.
Comprehension
Direction for the questions: Read the information carefully and answer the questions accordingly.
Each of the bottles mentioned in this question contains 50 ml of liquid. The liquid in any bottle can be 100% pure content (P) or can have certain amount of impurity (I). Visually it is not possible to distinguish between P and I. There is a testing device which detects impurity, as long as the percentage of impurity in the content tested is 10% or more.
For example, suppose bottle 1 contains only P, and bottle 2 contains 80% P and 20% I. If content from bottle 1 is tested, it will be found out that it contains only P. If content of bottle 2 is tested, the test will reveal that it contains some amount of I. If 10 ml of content from bottle 1 is mixed with 20 ml content from bottle 2, the test will show that the mixture has impurity, and hence we can conclude that at least one of the two bottles has I. However, if 10 ml of content from bottle 1 is mixed with 5 ml of content from bottle 2. the test will not detect any impurity in the resultant mixture.
Comprehension
Direction for the questions: Read the information carefully and answer the questions accordingly.
Each of the bottles mentioned in this question contains 50 ml of liquid. The liquid in any bottle can be 100% pure content (P) or can have certain amount of impurity (I). Visually it is not possible to distinguish between P and I. There is a testing device which detects impurity, as long as the percentage of impurity in the content tested is 10% or more.
For example, suppose bottle 1 contains only P, and bottle 2 contains 80% P and 20% I. If content from bottle 1 is tested, it will be found out that it contains only P. If content of bottle 2 is tested, the test will reveal that it contains some amount of I. If 10 ml of content from bottle 1 is mixed with 20 ml content from bottle 2, the test will show that the mixture has impurity, and hence we can conclude that at least one of the two bottles has I. However, if 10 ml of content from bottle 1 is mixed with 5 ml of content from bottle 2. the test will not detect any impurity in the resultant mixture.
CAT/2021.3(DILR)
Question. 61
There are four bottles. Each bottle is known to contain only P or only I. They will be considered to be “collectively ready for despatch” if all of them contain only P. In minimum how many tests, is it possible to ascertain whether these four bottles are “collectively ready for despatch”?
Comprehension
Direction for the questions: Read the information carefully and answer the questions accordingly.
Each of the bottles mentioned in this question contains 50 ml of liquid. The liquid in any bottle can be 100% pure content (P) or can have certain amount of impurity (I). Visually it is not possible to distinguish between P and I. There is a testing device which detects impurity, as long as the percentage of impurity in the content tested is 10% or more.
For example, suppose bottle 1 contains only P, and bottle 2 contains 80% P and 20% I. If content from bottle 1 is tested, it will be found out that it contains only P. If content of bottle 2 is tested, the test will reveal that it contains some amount of I. If 10 ml of content from bottle 1 is mixed with 20 ml content from bottle 2, the test will show that the mixture has impurity, and hence we can conclude that at least one of the two bottles has I. However, if 10 ml of content from bottle 1 is mixed with 5 ml of content from bottle 2. the test will not detect any impurity in the resultant mixture.
Comprehension
Direction for the questions: Read the information carefully and answer the questions accordingly.
Each of the bottles mentioned in this question contains 50 ml of liquid. The liquid in any bottle can be 100% pure content (P) or can have certain amount of impurity (I). Visually it is not possible to distinguish between P and I. There is a testing device which detects impurity, as long as the percentage of impurity in the content tested is 10% or more.
For example, suppose bottle 1 contains only P, and bottle 2 contains 80% P and 20% I. If content from bottle 1 is tested, it will be found out that it contains only P. If content of bottle 2 is tested, the test will reveal that it contains some amount of I. If 10 ml of content from bottle 1 is mixed with 20 ml content from bottle 2, the test will show that the mixture has impurity, and hence we can conclude that at least one of the two bottles has I. However, if 10 ml of content from bottle 1 is mixed with 5 ml of content from bottle 2. the test will not detect any impurity in the resultant mixture.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
The Humanities department of a college is planning to organize eight seminars, one for each of the eight doctoral students - A, B, C, D, E, F, G and H. Four of them are from Economics, three from Sociology and one from Anthropology department. Each student is guided by one among P, Q, R, S and T. Two students are guided by each of P, R and T, while one student is guided by each of Q and S. Each student is guided by a guide belonging to their department.
Each seminar is to be scheduled in one of four consecutive 30-minute slots starting at 9:00 am, 9:30 am, 10:00 am and 10:30 am on the same day. More than one seminars can be scheduled in a slot, provided the guide is free. Only three rooms are available and hence at the most three seminars can be scheduled in a slot. Students who are guided by the same guide must be scheduled in consecutive slots.
The following additional facts are also known.
1. Seminars by students from Economics are scheduled in each of the four slots.
2. A’s is the only seminar that is scheduled at 10:00 am. A is guided by R.
3. F is an Anthropology student whose seminar is scheduled at 10:30 am.
4. The seminar of a Sociology student is scheduled at 9:00 am.
5. B and G are both Sociology students, whose seminars are scheduled in the same slot. The seminar of an Economics student, who is guided by T, is also scheduled in the same slot.
6. P, who is guiding both B and C, has students scheduled in the first two slots.
7. A and G are scheduled in two consecutive slots.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
The Humanities department of a college is planning to organize eight seminars, one for each of the eight doctoral students - A, B, C, D, E, F, G and H. Four of them are from Economics, three from Sociology and one from Anthropology department. Each student is guided by one among P, Q, R, S and T. Two students are guided by each of P, R and T, while one student is guided by each of Q and S. Each student is guided by a guide belonging to their department.
Each seminar is to be scheduled in one of four consecutive 30-minute slots starting at 9:00 am, 9:30 am, 10:00 am and 10:30 am on the same day. More than one seminars can be scheduled in a slot, provided the guide is free. Only three rooms are available and hence at the most three seminars can be scheduled in a slot. Students who are guided by the same guide must be scheduled in consecutive slots.
The following additional facts are also known.
1. Seminars by students from Economics are scheduled in each of the four slots.
2. A’s is the only seminar that is scheduled at 10:00 am. A is guided by R.
3. F is an Anthropology student whose seminar is scheduled at 10:30 am.
4. The seminar of a Sociology student is scheduled at 9:00 am.
5. B and G are both Sociology students, whose seminars are scheduled in the same slot. The seminar of an Economics student, who is guided by T, is also scheduled in the same slot.
6. P, who is guiding both B and C, has students scheduled in the first two slots.
7. A and G are scheduled in two consecutive slots.
Comprehension
Directions for questions: Read the given instructions carefully and answer the questions accordingly.
The Humanities department of a college is planning to organize eight seminars, one for each of the eight doctoral students - A, B, C, D, E, F, G and H. Four of them are from Economics, three from Sociology and one from Anthropology department. Each student is guided by one among P, Q, R, S and T. Two students are guided by each of P, R and T, while one student is guided by each of Q and S. Each student is guided by a guide belonging to their department.
Each seminar is to be scheduled in one of four consecutive 30-minute slots starting at 9:00 am, 9:30 am, 10:00 am and 10:30 am on the same day. More than one seminars can be scheduled in a slot, provided the guide is free. Only three rooms are available and hence at the most three seminars can be scheduled in a slot. Students who are guided by the same guide must be scheduled in consecutive slots.
The following additional facts are also known.
1. Seminars by students from Economics are scheduled in each of the four slots.
2. A’s is the only seminar that is scheduled at 10:00 am. A is guided by R.
3. F is an Anthropology student whose seminar is scheduled at 10:30 am.
4. The seminar of a Sociology student is scheduled at 9:00 am.
5. B and G are both Sociology students, whose seminars are scheduled in the same slot. The seminar of an Economics student, who is guided by T, is also scheduled in the same slot.
6. P, who is guiding both B and C, has students scheduled in the first two slots.
7. A and G are scheduled in two consecutive slots.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
A farmer had a rectangular land containing 205 trees. He distributed that land among his four daughters – Abha, Bina, Chitra and Dipti by dividing the land into twelve plots along three rows (X,Y,Z) and four Columns (1,2,3,4) as shown in the figure below:
The plots in rows X, Y, Z contained mango, teak and pine trees respectively. Each plot had trees in non-zero multiples of 3 or 4 and none of the plots had the same number of trees. Each daughter got an even number of plots. In the figure, the number mentioned in top left corner of a plot is the number of trees in that plot, while the letter in the bottom right corner is the first letter of the name of the daughter who got that plot (For example, Abha got the plot in row Y and column 1 containing 21 trees). Some information in the figure got erased, but the following is known:
1. Abha got 20 trees more than Chitra but 6 trees less than Dipti.
2. The largest number of trees in a plot was 32, but it was not with Abha.
3. The number of teak trees in Column 3 was double of that in Column 2 but was half of that in Column 4.
4. Both Abha and Bina got a higher number of plots than Dipti.
5. Only Bina, Chitra and Dipti got corner plots.
6. Dipti got two adjoining plots in the same row.
7. Bina was the only one who got a plot in each row and each column.
8. Chitra and Dipti did not get plots which were adjacent to each other (either in row / column / diagonal).
9. The number of mango trees was double the number of teak trees.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
A farmer had a rectangular land containing 205 trees. He distributed that land among his four daughters – Abha, Bina, Chitra and Dipti by dividing the land into twelve plots along three rows (X,Y,Z) and four Columns (1,2,3,4) as shown in the figure below:
The plots in rows X, Y, Z contained mango, teak and pine trees respectively. Each plot had trees in non-zero multiples of 3 or 4 and none of the plots had the same number of trees. Each daughter got an even number of plots. In the figure, the number mentioned in top left corner of a plot is the number of trees in that plot, while the letter in the bottom right corner is the first letter of the name of the daughter who got that plot (For example, Abha got the plot in row Y and column 1 containing 21 trees). Some information in the figure got erased, but the following is known:
1. Abha got 20 trees more than Chitra but 6 trees less than Dipti.
2. The largest number of trees in a plot was 32, but it was not with Abha.
3. The number of teak trees in Column 3 was double of that in Column 2 but was half of that in Column 4.
4. Both Abha and Bina got a higher number of plots than Dipti.
5. Only Bina, Chitra and Dipti got corner plots.
6. Dipti got two adjoining plots in the same row.
7. Bina was the only one who got a plot in each row and each column.
8. Chitra and Dipti did not get plots which were adjacent to each other (either in row / column / diagonal).
9. The number of mango trees was double the number of teak trees.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
A farmer had a rectangular land containing 205 trees. He distributed that land among his four daughters – Abha, Bina, Chitra and Dipti by dividing the land into twelve plots along three rows (X,Y,Z) and four Columns (1,2,3,4) as shown in the figure below:
The plots in rows X, Y, Z contained mango, teak and pine trees respectively. Each plot had trees in non-zero multiples of 3 or 4 and none of the plots had the same number of trees. Each daughter got an even number of plots. In the figure, the number mentioned in top left corner of a plot is the number of trees in that plot, while the letter in the bottom right corner is the first letter of the name of the daughter who got that plot (For example, Abha got the plot in row Y and column 1 containing 21 trees). Some information in the figure got erased, but the following is known:
1. Abha got 20 trees more than Chitra but 6 trees less than Dipti.
2. The largest number of trees in a plot was 32, but it was not with Abha.
3. The number of teak trees in Column 3 was double of that in Column 2 but was half of that in Column 4.
4. Both Abha and Bina got a higher number of plots than Dipti.
5. Only Bina, Chitra and Dipti got corner plots.
6. Dipti got two adjoining plots in the same row.
7. Bina was the only one who got a plot in each row and each column.
8. Chitra and Dipti did not get plots which were adjacent to each other (either in row / column / diagonal).
9. The number of mango trees was double the number of teak trees.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
A farmer had a rectangular land containing 205 trees. He distributed that land among his four daughters – Abha, Bina, Chitra and Dipti by dividing the land into twelve plots along three rows (X,Y,Z) and four Columns (1,2,3,4) as shown in the figure below:
The plots in rows X, Y, Z contained mango, teak and pine trees respectively. Each plot had trees in non-zero multiples of 3 or 4 and none of the plots had the same number of trees. Each daughter got an even number of plots. In the figure, the number mentioned in top left corner of a plot is the number of trees in that plot, while the letter in the bottom right corner is the first letter of the name of the daughter who got that plot (For example, Abha got the plot in row Y and column 1 containing 21 trees). Some information in the figure got erased, but the following is known:
1. Abha got 20 trees more than Chitra but 6 trees less than Dipti.
2. The largest number of trees in a plot was 32, but it was not with Abha.
3. The number of teak trees in Column 3 was double of that in Column 2 but was half of that in Column 4.
4. Both Abha and Bina got a higher number of plots than Dipti.
5. Only Bina, Chitra and Dipti got corner plots.
6. Dipti got two adjoining plots in the same row.
7. Bina was the only one who got a plot in each row and each column.
8. Chitra and Dipti did not get plots which were adjacent to each other (either in row / column / diagonal).
9. The number of mango trees was double the number of teak trees.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
A farmer had a rectangular land containing 205 trees. He distributed that land among his four daughters – Abha, Bina, Chitra and Dipti by dividing the land into twelve plots along three rows (X,Y,Z) and four Columns (1,2,3,4) as shown in the figure below:
The plots in rows X, Y, Z contained mango, teak and pine trees respectively. Each plot had trees in non-zero multiples of 3 or 4 and none of the plots had the same number of trees. Each daughter got an even number of plots. In the figure, the number mentioned in top left corner of a plot is the number of trees in that plot, while the letter in the bottom right corner is the first letter of the name of the daughter who got that plot (For example, Abha got the plot in row Y and column 1 containing 21 trees). Some information in the figure got erased, but the following is known:
1. Abha got 20 trees more than Chitra but 6 trees less than Dipti.
2. The largest number of trees in a plot was 32, but it was not with Abha.
3. The number of teak trees in Column 3 was double of that in Column 2 but was half of that in Column 4.
4. Both Abha and Bina got a higher number of plots than Dipti.
5. Only Bina, Chitra and Dipti got corner plots.
6. Dipti got two adjoining plots in the same row.
7. Bina was the only one who got a plot in each row and each column.
8. Chitra and Dipti did not get plots which were adjacent to each other (either in row / column / diagonal).
9. The number of mango trees was double the number of teak trees.
Comprehension
Directions for the Questions: Read the information carefully and answer the given questions accordingly.
A farmer had a rectangular land containing 205 trees. He distributed that land among his four daughters – Abha, Bina, Chitra and Dipti by dividing the land into twelve plots along three rows (X,Y,Z) and four Columns (1,2,3,4) as shown in the figure below:
The plots in rows X, Y, Z contained mango, teak and pine trees respectively. Each plot had trees in non-zero multiples of 3 or 4 and none of the plots had the same number of trees. Each daughter got an even number of plots. In the figure, the number mentioned in top left corner of a plot is the number of trees in that plot, while the letter in the bottom right corner is the first letter of the name of the daughter who got that plot (For example, Abha got the plot in row Y and column 1 containing 21 trees). Some information in the figure got erased, but the following is known:
1. Abha got 20 trees more than Chitra but 6 trees less than Dipti.
2. The largest number of trees in a plot was 32, but it was not with Abha.
3. The number of teak trees in Column 3 was double of that in Column 2 but was half of that in Column 4.
4. Both Abha and Bina got a higher number of plots than Dipti.
5. Only Bina, Chitra and Dipti got corner plots.
6. Dipti got two adjoining plots in the same row.
7. Bina was the only one who got a plot in each row and each column.
8. Chitra and Dipti did not get plots which were adjacent to each other (either in row / column / diagonal).
9. The number of mango trees was double the number of teak trees.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
The Hi-Lo game is a four-player game played in six rounds. In every round, each player chooses to bid Hi or Lo. The bids are made simultaneously. If all four bid Hi, then all four lose 1 point each. If three players bid Hi and one bids Lo, then the players bidding Hi gain 1 point each and the player bidding Lo loses 3 points. If two players bid Hi and two bid Lo, then the players bidding Hi gain 2 points each and the players bidding Lo lose 2 points each. If one player bids Hi and three bid Lo, then the player bidding Hi gains 3 points and the players bidding Lo lose 1 point each. If all four bid Lo, then all four gain 1 point each.
Four players Arun, Bankim, Charu, and Dipak played the Hi-Lo game. The following facts are known about their game:
1. At the end of three rounds, Arun had scored 6 points, Dipak had scored 2 points, Bankim and Charu had scored -2 points each.
2. At the end of six rounds, Arun had scored 7 points, Bankim and Dipak had scored -1 point each, and Charu had scored -5 points.
3. Dipak’s score in the third round was less than his score in the first round but was more than his score in the second round.
4. In exactly two out of the six rounds, Arun was the only player who bid Hi.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
The Hi-Lo game is a four-player game played in six rounds. In every round, each player chooses to bid Hi or Lo. The bids are made simultaneously. If all four bid Hi, then all four lose 1 point each. If three players bid Hi and one bids Lo, then the players bidding Hi gain 1 point each and the player bidding Lo loses 3 points. If two players bid Hi and two bid Lo, then the players bidding Hi gain 2 points each and the players bidding Lo lose 2 points each. If one player bids Hi and three bid Lo, then the player bidding Hi gains 3 points and the players bidding Lo lose 1 point each. If all four bid Lo, then all four gain 1 point each.
Four players Arun, Bankim, Charu, and Dipak played the Hi-Lo game. The following facts are known about their game:
1. At the end of three rounds, Arun had scored 6 points, Dipak had scored 2 points, Bankim and Charu had scored -2 points each.
2. At the end of six rounds, Arun had scored 7 points, Bankim and Dipak had scored -1 point each, and Charu had scored -5 points.
3. Dipak’s score in the third round was less than his score in the first round but was more than his score in the second round.
4. In exactly two out of the six rounds, Arun was the only player who bid Hi.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
The Hi-Lo game is a four-player game played in six rounds. In every round, each player chooses to bid Hi or Lo. The bids are made simultaneously. If all four bid Hi, then all four lose 1 point each. If three players bid Hi and one bids Lo, then the players bidding Hi gain 1 point each and the player bidding Lo loses 3 points. If two players bid Hi and two bid Lo, then the players bidding Hi gain 2 points each and the players bidding Lo lose 2 points each. If one player bids Hi and three bid Lo, then the player bidding Hi gains 3 points and the players bidding Lo lose 1 point each. If all four bid Lo, then all four gain 1 point each.
Four players Arun, Bankim, Charu, and Dipak played the Hi-Lo game. The following facts are known about their game:
1. At the end of three rounds, Arun had scored 6 points, Dipak had scored 2 points, Bankim and Charu had scored -2 points each.
2. At the end of six rounds, Arun had scored 7 points, Bankim and Dipak had scored -1 point each, and Charu had scored -5 points.
3. Dipak’s score in the third round was less than his score in the first round but was more than his score in the second round.
4. In exactly two out of the six rounds, Arun was the only player who bid Hi.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
The Hi-Lo game is a four-player game played in six rounds. In every round, each player chooses to bid Hi or Lo. The bids are made simultaneously. If all four bid Hi, then all four lose 1 point each. If three players bid Hi and one bids Lo, then the players bidding Hi gain 1 point each and the player bidding Lo loses 3 points. If two players bid Hi and two bid Lo, then the players bidding Hi gain 2 points each and the players bidding Lo lose 2 points each. If one player bids Hi and three bid Lo, then the player bidding Hi gains 3 points and the players bidding Lo lose 1 point each. If all four bid Lo, then all four gain 1 point each.
Four players Arun, Bankim, Charu, and Dipak played the Hi-Lo game. The following facts are known about their game:
1. At the end of three rounds, Arun had scored 6 points, Dipak had scored 2 points, Bankim and Charu had scored -2 points each.
2. At the end of six rounds, Arun had scored 7 points, Bankim and Dipak had scored -1 point each, and Charu had scored -5 points.
3. Dipak’s score in the third round was less than his score in the first round but was more than his score in the second round.
4. In exactly two out of the six rounds, Arun was the only player who bid Hi.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
The Hi-Lo game is a four-player game played in six rounds. In every round, each player chooses to bid Hi or Lo. The bids are made simultaneously. If all four bid Hi, then all four lose 1 point each. If three players bid Hi and one bids Lo, then the players bidding Hi gain 1 point each and the player bidding Lo loses 3 points. If two players bid Hi and two bid Lo, then the players bidding Hi gain 2 points each and the players bidding Lo lose 2 points each. If one player bids Hi and three bid Lo, then the player bidding Hi gains 3 points and the players bidding Lo lose 1 point each. If all four bid Lo, then all four gain 1 point each.
Four players Arun, Bankim, Charu, and Dipak played the Hi-Lo game. The following facts are known about their game:
1. At the end of three rounds, Arun had scored 6 points, Dipak had scored 2 points, Bankim and Charu had scored -2 points each.
2. At the end of six rounds, Arun had scored 7 points, Bankim and Dipak had scored -1 point each, and Charu had scored -5 points.
3. Dipak’s score in the third round was less than his score in the first round but was more than his score in the second round.
4. In exactly two out of the six rounds, Arun was the only player who bid Hi.
Comprehension
Directions for the questions: Read the information carefully and answer the given questions accordingly.
The Hi-Lo game is a four-player game played in six rounds. In every round, each player chooses to bid Hi or Lo. The bids are made simultaneously. If all four bid Hi, then all four lose 1 point each. If three players bid Hi and one bids Lo, then the players bidding Hi gain 1 point each and the player bidding Lo loses 3 points. If two players bid Hi and two bid Lo, then the players bidding Hi gain 2 points each and the players bidding Lo lose 2 points each. If one player bids Hi and three bid Lo, then the player bidding Hi gains 3 points and the players bidding Lo lose 1 point each. If all four bid Lo, then all four gain 1 point each.
Four players Arun, Bankim, Charu, and Dipak played the Hi-Lo game. The following facts are known about their game:
1. At the end of three rounds, Arun had scored 6 points, Dipak had scored 2 points, Bankim and Charu had scored -2 points each.
2. At the end of six rounds, Arun had scored 7 points, Bankim and Dipak had scored -1 point each, and Charu had scored -5 points.
3. Dipak’s score in the third round was less than his score in the first round but was more than his score in the second round.
4. In exactly two out of the six rounds, Arun was the only player who bid Hi.
Comprehension
To compare the rainfall data, India Meteorological Department (IMD) calculated the Long Period Average (LPA) of rainfall during period June-August for each of the 16 states. The figure given below shows the actual rainfall (measured in mm) during June-August, 2019 and the percentage deviations from LPA of respective states in 2018. Each state along with its actual rainfall is presented in the figure.
Comprehension
To compare the rainfall data, India Meteorological Department (IMD) calculated the Long Period Average (LPA) of rainfall during period June-August for each of the 16 states. The figure given below shows the actual rainfall (measured in mm) during June-August, 2019 and the percentage deviations from LPA of respective states in 2018. Each state along with its actual rainfall is presented in the figure.

Comprehension
To compare the rainfall data, India Meteorological Department (IMD) calculated the Long Period Average (LPA) of rainfall during period June-August for each of the 16 states. The figure given below shows the actual rainfall (measured in mm) during June-August, 2019 and the percentage deviations from LPA of respective states in 2018. Each state along with its actual rainfall is presented in the figure.

Comprehension
To compare the rainfall data, India Meteorological Department (IMD) calculated the Long Period Average (LPA) of rainfall during period June-August for each of the 16 states. The figure given below shows the actual rainfall (measured in mm) during June-August, 2019 and the percentage deviations from LPA of respective states in 2018. Each state along with its actual rainfall is presented in the figure.

CAT/2019.2(DILR)
Question. 85
The LPA of a state for a year is defined as the average rainfall in the preceding 10 years considering the period of June-August. For example, LPA in 2018 is the average rainfall during 2009-2018 and LPA in 2019 is the average rainfall during 2010-2019. It is also observed that the actual rainfall in Gujarat in 2019 is 20% more than the rainfall in 2009. The LPA of Gujarat in 2019 is closest to
Comprehension
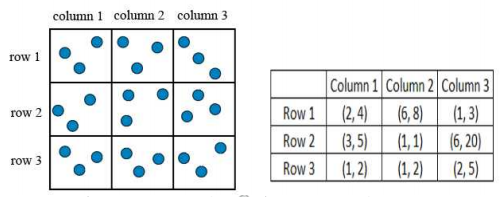
Three pouches (each represented by a filled circle) are kept in each of the nine slots in a 3 × 3 grid, as shown in the figure. Every pouch has a certain number of one-rupee coins. The minimum and maximum amounts of money (in rupees) among the three pouches in each of the nine slots are given in the table. For example, we know that among the three pouches kept in the second column of the first row, the minimum amount in a pouch is Rs. 6 and the maximum amount is Rs. 8. There are nine pouches in any of the three columns, as well as in any of the three rows. It is known that the average amount of money (in rupees) kept in the nine pouches in any column or in any row is an integer. It is also known that the total amount of money kept in the three pouches in the first column of the third row is Rs. 4.
CAT/2019.2(DILR)
Question. 86
What is the total amount of money (in rupees) in the three pouches kept in the first column of the second row?
13
Comprehension

Three pouches (each represented by a filled circle) are kept in each of the nine slots in a 3 × 3 grid, as shown in the figure. Every pouch has a certain number of one-rupee coins. The minimum and maximum amounts of money (in rupees) among the three pouches in each of the nine slots are given in the table. For example, we know that among the three pouches kept in the second column of the first row, the minimum amount in a pouch is Rs. 6 and the maximum amount is Rs. 8. There are nine pouches in any of the three columns, as well as in any of the three rows. It is known that the average amount of money (in rupees) kept in the nine pouches in any column or in any row is an integer. It is also known that the total amount of money kept in the three pouches in the first column of the third row is Rs. 4.
Comprehension

Three pouches (each represented by a filled circle) are kept in each of the nine slots in a 3 × 3 grid, as shown in the figure. Every pouch has a certain number of one-rupee coins. The minimum and maximum amounts of money (in rupees) among the three pouches in each of the nine slots are given in the table. For example, we know that among the three pouches kept in the second column of the first row, the minimum amount in a pouch is Rs. 6 and the maximum amount is Rs. 8. There are nine pouches in any of the three columns, as well as in any of the three rows. It is known that the average amount of money (in rupees) kept in the nine pouches in any column or in any row is an integer. It is also known that the total amount of money kept in the three pouches in the first column of the third row is Rs. 4.
Comprehension

Three pouches (each represented by a filled circle) are kept in each of the nine slots in a 3 × 3 grid, as shown in the figure. Every pouch has a certain number of one-rupee coins. The minimum and maximum amounts of money (in rupees) among the three pouches in each of the nine slots are given in the table. For example, we know that among the three pouches kept in the second column of the first row, the minimum amount in a pouch is Rs. 6 and the maximum amount is Rs. 8. There are nine pouches in any of the three columns, as well as in any of the three rows. It is known that the average amount of money (in rupees) kept in the nine pouches in any column or in any row is an integer. It is also known that the total amount of money kept in the three pouches in the first column of the third row is Rs. 4.
Comprehension
1600 satellites were sent up by a country for several purposes. The purposes are classified as broadcasting (B), communication (C), surveillance (S), and others (O). A satellite can serve multiple purposes; however a satellite serving either B, or C, or S does not serve O.
The following facts are known about the satellites:
1.The numbers of satellites serving B, C, and S (though may be not exclusively) are in the ratio 2:1:1.
2.The number of satellites serving all three of B, C, and S is 100.
3.The number of satellites exclusively serving C is the same as the number of satellites exclusively serving S. This number is 30% of the number of satellites exclusively serving B.
4.The number of satellites serving O is the same as the number of satellites serving both C and S but not B.
Comprehension
1600 satellites were sent up by a country for several purposes. The purposes are classified as broadcasting (B), communication (C), surveillance (S), and others (O). A satellite can serve multiple purposes; however a satellite serving either B, or C, or S does not serve O.
The following facts are known about the satellites:
1.The numbers of satellites serving B, C, and S (though may be not exclusively) are in the ratio 2:1:1.
2.The number of satellites serving all three of B, C, and S is 100.
3.The number of satellites exclusively serving C is the same as the number of satellites exclusively serving S. This number is 30% of the number of satellites exclusively serving B.
4.The number of satellites serving O is the same as the number of satellites serving both C and S but not B.
Comprehension
1600 satellites were sent up by a country for several purposes. The purposes are classified as broadcasting (B), communication (C), surveillance (S), and others (O). A satellite can serve multiple purposes; however a satellite serving either B, or C, or S does not serve O.
The following facts are known about the satellites:
1.The numbers of satellites serving B, C, and S (though may be not exclusively) are in the ratio 2:1:1.
2.The number of satellites serving all three of B, C, and S is 100.
3.The number of satellites exclusively serving C is the same as the number of satellites exclusively serving S. This number is 30% of the number of satellites exclusively serving B.
4.The number of satellites serving O is the same as the number of satellites serving both C and S but not B.
Comprehension
1600 satellites were sent up by a country for several purposes. The purposes are classified as broadcasting (B), communication (C), surveillance (S), and others (O). A satellite can serve multiple purposes; however a satellite serving either B, or C, or S does not serve O.
The following facts are known about the satellites:
1.The numbers of satellites serving B, C, and S (though may be not exclusively) are in the ratio 2:1:1.
2.The number of satellites serving all three of B, C, and S is 100.
3.The number of satellites exclusively serving C is the same as the number of satellites exclusively serving S. This number is 30% of the number of satellites exclusively serving B.
4.The number of satellites serving O is the same as the number of satellites serving both C and S but not B.
Comprehension
You are given an n×n square matrix to be filled with numerals so that no two adjacent cells have the same numeral. Two cells are called adjacent if they touch each other horizontally, vertically or diagonally. So a cell in one of the four corners has three cells adjacent to it, and a cell in the first or last row or column which is not in the corner has five cells adjacent to it. Any other cell has eight cells adjacent to it.
Comprehension
You are given an n×n square matrix to be filled with numerals so that no two adjacent cells have the same numeral. Two cells are called adjacent if they touch each other horizontally, vertically or diagonally. So a cell in one of the four corners has three cells adjacent to it, and a cell in the first or last row or column which is not in the corner has five cells adjacent to it. Any other cell has eight cells adjacent to it.
Comprehension
You are given an n×n square matrix to be filled with numerals so that no two adjacent cells have the same numeral. Two cells are called adjacent if they touch each other horizontally, vertically or diagonally. So a cell in one of the four corners has three cells adjacent to it, and a cell in the first or last row or column which is not in the corner has five cells adjacent to it. Any other cell has eight cells adjacent to it.
Comprehension
You are given an n×n square matrix to be filled with numerals so that no two adjacent cells have the same numeral. Two cells are called adjacent if they touch each other horizontally, vertically or diagonally. So a cell in one of the four corners has three cells adjacent to it, and a cell in the first or last row or column which is not in the corner has five cells adjacent to it. Any other cell has eight cells adjacent to it.
Comprehension
An ATM dispenses exactly Rs. 5000 per withdrawal using 100, 200 and 500 rupee notes. The ATM requires every customer to give her preference for one of the three denominations of notes. It then dispenses notes such that the number of notes of the customer’s preferred denomination exceeds the total number of notes of other denominations dispensed to her.
Comprehension
An ATM dispenses exactly Rs. 5000 per withdrawal using 100, 200 and 500 rupee notes. The ATM requires every customer to give her preference for one of the three denominations of notes. It then dispenses notes such that the number of notes of the customer’s preferred denomination exceeds the total number of notes of other denominations dispensed to her.
Comprehension
An ATM dispenses exactly Rs. 5000 per withdrawal using 100, 200 and 500 rupee notes. The ATM requires every customer to give her preference for one of the three denominations of notes. It then dispenses notes such that the number of notes of the customer’s preferred denomination exceeds the total number of notes of other denominations dispensed to her.
Comprehension
An ATM dispenses exactly Rs. 5000 per withdrawal using 100, 200 and 500 rupee notes. The ATM requires every customer to give her preference for one of the three denominations of notes. It then dispenses notes such that the number of notes of the customer’s preferred denomination exceeds the total number of notes of other denominations dispensed to her.
Comprehension
There are only four brands of entry level smartphones called Azra, Bysi, Cxqi, and Dipq in a country. Details about their market share, unit selling price, and profitability (defined as the profit as a percentage of the revenue) for the year 2016 are given in the table below:
In 2017, sales volume of entry level smartphones grew by 40% as compared to that in 2016. Cxqi offered a 40% discount on its unit selling price in 2017, which resulted in a 15% increase in its market share. Each of the other three brands lost 5% market share. However, the profitability of Cxqi came down to half of its value in 2016. The unit selling prices of the other three brands and their profitability values remained the same in 2017 as they were in 2016.
Comprehension
There are only four brands of entry level smartphones called Azra, Bysi, Cxqi, and Dipq in a country. Details about their market share, unit selling price, and profitability (defined as the profit as a percentage of the revenue) for the year 2016 are given in the table below:
In 2017, sales volume of entry level smartphones grew by 40% as compared to that in 2016. Cxqi offered a 40% discount on its unit selling price in 2017, which resulted in a 15% increase in its market share. Each of the other three brands lost 5% market share. However, the profitability of Cxqi came down to half of its value in 2016. The unit selling prices of the other three brands and their profitability values remained the same in 2017 as they were in 2016.
Comprehension
There are only four brands of entry level smartphones called Azra, Bysi, Cxqi, and Dipq in a country. Details about their market share, unit selling price, and profitability (defined as the profit as a percentage of the revenue) for the year 2016 are given in the table below:
In 2017, sales volume of entry level smartphones grew by 40% as compared to that in 2016. Cxqi offered a 40% discount on its unit selling price in 2017, which resulted in a 15% increase in its market share. Each of the other three brands lost 5% market share. However, the profitability of Cxqi came down to half of its value in 2016. The unit selling prices of the other three brands and their profitability values remained the same in 2017 as they were in 2016.
Comprehension
There are only four brands of entry level smartphones called Azra, Bysi, Cxqi, and Dipq in a country. Details about their market share, unit selling price, and profitability (defined as the profit as a percentage of the revenue) for the year 2016 are given in the table below:
In 2017, sales volume of entry level smartphones grew by 40% as compared to that in 2016. Cxqi offered a 40% discount on its unit selling price in 2017, which resulted in a 15% increase in its market share. Each of the other three brands lost 5% market share. However, the profitability of Cxqi came down to half of its value in 2016. The unit selling prices of the other three brands and their profitability values remained the same in 2017 as they were in 2016.
Comprehension
Each of the 23 boxes in the picture below represents a product manufactured by one of the following three companies: Alfa, Bravo and Charlie. The area of a box is proportional to the revenue from the corresponding product, while its centre represents the Product popularity and Market potential scores of the product (out of 20). The shadings of some of the boxes have got erased.
The companies classified their products into four categories based on a combination of scores (out of 20) on the two parameters - Product popularity and Market potential as given below:
The following facts are known:
1. Alfa and Bravo had the same number of products in the Blockbuster category.
2. Charlie had more products than Bravo but fewer products than Alfa in the No-hope category.
3. Each company had an equal number of products in the Promising category.
4. Charlie did not have any product in the Doubtful category, while Alfa had one product more than Bravo in this category.
5. Bravo had a higher revenue than Alfa from products in the Doubtful category.
6. Charlie had a higher revenue than Bravo from products in the Blockbuster category.
7. Bravo and Charlie had the same revenue from products in the No-hope category.
8. Alfa and Charlie had the same total revenue considering all products.
Comprehension
Each of the 23 boxes in the picture below represents a product manufactured by one of the following three companies: Alfa, Bravo and Charlie. The area of a box is proportional to the revenue from the corresponding product, while its centre represents the Product popularity and Market potential scores of the product (out of 20). The shadings of some of the boxes have got erased.
The companies classified their products into four categories based on a combination of scores (out of 20) on the two parameters - Product popularity and Market potential as given below:
The following facts are known:
1. Alfa and Bravo had the same number of products in the Blockbuster category.
2. Charlie had more products than Bravo but fewer products than Alfa in the No-hope category.
3. Each company had an equal number of products in the Promising category.
4. Charlie did not have any product in the Doubtful category, while Alfa had one product more than Bravo in this category.
5. Bravo had a higher revenue than Alfa from products in the Doubtful category.
6. Charlie had a higher revenue than Bravo from products in the Blockbuster category.
7. Bravo and Charlie had the same revenue from products in the No-hope category.
8. Alfa and Charlie had the same total revenue considering all products.
Comprehension
Each of the 23 boxes in the picture below represents a product manufactured by one of the following three companies: Alfa, Bravo and Charlie. The area of a box is proportional to the revenue from the corresponding product, while its centre represents the Product popularity and Market potential scores of the product (out of 20). The shadings of some of the boxes have got erased.
The companies classified their products into four categories based on a combination of scores (out of 20) on the two parameters - Product popularity and Market potential as given below:
The following facts are known:
1. Alfa and Bravo had the same number of products in the Blockbuster category.
2. Charlie had more products than Bravo but fewer products than Alfa in the No-hope category.
3. Each company had an equal number of products in the Promising category.
4. Charlie did not have any product in the Doubtful category, while Alfa had one product more than Bravo in this category.
5. Bravo had a higher revenue than Alfa from products in the Doubtful category.
6. Charlie had a higher revenue than Bravo from products in the Blockbuster category.
7. Bravo and Charlie had the same revenue from products in the No-hope category.
8. Alfa and Charlie had the same total revenue considering all products.
Comprehension
Each of the 23 boxes in the picture below represents a product manufactured by one of the following three companies: Alfa, Bravo and Charlie. The area of a box is proportional to the revenue from the corresponding product, while its centre represents the Product popularity and Market potential scores of the product (out of 20). The shadings of some of the boxes have got erased.
The companies classified their products into four categories based on a combination of scores (out of 20) on the two parameters - Product popularity and Market potential as given below:
The following facts are known:
1. Alfa and Bravo had the same number of products in the Blockbuster category.
2. Charlie had more products than Bravo but fewer products than Alfa in the No-hope category.
3. Each company had an equal number of products in the Promising category.
4. Charlie did not have any product in the Doubtful category, while Alfa had one product more than Bravo in this category.
5. Bravo had a higher revenue than Alfa from products in the Doubtful category.
6. Charlie had a higher revenue than Bravo from products in the Blockbuster category.
7. Bravo and Charlie had the same revenue from products in the No-hope category.
8. Alfa and Charlie had the same total revenue considering all products.
Comprehension
The base exchange rate of a currency X with respect to a currency Y is the number of units of currency Y which is equivalent in value to one unit of currency X. Currency exchange outlets buy currency at buying exchange rates that are lower than base exchange rates, and sell currency at selling exchange rates that are higher than base exchange rates.
A currency exchange outlet uses the local currency L to buy and sell three international currencies A, B, and C, but does not exchange one international currency directly with another. The base exchange rates of A, B and C with respect to L are in the ratio 100:120:1. The buying exchange rates of each of A, B, and C with respect to L are 5% below the corresponding base exchange rates, and their selling exchange rates are 10% above their corresponding base exchange rates.
The following facts are known about the outlet on a particular day:
1. The amount of L used by the outlet to buy C equals the amount of L it received by selling C.
2. The amounts of L used by the outlet to buy A and B are in the ratio 5:3.
3. The amounts of L the outlet received from the sales of A and B are in the ratio 5:9.
4. The outlet received 88000 units of L by selling A during the day.
5. The outlet started the day with some amount of L, 2500 units of A, 4800 units of B, and 48000 units of C.
6. The outlet ended the day with some amount of L, 3300 units of A, 4800 units of B,and 51000 units of C.
1200
Comprehension
The base exchange rate of a currency X with respect to a currency Y is the number of units of currency Y which is equivalent in value to one unit of currency X. Currency exchange outlets buy currency at buying exchange rates that are lower than base exchange rates, and sell currency at selling exchange rates that are higher than base exchange rates.
A currency exchange outlet uses the local currency L to buy and sell three international currencies A, B, and C, but does not exchange one international currency directly with another. The base exchange rates of A, B and C with respect to L are in the ratio 100:120:1. The buying exchange rates of each of A, B, and C with respect to L are 5% below the corresponding base exchange rates, and their selling exchange rates are 10% above their corresponding base exchange rates.
The following facts are known about the outlet on a particular day:
1. The amount of L used by the outlet to buy C equals the amount of L it received by selling C.
2. The amounts of L used by the outlet to buy A and B are in the ratio 5:3.
3. The amounts of L the outlet received from the sales of A and B are in the ratio 5:9.
4. The outlet received 88000 units of L by selling A during the day.
5. The outlet started the day with some amount of L, 2500 units of A, 4800 units of B, and 48000 units of C.
6. The outlet ended the day with some amount of L, 3300 units of A, 4800 units of B,and 51000 units of C.
Comprehension
The base exchange rate of a currency X with respect to a currency Y is the number of units of currency Y which is equivalent in value to one unit of currency X. Currency exchange outlets buy currency at buying exchange rates that are lower than base exchange rates, and sell currency at selling exchange rates that are higher than base exchange rates.
A currency exchange outlet uses the local currency L to buy and sell three international currencies A, B, and C, but does not exchange one international currency directly with another. The base exchange rates of A, B and C with respect to L are in the ratio 100:120:1. The buying exchange rates of each of A, B, and C with respect to L are 5% below the corresponding base exchange rates, and their selling exchange rates are 10% above their corresponding base exchange rates.
The following facts are known about the outlet on a particular day:
1. The amount of L used by the outlet to buy C equals the amount of L it received by selling C.
2. The amounts of L used by the outlet to buy A and B are in the ratio 5:3.
3. The amounts of L the outlet received from the sales of A and B are in the ratio 5:9.
4. The outlet received 88000 units of L by selling A during the day.
5. The outlet started the day with some amount of L, 2500 units of A, 4800 units of B, and 48000 units of C.
6. The outlet ended the day with some amount of L, 3300 units of A, 4800 units of B,and 51000 units of C.
CAT/2018.2(DILR)
Question. 112
What was the base exchange rate of currency B with respect to currency L on that day?
240
Comprehension
The base exchange rate of a currency X with respect to a currency Y is the number of units of currency Y which is equivalent in value to one unit of currency X. Currency exchange outlets buy currency at buying exchange rates that are lower than base exchange rates, and sell currency at selling exchange rates that are higher than base exchange rates.
A currency exchange outlet uses the local currency L to buy and sell three international currencies A, B, and C, but does not exchange one international currency directly with another. The base exchange rates of A, B and C with respect to L are in the ratio 100:120:1. The buying exchange rates of each of A, B, and C with respect to L are 5% below the corresponding base exchange rates, and their selling exchange rates are 10% above their corresponding base exchange rates.
The following facts are known about the outlet on a particular day:
1. The amount of L used by the outlet to buy C equals the amount of L it received by selling C.
2. The amounts of L used by the outlet to buy A and B are in the ratio 5:3.
3. The amounts of L the outlet received from the sales of A and B are in the ratio 5:9.
4. The outlet received 88000 units of L by selling A during the day.
5. The outlet started the day with some amount of L, 2500 units of A, 4800 units of B, and 48000 units of C.
6. The outlet ended the day with some amount of L, 3300 units of A, 4800 units of B,and 51000 units of C.
Comprehension
A new airlines company is planning to start operations in a country. The company has identified ten different cities which they plan to connect through their network to start with. The flight duration between any pair of cities will be less than one hour. To start operations, the company has to decide on a daily schedule.
The underlying principle that they are working on is the following:
Any person staying in any of these 10 cities should be able to make a trip to any other city in the morning and should be able to return by the evening of the same day
Comprehension
A new airlines company is planning to start operations in a country. The company has identified ten different cities which they plan to connect through their network to start with. The flight duration between any pair of cities will be less than one hour. To start operations, the company has to decide on a daily schedule.
The underlying principle that they are working on is the following:
Any person staying in any of these 10 cities should be able to make a trip to any other city in the morning and should be able to return by the evening of the same day
CAT/2017.1(DILR)
Question. 115
Suppose three of the ten cities are to be developed as hubs. A hub is a city which is connected with every other city by direct flights each way, both in the morning as well as in the evening. The only direct flights which will be scheduled are originating and/or terminating in one of the hubs. Then the minimum number of direct flights that need to be scheduled so that the underlying principle of the airline to serve all the ten cities is met without visiting more than one hub during one trip is:
Comprehension
A new airlines company is planning to start operations in a country. The company has identified ten different cities which they plan to connect through their network to start with. The flight duration between any pair of cities will be less than one hour. To start operations, the company has to decide on a daily schedule.
The underlying principle that they are working on is the following:
Any person staying in any of these 10 cities should be able to make a trip to any other city in the morning and should be able to return by the evening of the same day
CAT/2017.1(DILR)
Question. 116
Suppose the 10 cities are divided into 4 distinct groups G1, G2, G3, G4 having 3, 3, 2 and 2 cities respectively and that G1 consists of cities named A, B and C. Further, suppose that direct flights are allowed only between two cities satisfying one of the following:
1. Both cities are in G1
2. Between A and any city in G2
3. Between B and any city in G3
4. Between C and any city in G4
Then the minimum number of direct flights that satisfies the underlying principle of the airline is:
40
Comprehension
A new airlines company is planning to start operations in a country. The company has identified ten different cities which they plan to connect through their network to start with. The flight duration between any pair of cities will be less than one hour. To start operations, the company has to decide on a daily schedule.
The underlying principle that they are working on is the following:
Any person staying in any of these 10 cities should be able to make a trip to any other city in the morning and should be able to return by the evening of the same day
CAT/2017.1(DILR)
Question. 117
Suppose the 10 cities are divided into 4 distinct groups G1, G2, G3, G4 having 3, 3, 2 and 2 cities respectively and that G1 consists of cities named A, B and C. Further, suppose that direct flights are allowed only between two cities satisfying one of the following:
1. Both cities are in G1
2. Between A and any city in G2
3. Between B and any city in G3
4. Between C and any city in G4
However, due to operational difficulties at A, it was later decided that the only flights that would operate at A would be those to and from B. Cities in G2 would have to be assigned to G3 or to G4.
What would be the maximum reduction in the number of direct flights as compared to the situation before the operational difficulties arose?
Comprehension
Four cars need to travel from Akala (A) to Bakala (B). Two routes are available, one via Mamur (M) and the other via Nanur (N). The roads from A to M, and from N to B, are both short and narrow. In each case, one car takes 6 minutes to cover the distance, and each additional car increases the travel time per car by 3 minutes because of congestion. (For example, if only two cars drive from A to M, each car takes 9 minutes.) On the road from A to N, one car takes 20 minutes, and each additional car increases the travel time per car by 1 minute. On the road from M to B, one car takes 20 minutes, and each additional car increases the travel time per car by 0.9 minute.
The police department orders each car to take a particular route in such a manner that it is not possible for any car to reduce its travel time by not following the order, while the other cars are following the order.
Comprehension
Four cars need to travel from Akala (A) to Bakala (B). Two routes are available, one via Mamur (M) and the other via Nanur (N). The roads from A to M, and from N to B, are both short and narrow. In each case, one car takes 6 minutes to cover the distance, and each additional car increases the travel time per car by 3 minutes because of congestion. (For example, if only two cars drive from A to M, each car takes 9 minutes.) On the road from A to N, one car takes 20 minutes, and each additional car increases the travel time per car by 1 minute. On the road from M to B, one car takes 20 minutes, and each additional car increases the travel time per car by 0.9 minute.
The police department orders each car to take a particular route in such a manner that it is not possible for any car to reduce its travel time by not following the order, while the other cars are following the order.
Comprehension
Four cars need to travel from Akala (A) to Bakala (B). Two routes are available, one via Mamur (M) and the other via Nanur (N). The roads from A to M, and from N to B, are both short and narrow. In each case, one car takes 6 minutes to cover the distance, and each additional car increases the travel time per car by 3 minutes because of congestion. (For example, if only two cars drive from A to M, each car takes 9 minutes.) On the road from A to N, one car takes 20 minutes, and each additional car increases the travel time per car by 1 minute. On the road from M to B, one car takes 20 minutes, and each additional car increases the travel time per car by 0.9 minute.
The police department orders each car to take a particular route in such a manner that it is not possible for any car to reduce its travel time by not following the order, while the other cars are following the order.
CAT/2017.1(DILR)
Question. 120
A new one-way road is built from M to N. Each car now has three possible routes to travel from A to B: A-M-B, A-N-B and A-M-N-B. On the road from M to N, one car takes 7 minutes and each additional car increases the travel time per car by 1 minute. Assume that any car taking the A-M-N-B route travels the A-M portion at the same time as other cars taking the A-M-B route, and the N-B portion at the same time as other cars taking the A-N-B route.
How many cars would the police department order to take the A-M-N-B route so that it is not possible for any car to reduce its travel time by not following the order while the other cars follow the order? (Assume that the police department would never order all the cars to take the same route.
Comprehension
Four cars need to travel from Akala (A) to Bakala (B). Two routes are available, one via Mamur (M) and the other via Nanur (N). The roads from A to M, and from N to B, are both short and narrow. In each case, one car takes 6 minutes to cover the distance, and each additional car increases the travel time per car by 3 minutes because of congestion. (For example, if only two cars drive from A to M, each car takes 9 minutes.) On the road from A to N, one car takes 20 minutes, and each additional car increases the travel time per car by 1 minute. On the road from M to B, one car takes 20 minutes, and each additional car increases the travel time per car by 0.9 minute.
The police department orders each car to take a particular route in such a manner that it is not possible for any car to reduce its travel time by not following the order, while the other cars are following the order.
CAT/2017.1(DILR)
Question. 121
A new one-way road is built from M to N. Each car now has three possible routes to travel from A to B: A-M-B, A-N-B and A-M-N-B. On the road from M to N, one car takes 7 minutes and each additional car increases the travel time per car by 1 minute. Assume that any car taking the A-M-N-B route travels the A-M portion at the same time as other cars taking the A-M-B route, and the N-B portion at the same time as other cars taking the A-N-B route.
If all the cars follow the police order, what is the minimum travel time (in minutes) from A to B? (Assume that the police department would never order all the cars to take the same route.2
Comprehension
Applicants for the doctoral programmes of Ambi Institute of Engineering (AIE) and Bambi Institute of Engineering (BIE) have to appear for a Common Entrance Test (CET). The test has three sections: Physics (P), Chemistry (C), and Maths (M). Among those appearing for CET, those at or above the 80th percentile in at least two sections, and at or above the 90th percentile overall, are selected for Advanced Entrance Test (AET) conducted by AIE. AET is used by AIE for final selection.
For the 200 candidates who are at or above the 90th percentile overall based on CET, the following are known about their performance in CET:
1.No one is below the 80th percentile in all 3 sections.
2.150 are at or above the 80th percentile in exactly two sections.
3.The number of candidates at or above the 80th percentile only in P is the same as the number of candidates at or above the 80th percentile only in C. The same is the number of candidates at or above the 80th percentile only in M.
4.Number of candidates below 80th percentile in P: Number of candidates below 80th percentile in C: Number of candidates below 80th percentile in M = 4:2:1.
BIE uses a different process for selection. If any candidate is appearing in the AET by AIE, BIE considers their AET score for final selection provided the candidate is at or above the 80th percentile in P. Any other candidate at or above the 80th percentile in P in CET, but who is not eligible for the AET, is required to appear in a separate test to be conducted by BIE for being considered for final selection. Altogether, there are 400 candidates this year who are at or above the 80th percentile in P.
Comprehension
Applicants for the doctoral programmes of Ambi Institute of Engineering (AIE) and Bambi Institute of Engineering (BIE) have to appear for a Common Entrance Test (CET). The test has three sections: Physics (P), Chemistry (C), and Maths (M). Among those appearing for CET, those at or above the 80th percentile in at least two sections, and at or above the 90th percentile overall, are selected for Advanced Entrance Test (AET) conducted by AIE. AET is used by AIE for final selection.
For the 200 candidates who are at or above the 90th percentile overall based on CET, the following are known about their performance in CET:
1.No one is below the 80th percentile in all 3 sections.
2.150 are at or above the 80th percentile in exactly two sections.
3.The number of candidates at or above the 80th percentile only in P is the same as the number of candidates at or above the 80th percentile only in C. The same is the number of candidates at or above the 80th percentile only in M.
4.Number of candidates below 80th percentile in P: Number of candidates below 80th percentile in C: Number of candidates below 80th percentile in M = 4:2:1.
BIE uses a different process for selection. If any candidate is appearing in the AET by AIE, BIE considers their AET score for final selection provided the candidate is at or above the 80th percentile in P. Any other candidate at or above the 80th percentile in P in CET, but who is not eligible for the AET, is required to appear in a separate test to be conducted by BIE for being considered for final selection. Altogether, there are 400 candidates this year who are at or above the 80th percentile in P.
CAT/2017.1(DILR)
Question. 123
If the number of candidates who are at or above the 90th percentile overall and also at or above the 80th percentile in all three sections in CET is actually a multiple of 5, what is the number of candidates who are at or above the 90th percentile overall and at or above the 80th percentile in both P and M in CET?
60
Comprehension
Applicants for the doctoral programmes of Ambi Institute of Engineering (AIE) and Bambi Institute of Engineering (BIE) have to appear for a Common Entrance Test (CET). The test has three sections: Physics (P), Chemistry (C), and Maths (M). Among those appearing for CET, those at or above the 80th percentile in at least two sections, and at or above the 90th percentile overall, are selected for Advanced Entrance Test (AET) conducted by AIE. AET is used by AIE for final selection.
For the 200 candidates who are at or above the 90th percentile overall based on CET, the following are known about their performance in CET:
1.No one is below the 80th percentile in all 3 sections.
2.150 are at or above the 80th percentile in exactly two sections.
3.The number of candidates at or above the 80th percentile only in P is the same as the number of candidates at or above the 80th percentile only in C. The same is the number of candidates at or above the 80th percentile only in M.
4.Number of candidates below 80th percentile in P: Number of candidates below 80th percentile in C: Number of candidates below 80th percentile in M = 4:2:1.
BIE uses a different process for selection. If any candidate is appearing in the AET by AIE, BIE considers their AET score for final selection provided the candidate is at or above the 80th percentile in P. Any other candidate at or above the 80th percentile in P in CET, but who is not eligible for the AET, is required to appear in a separate test to be conducted by BIE for being considered for final selection. Altogether, there are 400 candidates this year who are at or above the 80th percentile in P.
CAT/2017.1(DILR)
Question. 124
If the number of candidates who are at or above the 90th percentile overall and also at or above the 80th percentile in all three sections in CET is actually a multiple of 5, then how many candidates were shortlisted for the AET for AIE?
170
Comprehension
Applicants for the doctoral programmes of Ambi Institute of Engineering (AIE) and Bambi Institute of Engineering (BIE) have to appear for a Common Entrance Test (CET). The test has three sections: Physics (P), Chemistry (C), and Maths (M). Among those appearing for CET, those at or above the 80th percentile in at least two sections, and at or above the 90th percentile overall, are selected for Advanced Entrance Test (AET) conducted by AIE. AET is used by AIE for final selection.
For the 200 candidates who are at or above the 90th percentile overall based on CET, the following are known about their performance in CET:
1.No one is below the 80th percentile in all 3 sections.
2.150 are at or above the 80th percentile in exactly two sections.
3.The number of candidates at or above the 80th percentile only in P is the same as the number of candidates at or above the 80th percentile only in C. The same is the number of candidates at or above the 80th percentile only in M.
4.Number of candidates below 80th percentile in P: Number of candidates below 80th percentile in C: Number of candidates below 80th percentile in M = 4:2:1.
BIE uses a different process for selection. If any candidate is appearing in the AET by AIE, BIE considers their AET score for final selection provided the candidate is at or above the 80th percentile in P. Any other candidate at or above the 80th percentile in P in CET, but who is not eligible for the AET, is required to appear in a separate test to be conducted by BIE for being considered for final selection. Altogether, there are 400 candidates this year who are at or above the 80th percentile in P.
Comprehension
An old woman had the following assets:
(a) Rs. 70 lakh in bank deposits
(b) 1 house worth Rs. 50 lakh
(c) 3 flats, each worth Rs. 30 lakh
(d) Certain number of gold coins , each worth Rs. 1 lakh
She wanted to distribute her assets among her three children; Neeta, Seeta and Geeta. The house, any of the flats or any of the coins were not to be split. That is, the house went entirely to one child; a flat went to one child and similarly, a gold coin went to one child.
Among the three, Neeta received the least amount in bank deposits, while Geeta received the highest. The value of the assets was distributed equally among the children, as were the gold coins.
Comprehension
An old woman had the following assets:
(a) Rs. 70 lakh in bank deposits
(b) 1 house worth Rs. 50 lakh
(c) 3 flats, each worth Rs. 30 lakh
(d) Certain number of gold coins , each worth Rs. 1 lakh
She wanted to distribute her assets among her three children; Neeta, Seeta and Geeta. The house, any of the flats or any of the coins were not to be split. That is, the house went entirely to one child; a flat went to one child and similarly, a gold coin went to one child.
Among the three, Neeta received the least amount in bank deposits, while Geeta received the highest. The value of the assets was distributed equally among the children, as were the gold coins.
Comprehension
An old woman had the following assets:
(a) Rs. 70 lakh in bank deposits
(b) 1 house worth Rs. 50 lakh
(c) 3 flats, each worth Rs. 30 lakh
(d) Certain number of gold coins , each worth Rs. 1 lakh
She wanted to distribute her assets among her three children; Neeta, Seeta and Geeta. The house, any of the flats or any of the coins were not to be split. That is, the house went entirely to one child; a flat went to one child and similarly, a gold coin went to one child.
Among the three, Neeta received the least amount in bank deposits, while Geeta received the highest. The value of the assets was distributed equally among the children, as were the gold coins.
CAT/2017.2(DILR)
Question. 128
The value of the assets distributed among Neeta, Seeta and Geeta was in the ratio of 1:2:3, while the gold coins were distributed among them in the ratio of 2:3:4. One child got all three flats and she did not get the house. One child, other than Geeta, got Rs. 30 lakh in bank deposits. How many gold coins did the old woman have?
Comprehension
An old woman had the following assets:
(a) Rs. 70 lakh in bank deposits
(b) 1 house worth Rs. 50 lakh
(c) 3 flats, each worth Rs. 30 lakh
(d) Certain number of gold coins , each worth Rs. 1 lakh
She wanted to distribute her assets among her three children; Neeta, Seeta and Geeta. The house, any of the flats or any of the coins were not to be split. That is, the house went entirely to one child; a flat went to one child and similarly, a gold coin went to one child.
Among the three, Neeta received the least amount in bank deposits, while Geeta received the highest. The value of the assets was distributed equally among the children, as were the gold coins.
CAT/2017.2(DILR)
Question. 129
The value of the assets distributed among Neeta, Seeta and Geeta was in the ratio of 1:2:3, while the gold coins were distributed among them in the ratio of 2:3:4. One child got all three flats and she did not get the house. One child, other than Geeta, got Rs. 30 lakh in bank deposits. how much did Seeta get in bank deposits (in lakhs of rupees)?
20
Comprehension
In an 8 X 8 chessboard a queen placed anywhere can attack another piece if the piece is present in the same row, or in the same column or in any diagonal position in any possible 4 directions, provided there is no other piece in between in the path from the queen to that piece. The columns are labelled a to h (left to right) and the rows are numbered 1 to 8 (bottom to top). The position of a piece is given by the combination of column and row labels. For example, position c5 means that the piece is in cth column and 5th row.
Comprehension
In an 8 X 8 chessboard a queen placed anywhere can attack another piece if the piece is present in the same row, or in the same column or in any diagonal position in any possible 4 directions, provided there is no other piece in between in the path from the queen to that piece. The columns are labelled a to h (left to right) and the rows are numbered 1 to 8 (bottom to top). The position of a piece is given by the combination of column and row labels. For example, position c5 means that the piece is in cth column and 5th row.
Comprehension
In an 8 X 8 chessboard a queen placed anywhere can attack another piece if the piece is present in the same row, or in the same column or in any diagonal position in any possible 4 directions, provided there is no other piece in between in the path from the queen to that piece. The columns are labelled a to h (left to right) and the rows are numbered 1 to 8 (bottom to top). The position of a piece is given by the combination of column and row labels. For example, position c5 means that the piece is in cth column and 5th row.
Comprehension
In an 8 X 8 chessboard a queen placed anywhere can attack another piece if the piece is present in the same row, or in the same column or in any diagonal position in any possible 4 directions, provided there is no other piece in between in the path from the queen to that piece. The columns are labelled a to h (left to right) and the rows are numbered 1 to 8 (bottom to top). The position of a piece is given by the combination of column and row labels. For example, position c5 means that the piece is in cth column and 5th row.
Comprehension
Eight friends: Ajit, Byomkesh, Gargi, Jayanta, Kikira, Manik, Prodosh and Tapesh are going to Delhi from Kolkata by a flight operated by Cheap Air. In the flight, sitting is arranged in 30 rows, numbered 1 to 30, each consisting of 6 seats, marked by letters A to F from left to right, respectively. Seats A to C are to the left of the aisle (the passage running from the front of the aircraft to the back), and seats D to F are to the right of the aisle. Seats A and F are by the windows and referred to as Window seats, C and D are by the aisle and are referred to as Aisle seats while B and E are referred to as Middle seats. Seats marked by consecutive letters are called consecutive seats (or seats next to each other). A seat number is a combination of the row number, followed by the letter indicating the position in the row; e.g., 1A is the left window seat in the first row, while 12E is the right middle seat in the 12th row.
Cheap Air charges Rs. 1000 extra for any seats in Rows 1, 12 and 13 as those have extra legroom. For Rows 2-10, it charges Rs. 300 extra for Window seats and Rs. 500 extra for Aisle seats. For Rows 11 and 14 to 20, it charges Rs. 200 extra for Window seats and Rs. 400 extra for Aisle seats. All other seats are available at no extra charge.
The following are known:
1. The eight friends were seated in six different rows.
2. They occupied 3 Window seats, 4 Aisle seats and 1 Middle seat.
3. Seven of them had to pay extra amounts, totaling to Rs. 4600, for their choices of seat. One of them did not pay any additional amount for his/her choice of seat.
4. Jayanta, Ajit and Byomkesh were sitting in seats marked by the same letter, in consecutive rows in increasing order of row numbers; but all of them paid different amounts for their choices of seat. One of these amounts may be zero.
5. Gargi was sitting next to Kikira, and Manik was sitting next to Jayanta.
6. Prodosh and Tapesh were sitting in seats marked by the same letter, in consecutive rows in increasing order of row numbers; but they paid different amounts for their choices of seat. One of these amounts may be zero
Comprehension
Eight friends: Ajit, Byomkesh, Gargi, Jayanta, Kikira, Manik, Prodosh and Tapesh are going to Delhi from Kolkata by a flight operated by Cheap Air. In the flight, sitting is arranged in 30 rows, numbered 1 to 30, each consisting of 6 seats, marked by letters A to F from left to right, respectively. Seats A to C are to the left of the aisle (the passage running from the front of the aircraft to the back), and seats D to F are to the right of the aisle. Seats A and F are by the windows and referred to as Window seats, C and D are by the aisle and are referred to as Aisle seats while B and E are referred to as Middle seats. Seats marked by consecutive letters are called consecutive seats (or seats next to each other). A seat number is a combination of the row number, followed by the letter indicating the position in the row; e.g., 1A is the left window seat in the first row, while 12E is the right middle seat in the 12th row.
Cheap Air charges Rs. 1000 extra for any seats in Rows 1, 12 and 13 as those have extra legroom. For Rows 2-10, it charges Rs. 300 extra for Window seats and Rs. 500 extra for Aisle seats. For Rows 11 and 14 to 20, it charges Rs. 200 extra for Window seats and Rs. 400 extra for Aisle seats. All other seats are available at no extra charge.
The following are known:
1. The eight friends were seated in six different rows.
2. They occupied 3 Window seats, 4 Aisle seats and 1 Middle seat.
3. Seven of them had to pay extra amounts, totaling to Rs. 4600, for their choices of seat. One of them did not pay any additional amount for his/her choice of seat.
4. Jayanta, Ajit and Byomkesh were sitting in seats marked by the same letter, in consecutive rows in increasing order of row numbers; but all of them paid different amounts for their choices of seat. One of these amounts may be zero.
5. Gargi was sitting next to Kikira, and Manik was sitting next to Jayanta.
6. Prodosh and Tapesh were sitting in seats marked by the same letter, in consecutive rows in increasing order of row numbers; but they paid different amounts for their choices of seat. One of these amounts may be zero
Comprehension
Eight friends: Ajit, Byomkesh, Gargi, Jayanta, Kikira, Manik, Prodosh and Tapesh are going to Delhi from Kolkata by a flight operated by Cheap Air. In the flight, sitting is arranged in 30 rows, numbered 1 to 30, each consisting of 6 seats, marked by letters A to F from left to right, respectively. Seats A to C are to the left of the aisle (the passage running from the front of the aircraft to the back), and seats D to F are to the right of the aisle. Seats A and F are by the windows and referred to as Window seats, C and D are by the aisle and are referred to as Aisle seats while B and E are referred to as Middle seats. Seats marked by consecutive letters are called consecutive seats (or seats next to each other). A seat number is a combination of the row number, followed by the letter indicating the position in the row; e.g., 1A is the left window seat in the first row, while 12E is the right middle seat in the 12th row.
Cheap Air charges Rs. 1000 extra for any seats in Rows 1, 12 and 13 as those have extra legroom. For Rows 2-10, it charges Rs. 300 extra for Window seats and Rs. 500 extra for Aisle seats. For Rows 11 and 14 to 20, it charges Rs. 200 extra for Window seats and Rs. 400 extra for Aisle seats. All other seats are available at no extra charge.
The following are known:
1. The eight friends were seated in six different rows.
2. They occupied 3 Window seats, 4 Aisle seats and 1 Middle seat.
3. Seven of them had to pay extra amounts, totaling to Rs. 4600, for their choices of seat. One of them did not pay any additional amount for his/her choice of seat.
4. Jayanta, Ajit and Byomkesh were sitting in seats marked by the same letter, in consecutive rows in increasing order of row numbers; but all of them paid different amounts for their choices of seat. One of these amounts may be zero.
5. Gargi was sitting next to Kikira, and Manik was sitting next to Jayanta.
6. Prodosh and Tapesh were sitting in seats marked by the same letter, in consecutive rows in increasing order of row numbers; but they paid different amounts for their choices of seat. One of these amounts may be zero
Comprehension
Eight friends: Ajit, Byomkesh, Gargi, Jayanta, Kikira, Manik, Prodosh and Tapesh are going to Delhi from Kolkata by a flight operated by Cheap Air. In the flight, sitting is arranged in 30 rows, numbered 1 to 30, each consisting of 6 seats, marked by letters A to F from left to right, respectively. Seats A to C are to the left of the aisle (the passage running from the front of the aircraft to the back), and seats D to F are to the right of the aisle. Seats A and F are by the windows and referred to as Window seats, C and D are by the aisle and are referred to as Aisle seats while B and E are referred to as Middle seats. Seats marked by consecutive letters are called consecutive seats (or seats next to each other). A seat number is a combination of the row number, followed by the letter indicating the position in the row; e.g., 1A is the left window seat in the first row, while 12E is the right middle seat in the 12th row.
Cheap Air charges Rs. 1000 extra for any seats in Rows 1, 12 and 13 as those have extra legroom. For Rows 2-10, it charges Rs. 300 extra for Window seats and Rs. 500 extra for Aisle seats. For Rows 11 and 14 to 20, it charges Rs. 200 extra for Window seats and Rs. 400 extra for Aisle seats. All other seats are available at no extra charge.
The following are known:
1. The eight friends were seated in six different rows.
2. They occupied 3 Window seats, 4 Aisle seats and 1 Middle seat.
3. Seven of them had to pay extra amounts, totaling to Rs. 4600, for their choices of seat. One of them did not pay any additional amount for his/her choice of seat.
4. Jayanta, Ajit and Byomkesh were sitting in seats marked by the same letter, in consecutive rows in increasing order of row numbers; but all of them paid different amounts for their choices of seat. One of these amounts may be zero.
5. Gargi was sitting next to Kikira, and Manik was sitting next to Jayanta.
6. Prodosh and Tapesh were sitting in seats marked by the same letter, in consecutive rows in increasing order of row numbers; but they paid different amounts for their choices of seat. One of these amounts may be zero
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
(i) There are three houses on each side of the road.
(ii) These six houses are labeled as P, Q, R, S, T and U.
(iii) The houses are of different colours, namely, Red, Blue, Green, Orange, Yellow and White.
(iv) The houses are of different heights.
(v) T, the tallest house, is exactly opposite to the Red coloured house.
(vi) The shortest house is exactly opposite to the Green coloured house.
(vii) U, the Orange coloured house, is located between P and S.
(viii) R, the Yellow coloured house, is exactly opposite to P.
(ix) Q, the Green coloured house, is exactly opposite to U.
(x) P, the White coloured house, is taller than R, but shorter than S and Q.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
(i) There are three houses on each side of the road.
(ii) These six houses are labeled as P, Q, R, S, T and U.
(iii) The houses are of different colours, namely, Red, Blue, Green, Orange, Yellow and White.
(iv) The houses are of different heights.
(v) T, the tallest house, is exactly opposite to the Red coloured house.
(vi) The shortest house is exactly opposite to the Green coloured house.
(vii) U, the Orange coloured house, is located between P and S.
(viii) R, the Yellow coloured house, is exactly opposite to P.
(ix) Q, the Green coloured house, is exactly opposite to U.
(x) P, the White coloured house, is taller than R, but shorter than S and Q.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
(i) There are three houses on each side of the road.
(ii) These six houses are labeled as P, Q, R, S, T and U.
(iii) The houses are of different colours, namely, Red, Blue, Green, Orange, Yellow and White.
(iv) The houses are of different heights.
(v) T, the tallest house, is exactly opposite to the Red coloured house.
(vi) The shortest house is exactly opposite to the Green coloured house.
(vii) U, the Orange coloured house, is located between P and S.
(viii) R, the Yellow coloured house, is exactly opposite to P.
(ix) Q, the Green coloured house, is exactly opposite to U.
(x) P, the White coloured house, is taller than R, but shorter than S and Q.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
Abdul, Bikram and Chetan are three professional traders who trade in shares of a company XYZ Ltd. Abdul follows the strategy of buying at the opening of the day at 10 am and selling the whole lot at the close of the day at 3 pm. Bikram follows the strategy of buying at hourly intervals: 10 am, 11 am, 12 noon, 1 pm and 2 pm, and selling the whole lot at the close of the day. Further, he buys an equal number of shares in each purchase. Chetan follows a similar pattern as Bikram but his strategy is somewhat different. Chetan’s total investment amount is divided equally among his purchases. The profit or loss made by each investor is the difference between the sale value at the close of the day less the investment in purchase. The “return” for each investor is defined as the ratio of the profit or loss to the investment amount expressed as a percentage.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
Abdul, Bikram and Chetan are three professional traders who trade in shares of a company XYZ Ltd. Abdul follows the strategy of buying at the opening of the day at 10 am and selling the whole lot at the close of the day at 3 pm. Bikram follows the strategy of buying at hourly intervals: 10 am, 11 am, 12 noon, 1 pm and 2 pm, and selling the whole lot at the close of the day. Further, he buys an equal number of shares in each purchase. Chetan follows a similar pattern as Bikram but his strategy is somewhat different. Chetan’s total investment amount is divided equally among his purchases. The profit or loss made by each investor is the difference between the sale value at the close of the day less the investment in purchase. The “return” for each investor is defined as the ratio of the profit or loss to the investment amount expressed as a percentage.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
Abdul, Bikram and Chetan are three professional traders who trade in shares of a company XYZ Ltd. Abdul follows the strategy of buying at the opening of the day at 10 am and selling the whole lot at the close of the day at 3 pm. Bikram follows the strategy of buying at hourly intervals: 10 am, 11 am, 12 noon, 1 pm and 2 pm, and selling the whole lot at the close of the day. Further, he buys an equal number of shares in each purchase. Chetan follows a similar pattern as Bikram but his strategy is somewhat different. Chetan’s total investment amount is divided equally among his purchases. The profit or loss made by each investor is the difference between the sale value at the close of the day less the investment in purchase. The “return” for each investor is defined as the ratio of the profit or loss to the investment amount expressed as a percentage.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
Abdul, Bikram and Chetan are three professional traders who trade in shares of a company XYZ Ltd. Abdul follows the strategy of buying at the opening of the day at 10 am and selling the whole lot at the close of the day at 3 pm. Bikram follows the strategy of buying at hourly intervals: 10 am, 11 am, 12 noon, 1 pm and 2 pm, and selling the whole lot at the close of the day. Further, he buys an equal number of shares in each purchase. Chetan follows a similar pattern as Bikram but his strategy is somewhat different. Chetan’s total investment amount is divided equally among his purchases. The profit or loss made by each investor is the difference between the sale value at the close of the day less the investment in purchase. The “return” for each investor is defined as the ratio of the profit or loss to the investment amount expressed as a percentage.
CAT/2008(DILR)
Question. 144
One day, two other traders, Dane and Emily joined Abdul, Bikram and Chetan for trading in the shares of XYZ Ltd. Dane followed a strategy of buying equal numbers of shares at 10 am, 11 am and 12 noon, and selling the same numbers at 1 pm, 2 pm and 3 pm. Emily, on the other hand, followed the strategy of buying shares using all her money at 10 am and selling all of them at 12 noon and again buying the shares for all the money at 1 pm and again selling all of them at the close of the day at 3 pm. At the close of the day the following was observed:
(i) Abdul lost money in the transactions.
(ii) Both Dane and Emily made profits.
(iii) There was an increase in share price during the closing hour compared to the price at 2 pm.
(iv) Share price at 12 noon was lower than the opening price.
Share price was at its highest at
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
Abdul, Bikram and Chetan are three professional traders who trade in shares of a company XYZ Ltd. Abdul follows the strategy of buying at the opening of the day at 10 am and selling the whole lot at the close of the day at 3 pm. Bikram follows the strategy of buying at hourly intervals: 10 am, 11 am, 12 noon, 1 pm and 2 pm, and selling the whole lot at the close of the day. Further, he buys an equal number of shares in each purchase. Chetan follows a similar pattern as Bikram but his strategy is somewhat different. Chetan’s total investment amount is divided equally among his purchases. The profit or loss made by each investor is the difference between the sale value at the close of the day less the investment in purchase. The “return” for each investor is defined as the ratio of the profit or loss to the investment amount expressed as a percentage.
CAT/2008(DILR)
Question. 145
One day, two other traders, Dane and Emily joined Abdul, Bikram and Chetan for trading in the shares of XYZ Ltd. Dane followed a strategy of buying equal numbers of shares at 10 am, 11 am and 12 noon, and selling the same numbers at 1 pm, 2 pm and 3 pm. Emily, on the other hand, followed the strategy of buying shares using all her money at 10 am and selling all of them at 12 noon and again buying the shares for all the money at 1 pm and again selling all of them at the close of the day at 3 pm. At the close of the day the following was observed:
(i) Abdul lost money in the transactions.
(ii) Both Dane and Emily made profits.
(iii) There was an increase in share price during the closing hour compared to the price at 2 pm.
(iv) Share price at 12 noon was lower than the opening price.
Which of the following is necessarily false?
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
A significant amount of traffic flows from point S to point T in the one-way street network shown below. Points A, B, C, and D are junctions in the network, and the arrows mark the direction of traffic flow. The fuel cost in rupees for travelling along a street is indicated by the number adjacent to the arrow representing the street.
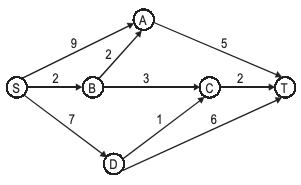
Motorists travelling from point S to point T would obviously take the route for which the total cost of travelling is the minimum. If two or more routes have the same least travel cost, then motorists are indifferent between them. Hence, the traffic gets evenly distributed among all the least cost routes.
The government can control the flow of traffic only by levying appropriate toll at each junction. For example, if a motorist takes the route S-A-T (using junction A alone), then the total cost of travel would be Rs 14 (i.e., Rs 9 + Rs 5) plus the toll charged at junction A.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
A significant amount of traffic flows from point S to point T in the one-way street network shown below. Points A, B, C, and D are junctions in the network, and the arrows mark the direction of traffic flow. The fuel cost in rupees for travelling along a street is indicated by the number adjacent to the arrow representing the street.

Motorists travelling from point S to point T would obviously take the route for which the total cost of travelling is the minimum. If two or more routes have the same least travel cost, then motorists are indifferent between them. Hence, the traffic gets evenly distributed among all the least cost routes.
The government can control the flow of traffic only by levying appropriate toll at each junction. For example, if a motorist takes the route S-A-T (using junction A alone), then the total cost of travel would be Rs 14 (i.e., Rs 9 + Rs 5) plus the toll charged at junction A.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
A significant amount of traffic flows from point S to point T in the one-way street network shown below. Points A, B, C, and D are junctions in the network, and the arrows mark the direction of traffic flow. The fuel cost in rupees for travelling along a street is indicated by the number adjacent to the arrow representing the street.

Motorists travelling from point S to point T would obviously take the route for which the total cost of travelling is the minimum. If two or more routes have the same least travel cost, then motorists are indifferent between them. Hence, the traffic gets evenly distributed among all the least cost routes.
The government can control the flow of traffic only by levying appropriate toll at each junction. For example, if a motorist takes the route S-A-T (using junction A alone), then the total cost of travel would be Rs 14 (i.e., Rs 9 + Rs 5) plus the toll charged at junction A.
CAT/2006(DILR)
Question. 148
If the government wants to ensure that all motorists travelling from S to T pay the same amount (fuel costs and toll combined) regardless of the route they choose and the street from B to C is under repairs (and hence unusable), then a feasible set of toll charged (in rupees) at junctions A, B, C, and D respectively to achieve this goal is:
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
A significant amount of traffic flows from point S to point T in the one-way street network shown below. Points A, B, C, and D are junctions in the network, and the arrows mark the direction of traffic flow. The fuel cost in rupees for travelling along a street is indicated by the number adjacent to the arrow representing the street.

Motorists travelling from point S to point T would obviously take the route for which the total cost of travelling is the minimum. If two or more routes have the same least travel cost, then motorists are indifferent between them. Hence, the traffic gets evenly distributed among all the least cost routes.
The government can control the flow of traffic only by levying appropriate toll at each junction. For example, if a motorist takes the route S-A-T (using junction A alone), then the total cost of travel would be Rs 14 (i.e., Rs 9 + Rs 5) plus the toll charged at junction A.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
A significant amount of traffic flows from point S to point T in the one-way street network shown below. Points A, B, C, and D are junctions in the network, and the arrows mark the direction of traffic flow. The fuel cost in rupees for travelling along a street is indicated by the number adjacent to the arrow representing the street.

Motorists travelling from point S to point T would obviously take the route for which the total cost of travelling is the minimum. If two or more routes have the same least travel cost, then motorists are indifferent between them. Hence, the traffic gets evenly distributed among all the least cost routes.
The government can control the flow of traffic only by levying appropriate toll at each junction. For example, if a motorist takes the route S-A-T (using junction A alone), then the total cost of travel would be Rs 14 (i.e., Rs 9 + Rs 5) plus the toll charged at junction A.
CAT/2006(DILR)
Question. 150
The government wants to devise a toll policy such that the total cost to the commuters per trip is minimized. The policy should also ensure that not more than 70 per cent of the total traffic passes through junction B. The cost incurred by the commuter travelling from point S to point T under this policy will be:
Comprehension
Directions for questions 11 to 15: Answer the questions on the basis of the information given below:
Mathematicians are assigned a number called Erdös number (named after the famous mathematician, Paul Erdös). Only Paul Erdös himself has an Erdös number of zero. Any mathematician who has written a research paper with Erdös has an Erdös number of 1. For other mathematicians, the calculation of his/ her Erdös number is illustrated below:
Suppose that a mathematician X has co-authored papers with several other mathematicians. From among them, mathematician Y has the smallest Erdös number. Let the Erdös number of Y be y. Then X has an Erdös number of y+1 . Hence any mathematician with no co-authorship chain connected to Erdös has an Erdös number of infinity.
In a seven day long mini-conference organized in memory of Paul Erdös, a close group of eight mathematicians, call them A, B, C, D, E, F, G and H, discussed some research problems. At the beginning of the conference, A was the only participant who had an infinite Erdös number. Nobody had an Erdös number less than that of F.
1. On the third day of the conference F co-authored a paper jointly with A and C. This reduced the average Erdös number of the group of eight mathematicians to 3. The Erdös numbers of B, D, E, G and H remained unchanged with the writing of this paper. Further, no other co-authorship among any three members would have reduced the average Erdös number of the group of eight to as low as 3.
2. At the end of the third day, five members of this group had identical Erdös numbers while the other three had Erdös numbers distinct from each other.
3. On the fifth day, E co-authored a paper with F which reduced the group's average Erdös number by 0.5. The Erdös numbers of the remaining six were unchanged with the writing of this paper.
4. No other paper was written during the conference
Comprehension
Directions for questions 11 to 15: Answer the questions on the basis of the information given below:
Mathematicians are assigned a number called Erdös number (named after the famous mathematician, Paul Erdös). Only Paul Erdös himself has an Erdös number of zero. Any mathematician who has written a research paper with Erdös has an Erdös number of 1. For other mathematicians, the calculation of his/ her Erdös number is illustrated below:
Suppose that a mathematician X has co-authored papers with several other mathematicians. From among them, mathematician Y has the smallest Erdös number. Let the Erdös number of Y be y. Then X has an Erdös number of y+1 . Hence any mathematician with no co-authorship chain connected to Erdös has an Erdös number of infinity.
In a seven day long mini-conference organized in memory of Paul Erdös, a close group of eight mathematicians, call them A, B, C, D, E, F, G and H, discussed some research problems. At the beginning of the conference, A was the only participant who had an infinite Erdös number. Nobody had an Erdös number less than that of F.
1. On the third day of the conference F co-authored a paper jointly with A and C. This reduced the average Erdös number of the group of eight mathematicians to 3. The Erdös numbers of B, D, E, G and H remained unchanged with the writing of this paper. Further, no other co-authorship among any three members would have reduced the average Erdös number of the group of eight to as low as 3.
2. At the end of the third day, five members of this group had identical Erdös numbers while the other three had Erdös numbers distinct from each other.
3. On the fifth day, E co-authored a paper with F which reduced the group's average Erdös number by 0.5. The Erdös numbers of the remaining six were unchanged with the writing of this paper.
4. No other paper was written during the conference
Comprehension
Directions for questions 11 to 15: Answer the questions on the basis of the information given below:
Mathematicians are assigned a number called Erdös number (named after the famous mathematician, Paul Erdös). Only Paul Erdös himself has an Erdös number of zero. Any mathematician who has written a research paper with Erdös has an Erdös number of 1. For other mathematicians, the calculation of his/ her Erdös number is illustrated below:
Suppose that a mathematician X has co-authored papers with several other mathematicians. From among them, mathematician Y has the smallest Erdös number. Let the Erdös number of Y be y. Then X has an Erdös number of y+1 . Hence any mathematician with no co-authorship chain connected to Erdös has an Erdös number of infinity.
In a seven day long mini-conference organized in memory of Paul Erdös, a close group of eight mathematicians, call them A, B, C, D, E, F, G and H, discussed some research problems. At the beginning of the conference, A was the only participant who had an infinite Erdös number. Nobody had an Erdös number less than that of F.
1. On the third day of the conference F co-authored a paper jointly with A and C. This reduced the average Erdös number of the group of eight mathematicians to 3. The Erdös numbers of B, D, E, G and H remained unchanged with the writing of this paper. Further, no other co-authorship among any three members would have reduced the average Erdös number of the group of eight to as low as 3.
2. At the end of the third day, five members of this group had identical Erdös numbers while the other three had Erdös numbers distinct from each other.
3. On the fifth day, E co-authored a paper with F which reduced the group's average Erdös number by 0.5. The Erdös numbers of the remaining six were unchanged with the writing of this paper.
4. No other paper was written during the conference
Comprehension
Directions for questions 11 to 15: Answer the questions on the basis of the information given below:
Mathematicians are assigned a number called Erdös number (named after the famous mathematician, Paul Erdös). Only Paul Erdös himself has an Erdös number of zero. Any mathematician who has written a research paper with Erdös has an Erdös number of 1. For other mathematicians, the calculation of his/ her Erdös number is illustrated below:
Suppose that a mathematician X has co-authored papers with several other mathematicians. From among them, mathematician Y has the smallest Erdös number. Let the Erdös number of Y be y. Then X has an Erdös number of y+1 . Hence any mathematician with no co-authorship chain connected to Erdös has an Erdös number of infinity.
In a seven day long mini-conference organized in memory of Paul Erdös, a close group of eight mathematicians, call them A, B, C, D, E, F, G and H, discussed some research problems. At the beginning of the conference, A was the only participant who had an infinite Erdös number. Nobody had an Erdös number less than that of F.
1. On the third day of the conference F co-authored a paper jointly with A and C. This reduced the average Erdös number of the group of eight mathematicians to 3. The Erdös numbers of B, D, E, G and H remained unchanged with the writing of this paper. Further, no other co-authorship among any three members would have reduced the average Erdös number of the group of eight to as low as 3.
2. At the end of the third day, five members of this group had identical Erdös numbers while the other three had Erdös numbers distinct from each other.
3. On the fifth day, E co-authored a paper with F which reduced the group's average Erdös number by 0.5. The Erdös numbers of the remaining six were unchanged with the writing of this paper.
4. No other paper was written during the conference
Comprehension
Directions for questions 11 to 15: Answer the questions on the basis of the information given below:
Mathematicians are assigned a number called Erdös number (named after the famous mathematician, Paul Erdös). Only Paul Erdös himself has an Erdös number of zero. Any mathematician who has written a research paper with Erdös has an Erdös number of 1. For other mathematicians, the calculation of his/ her Erdös number is illustrated below:
Suppose that a mathematician X has co-authored papers with several other mathematicians. From among them, mathematician Y has the smallest Erdös number. Let the Erdös number of Y be y. Then X has an Erdös number of y+1 . Hence any mathematician with no co-authorship chain connected to Erdös has an Erdös number of infinity.
In a seven day long mini-conference organized in memory of Paul Erdös, a close group of eight mathematicians, call them A, B, C, D, E, F, G and H, discussed some research problems. At the beginning of the conference, A was the only participant who had an infinite Erdös number. Nobody had an Erdös number less than that of F.
1. On the third day of the conference F co-authored a paper jointly with A and C. This reduced the average Erdös number of the group of eight mathematicians to 3. The Erdös numbers of B, D, E, G and H remained unchanged with the writing of this paper. Further, no other co-authorship among any three members would have reduced the average Erdös number of the group of eight to as low as 3.
2. At the end of the third day, five members of this group had identical Erdös numbers while the other three had Erdös numbers distinct from each other.
3. On the fifth day, E co-authored a paper with F which reduced the group's average Erdös number by 0.5. The Erdös numbers of the remaining six were unchanged with the writing of this paper.
4. No other paper was written during the conference
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
K, L, M, N, P, Q, R, S, U and W are the only ten members in a department. There is a proposal to form a team from within the members of the department, subject to the following conditions :
1. A team must include exactly one among P, R and S.
2. A team must include either M or Q, but not both.
3. If a team includes K, then it must also include L, and vice versa.
4. If a team includes one among S, U and W, then it must also include the other two.
5. L and N cannot be members of the same team.
6. L and U cannot be members of the same team.
The size of a team is defined as the number of members in the team.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
K, L, M, N, P, Q, R, S, U and W are the only ten members in a department. There is a proposal to form a team from within the members of the department, subject to the following conditions :
1. A team must include exactly one among P, R and S.
2. A team must include either M or Q, but not both.
3. If a team includes K, then it must also include L, and vice versa.
4. If a team includes one among S, U and W, then it must also include the other two.
5. L and N cannot be members of the same team.
6. L and U cannot be members of the same team.
The size of a team is defined as the number of members in the team.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
K, L, M, N, P, Q, R, S, U and W are the only ten members in a department. There is a proposal to form a team from within the members of the department, subject to the following conditions :
1. A team must include exactly one among P, R and S.
2. A team must include either M or Q, but not both.
3. If a team includes K, then it must also include L, and vice versa.
4. If a team includes one among S, U and W, then it must also include the other two.
5. L and N cannot be members of the same team.
6. L and U cannot be members of the same team.
The size of a team is defined as the number of members in the team.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
K, L, M, N, P, Q, R, S, U and W are the only ten members in a department. There is a proposal to form a team from within the members of the department, subject to the following conditions :
1. A team must include exactly one among P, R and S.
2. A team must include either M or Q, but not both.
3. If a team includes K, then it must also include L, and vice versa.
4. If a team includes one among S, U and W, then it must also include the other two.
5. L and N cannot be members of the same team.
6. L and U cannot be members of the same team.
The size of a team is defined as the number of members in the team.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
K, L, M, N, P, Q, R, S, U and W are the only ten members in a department. There is a proposal to form a team from within the members of the department, subject to the following conditions :
1. A team must include exactly one among P, R and S.
2. A team must include either M or Q, but not both.
3. If a team includes K, then it must also include L, and vice versa.
4. If a team includes one among S, U and W, then it must also include the other two.
5. L and N cannot be members of the same team.
6. L and U cannot be members of the same team.
The size of a team is defined as the number of members in the team.
Comprehension
Directions for questions 16 to 20: Answer the questions on the basis of the information given below:
Two traders, Chetan and Michael, were involved in the buying and selling of MCS shares over five trading days. At the beginning of the first day, the MCS share was priced at Rs 100, while at the end of the fifth day it was priced at Rs 110. At the end of each day, the MCS share price either went up by Rs 10, or else, it came down by Rs 10. Both Chetan and Michael took buying and selling decisions at the end of each trading day. The beginning price of MCS share on a given day was the same as the ending price of the previous day. Chetan and Michael started with the same number of shares and amount of cash, and had enough of both. Below are some additional facts about how Chetan and Michael traded over the five trading days.
1. Each day if the price went up, Chetan sold 10 shares of MCS at the closing price. On the other hand, each day if the price went down, he bought 10 shares at the closing price.
2. If on any day, the closing price was above Rs 110, then Michael sold 10 shares of MCS, while if it was below Rs 90, he bought 10 shares, all at the closing price.
Comprehension
Directions for questions 16 to 20: Answer the questions on the basis of the information given below:
Two traders, Chetan and Michael, were involved in the buying and selling of MCS shares over five trading days. At the beginning of the first day, the MCS share was priced at Rs 100, while at the end of the fifth day it was priced at Rs 110. At the end of each day, the MCS share price either went up by Rs 10, or else, it came down by Rs 10. Both Chetan and Michael took buying and selling decisions at the end of each trading day. The beginning price of MCS share on a given day was the same as the ending price of the previous day. Chetan and Michael started with the same number of shares and amount of cash, and had enough of both. Below are some additional facts about how Chetan and Michael traded over the five trading days.
1. Each day if the price went up, Chetan sold 10 shares of MCS at the closing price. On the other hand, each day if the price went down, he bought 10 shares at the closing price.
2. If on any day, the closing price was above Rs 110, then Michael sold 10 shares of MCS, while if it was below Rs 90, he bought 10 shares, all at the closing price.
Comprehension
Directions for questions 16 to 20: Answer the questions on the basis of the information given below:
Two traders, Chetan and Michael, were involved in the buying and selling of MCS shares over five trading days. At the beginning of the first day, the MCS share was priced at Rs 100, while at the end of the fifth day it was priced at Rs 110. At the end of each day, the MCS share price either went up by Rs 10, or else, it came down by Rs 10. Both Chetan and Michael took buying and selling decisions at the end of each trading day. The beginning price of MCS share on a given day was the same as the ending price of the previous day. Chetan and Michael started with the same number of shares and amount of cash, and had enough of both. Below are some additional facts about how Chetan and Michael traded over the five trading days.
1. Each day if the price went up, Chetan sold 10 shares of MCS at the closing price. On the other hand, each day if the price went down, he bought 10 shares at the closing price.
2. If on any day, the closing price was above Rs 110, then Michael sold 10 shares of MCS, while if it was below Rs 90, he bought 10 shares, all at the closing price.
Comprehension
Directions for questions 16 to 20: Answer the questions on the basis of the information given below:
Two traders, Chetan and Michael, were involved in the buying and selling of MCS shares over five trading days. At the beginning of the first day, the MCS share was priced at Rs 100, while at the end of the fifth day it was priced at Rs 110. At the end of each day, the MCS share price either went up by Rs 10, or else, it came down by Rs 10. Both Chetan and Michael took buying and selling decisions at the end of each trading day. The beginning price of MCS share on a given day was the same as the ending price of the previous day. Chetan and Michael started with the same number of shares and amount of cash, and had enough of both. Below are some additional facts about how Chetan and Michael traded over the five trading days.
1. Each day if the price went up, Chetan sold 10 shares of MCS at the closing price. On the other hand, each day if the price went down, he bought 10 shares at the closing price.
2. If on any day, the closing price was above Rs 110, then Michael sold 10 shares of MCS, while if it was below Rs 90, he bought 10 shares, all at the closing price.
Comprehension
Directions for questions 16 to 20: Answer the questions on the basis of the information given below:
Two traders, Chetan and Michael, were involved in the buying and selling of MCS shares over five trading days. At the beginning of the first day, the MCS share was priced at Rs 100, while at the end of the fifth day it was priced at Rs 110. At the end of each day, the MCS share price either went up by Rs 10, or else, it came down by Rs 10. Both Chetan and Michael took buying and selling decisions at the end of each trading day. The beginning price of MCS share on a given day was the same as the ending price of the previous day. Chetan and Michael started with the same number of shares and amount of cash, and had enough of both. Below are some additional facts about how Chetan and Michael traded over the five trading days.
1. Each day if the price went up, Chetan sold 10 shares of MCS at the closing price. On the other hand, each day if the price went down, he bought 10 shares at the closing price.
2. If on any day, the closing price was above Rs 110, then Michael sold 10 shares of MCS, while if it was below Rs 90, he bought 10 shares, all at the closing price.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below
Venkat, a stockbroker, invested a part of his money in the stock of four companies — A, B, C and D. Each of these companies belonged to different industries, viz., Cement, Information Technology (IT), Auto, and Steel, in no particular order. At the-time of investment, the price of each stock was Rs l00. Venkat purchased only one stock of each of these companies. He was expecting returns of 20%, 10%, 30% and 40% from the stock of companies A, B, C and D, respectively. Returns are defined as the change in the value of the stock after one year, expressed as a percentage of the initial value. During the year, two of these companies announced extraordinarily good results. One of these two companies belonged to the Cement or the IT industry, while the other one belonged to either the Steel or the Auto industry. As a result, the returns on the stocks of these two companies were higher than the initially expected returns. For the company belonging to the Cement or the IT industry with extraordinarily good results, the returns were twice that of the initially expected returns. For the company belonging to the Steel or[ the Auto industry, the returns on announcement of extraordinarily good results were only one and a half times that of the initially expected returns. For the remaining two companies.
Which do not announce extraordinarily good results, the returns realized during the year were the same as initially expected.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below
Venkat, a stockbroker, invested a part of his money in the stock of four companies — A, B, C and D. Each of these companies belonged to different industries, viz., Cement, Information Technology (IT), Auto, and Steel, in no particular order. At the-time of investment, the price of each stock was Rs l00. Venkat purchased only one stock of each of these companies. He was expecting returns of 20%, 10%, 30% and 40% from the stock of companies A, B, C and D, respectively. Returns are defined as the change in the value of the stock after one year, expressed as a percentage of the initial value. During the year, two of these companies announced extraordinarily good results. One of these two companies belonged to the Cement or the IT industry, while the other one belonged to either the Steel or the Auto industry. As a result, the returns on the stocks of these two companies were higher than the initially expected returns. For the company belonging to the Cement or the IT industry with extraordinarily good results, the returns were twice that of the initially expected returns. For the company belonging to the Steel or[ the Auto industry, the returns on announcement of extraordinarily good results were only one and a half times that of the initially expected returns. For the remaining two companies.
Which do not announce extraordinarily good results, the returns realized during the year were the same as initially expected.
CAT/2005(DILR)
Question. 167
If Venkat earned a 35% return on average during the year, then which of these statements would necessarily be true?
I. Company A belonged either to Auto or to Steel Industry.
II. Company B did not announce extraordinarily good results.
III. Company A announced extraordinarily good results.
IV. Company D did not announce extraordinarily good results
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below
Venkat, a stockbroker, invested a part of his money in the stock of four companies — A, B, C and D. Each of these companies belonged to different industries, viz., Cement, Information Technology (IT), Auto, and Steel, in no particular order. At the-time of investment, the price of each stock was Rs l00. Venkat purchased only one stock of each of these companies. He was expecting returns of 20%, 10%, 30% and 40% from the stock of companies A, B, C and D, respectively. Returns are defined as the change in the value of the stock after one year, expressed as a percentage of the initial value. During the year, two of these companies announced extraordinarily good results. One of these two companies belonged to the Cement or the IT industry, while the other one belonged to either the Steel or the Auto industry. As a result, the returns on the stocks of these two companies were higher than the initially expected returns. For the company belonging to the Cement or the IT industry with extraordinarily good results, the returns were twice that of the initially expected returns. For the company belonging to the Steel or[ the Auto industry, the returns on announcement of extraordinarily good results were only one and a half times that of the initially expected returns. For the remaining two companies.
Which do not announce extraordinarily good results, the returns realized during the year were the same as initially expected.
CAT/2005(DILR)
Question. 168
If Venkat earned a 38.75% return on average during the year, then which of these statement(s) would necessarily be true?
I. Company C belonged either to Auto or to Steel Industry.
II. Company D belonged either to Auto or to Steel Industry.
III. Company A announced extraordinarily good results.
IV. Company B did not announce extraordinarily good results.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below
Venkat, a stockbroker, invested a part of his money in the stock of four companies — A, B, C and D. Each of these companies belonged to different industries, viz., Cement, Information Technology (IT), Auto, and Steel, in no particular order. At the-time of investment, the price of each stock was Rs l00. Venkat purchased only one stock of each of these companies. He was expecting returns of 20%, 10%, 30% and 40% from the stock of companies A, B, C and D, respectively. Returns are defined as the change in the value of the stock after one year, expressed as a percentage of the initial value. During the year, two of these companies announced extraordinarily good results. One of these two companies belonged to the Cement or the IT industry, while the other one belonged to either the Steel or the Auto industry. As a result, the returns on the stocks of these two companies were higher than the initially expected returns. For the company belonging to the Cement or the IT industry with extraordinarily good results, the returns were twice that of the initially expected returns. For the company belonging to the Steel or[ the Auto industry, the returns on announcement of extraordinarily good results were only one and a half times that of the initially expected returns. For the remaining two companies.
Which do not announce extraordinarily good results, the returns realized during the year were the same as initially expected.
CAT/2005(DILR)
Question. 169
If Company C belonged to the Cement or the IT industry and did announce extraordinarily good results, then which of these statement(s) would necessarily be true?
I. Venkat earned not more than 36.25% return on average.
II. Venkat earned not less than 33.75% return on average.
III. If Venkat earned 33.75% return on average, Company A announced extraordinarily good results.
IV. If Venkat earned 33.75% return on average, Company B belonged either to Auto or to Steel Industry.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below
The table below presents the revenue (in million rupees) of four firms in three states. These firms, Honest Ltd., Aggressive Ltd., Truthful Ltd. and Profitable Ltd. are disguised in the table as A,B,C and D, in no particular order.

Further, it is known that :
• In the state of MP, Truthful Ltd. has the highest market share.
• Aggressive Ltd.’s aggregate revenue differs from Honest Ltd.’s by Rs. 5 million.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below
The table below presents the revenue (in million rupees) of four firms in three states. These firms, Honest Ltd., Aggressive Ltd., Truthful Ltd. and Profitable Ltd. are disguised in the table as A,B,C and D, in no particular order.

Further, it is known that :
• In the state of MP, Truthful Ltd. has the highest market share.
• Aggressive Ltd.’s aggregate revenue differs from Honest Ltd.’s by Rs. 5 million.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below
The table below presents the revenue (in million rupees) of four firms in three states. These firms, Honest Ltd., Aggressive Ltd., Truthful Ltd. and Profitable Ltd. are disguised in the table as A,B,C and D, in no particular order.

Further, it is known that :
• In the state of MP, Truthful Ltd. has the highest market share.
• Aggressive Ltd.’s aggregate revenue differs from Honest Ltd.’s by Rs. 5 million.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below
The table below presents the revenue (in million rupees) of four firms in three states. These firms, Honest Ltd., Aggressive Ltd., Truthful Ltd. and Profitable Ltd. are disguised in the table as A,B,C and D, in no particular order.

Further, it is known that :
• In the state of MP, Truthful Ltd. has the highest market share.
• Aggressive Ltd.’s aggregate revenue differs from Honest Ltd.’s by Rs. 5 million.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
In the table below is the listing of players, seeded from highest (#1) to lowest (#32), who are due to play in an Association of Tennis Players (ATP) tournament for women. This tournament has four knockout rounds before the final, i.e., first round, second round, quarterfinals, and semi-finals. In the first round, the highest seeded player plays the lowest seeded player (seed # 32) which is designated match No.1 of first round; the 2nd seeded player plays the 31 st seeded player which is designated match No.2 of the first round, and so on. Thus, for instance, match No. 16 of first round is to be played between 16th seeded player and the 17th seeded player. In the second round, the winner of match No.1 of first round plays the winner of match No. 16 of first round and is designated match No.1 of second round. Similarly, the winner of match No.2 of first round plays the winner of match No. 15 of first round, and is designated match No.2 of second round. Thus, for instance, match No.8 of the second round is to be played between the winner of match No.8 of first round and the winner of match No.9 of first round. The same pattern is followed for later rounds as well.

Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
In the table below is the listing of players, seeded from highest (#1) to lowest (#32), who are due to play in an Association of Tennis Players (ATP) tournament for women. This tournament has four knockout rounds before the final, i.e., first round, second round, quarterfinals, and semi-finals. In the first round, the highest seeded player plays the lowest seeded player (seed # 32) which is designated match No.1 of first round; the 2nd seeded player plays the 31 st seeded player which is designated match No.2 of the first round, and so on. Thus, for instance, match No. 16 of first round is to be played between 16th seeded player and the 17th seeded player. In the second round, the winner of match No.1 of first round plays the winner of match No. 16 of first round and is designated match No.1 of second round. Similarly, the winner of match No.2 of first round plays the winner of match No. 15 of first round, and is designated match No.2 of second round. Thus, for instance, match No.8 of the second round is to be played between the winner of match No.8 of first round and the winner of match No.9 of first round. The same pattern is followed for later rounds as well.

Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
In the table below is the listing of players, seeded from highest (#1) to lowest (#32), who are due to play in an Association of Tennis Players (ATP) tournament for women. This tournament has four knockout rounds before the final, i.e., first round, second round, quarterfinals, and semi-finals. In the first round, the highest seeded player plays the lowest seeded player (seed # 32) which is designated match No.1 of first round; the 2nd seeded player plays the 31 st seeded player which is designated match No.2 of the first round, and so on. Thus, for instance, match No. 16 of first round is to be played between 16th seeded player and the 17th seeded player. In the second round, the winner of match No.1 of first round plays the winner of match No. 16 of first round and is designated match No.1 of second round. Similarly, the winner of match No.2 of first round plays the winner of match No. 15 of first round, and is designated match No.2 of second round. Thus, for instance, match No.8 of the second round is to be played between the winner of match No.8 of first round and the winner of match No.9 of first round. The same pattern is followed for later rounds as well.

Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
In the table below is the listing of players, seeded from highest (#1) to lowest (#32), who are due to play in an Association of Tennis Players (ATP) tournament for women. This tournament has four knockout rounds before the final, i.e., first round, second round, quarterfinals, and semi-finals. In the first round, the highest seeded player plays the lowest seeded player (seed # 32) which is designated match No.1 of first round; the 2nd seeded player plays the 31 st seeded player which is designated match No.2 of the first round, and so on. Thus, for instance, match No. 16 of first round is to be played between 16th seeded player and the 17th seeded player. In the second round, the winner of match No.1 of first round plays the winner of match No. 16 of first round and is designated match No.1 of second round. Similarly, the winner of match No.2 of first round plays the winner of match No. 15 of first round, and is designated match No.2 of second round. Thus, for instance, match No.8 of the second round is to be played between the winner of match No.8 of first round and the winner of match No.9 of first round. The same pattern is followed for later rounds as well.

Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
Help Distress (HD) is an NGO involved in providing assistance to people suffering from natural disasters. Currently, it has 37 volunteers. They are involved in three projects: Tsunami Relief (TR) in Tamil Nadu, Flood Relief (FR) in Maharashtra, and Earthquake Relief (ER) in Gujarat. Each volunteer working with Help Distress has to be involved in at least one relief work project.
• A Maximum number of volunteers are involved in the FR project. Among them, the number of volunteers involved in FR project alone. is equal to the volunteers having additional involvement in the ER project.
• The number of volunteers involved in the ER project alone is double the number of volunteers involved in all the three projects.
• 17 volunteers are involved in the TR project. ,
• The number of volunteers involved in the TR project alone is one less than the number of volunteers involved in ER project alone.
• Ten volunteers involved in the TR project are also involved in at least one more project.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
Help Distress (HD) is an NGO involved in providing assistance to people suffering from natural disasters. Currently, it has 37 volunteers. They are involved in three projects: Tsunami Relief (TR) in Tamil Nadu, Flood Relief (FR) in Maharashtra, and Earthquake Relief (ER) in Gujarat. Each volunteer working with Help Distress has to be involved in at least one relief work project.
• A Maximum number of volunteers are involved in the FR project. Among them, the number of volunteers involved in FR project alone. is equal to the volunteers having additional involvement in the ER project.
• The number of volunteers involved in the ER project alone is double the number of volunteers involved in all the three projects.
• 17 volunteers are involved in the TR project. ,
• The number of volunteers involved in the TR project alone is one less than the number of volunteers involved in ER project alone.
• Ten volunteers involved in the TR project are also involved in at least one more project.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
Help Distress (HD) is an NGO involved in providing assistance to people suffering from natural disasters. Currently, it has 37 volunteers. They are involved in three projects: Tsunami Relief (TR) in Tamil Nadu, Flood Relief (FR) in Maharashtra, and Earthquake Relief (ER) in Gujarat. Each volunteer working with Help Distress has to be involved in at least one relief work project.
• A Maximum number of volunteers are involved in the FR project. Among them, the number of volunteers involved in FR project alone. is equal to the volunteers having additional involvement in the ER project.
• The number of volunteers involved in the ER project alone is double the number of volunteers involved in all the three projects.
• 17 volunteers are involved in the TR project. ,
• The number of volunteers involved in the TR project alone is one less than the number of volunteers involved in ER project alone.
• Ten volunteers involved in the TR project are also involved in at least one more project.
CAT/2005(DILR)
Question. 180
After some time, the volunteers who were involved in all the three projects were asked to withdraw from one project. As a result, one of the volunteers opted out of the TR project, and one opted out of the ER project, while the remaining ones involved in all the three projects opted out of the FR project. Which of the following statements, then, necessarily follows?
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
Help Distress (HD) is an NGO involved in providing assistance to people suffering from natural disasters. Currently, it has 37 volunteers. They are involved in three projects: Tsunami Relief (TR) in Tamil Nadu, Flood Relief (FR) in Maharashtra, and Earthquake Relief (ER) in Gujarat. Each volunteer working with Help Distress has to be involved in at least one relief work project.
• A Maximum number of volunteers are involved in the FR project. Among them, the number of volunteers involved in FR project alone. is equal to the volunteers having additional involvement in the ER project.
• The number of volunteers involved in the ER project alone is double the number of volunteers involved in all the three projects.
• 17 volunteers are involved in the TR project. ,
• The number of volunteers involved in the TR project alone is one less than the number of volunteers involved in ER project alone.
• Ten volunteers involved in the TR project are also involved in at least one more project.
CAT/2005(DILR)
Question. 181
After the withdrawal of volunteers, as indicated in Question 85, some new volunteers joined the NGO. Each one of them was allotted only one project in a manner such that, the number of volunteers working in one project alone for each of the three projects became identical. At that point, it was also found that the number of volunteers involved in FR and ER projects was the same as the number of volunteers involved in TR and ER projects. Which of the projects now has the highest number of volunteers?
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
The year is 2089. Beijing, London, New York, and Paris are in contention to host the 2096 Olympics. The eventual winner is determined through several rounds of voting by members of the IOC with each member representing a different city. All the four cities in contention are also represented in IOC.
• In any round of voting; the city receiving the lowest number of votes in that round gets eliminated. The survivor after the last round of voting gets to host the event.
• A member is allowed to cast votes for at most two different cities in all rounds of voting combined. (Hence, a member becomes ineligible to cast a vote in a given round if both the cities(s) he voted for in earlier rounds are out of contention in that round of voting.)
• A member is also ineligible to cast a vote in a round if the city(s) he represents is in contention in that round of voting.
• As long as the member is eligible,(s)he must vote and vote for only one candidate city in any round of voting.
The following incomplete table shows the information on cities that received the maximum and minimum votes in different rounds, the number of votes cast in their favour, and the total votes that were cast in those rounds.

It is also known that :
• All those who voted for London and Paris in round 1, continued to vote for the same cities in subsequent rounds as long as these cities were in contention. 75% of those who voted for Beijing in round 1, voted for Beijing in round 2 as well.
• Those who voted for New York in round 1, voted either for Beijing or Paris in round 2.
• The difference in votes cast for the two contending cities in the last round was 1.
• 50% of those who voted for Beijing in round 1, voted for Paris in round 3.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
The year is 2089. Beijing, London, New York, and Paris are in contention to host the 2096 Olympics. The eventual winner is determined through several rounds of voting by members of the IOC with each member representing a different city. All the four cities in contention are also represented in IOC.
• In any round of voting; the city receiving the lowest number of votes in that round gets eliminated. The survivor after the last round of voting gets to host the event.
• A member is allowed to cast votes for at most two different cities in all rounds of voting combined. (Hence, a member becomes ineligible to cast a vote in a given round if both the cities(s) he voted for in earlier rounds are out of contention in that round of voting.)
• A member is also ineligible to cast a vote in a round if the city(s) he represents is in contention in that round of voting.
• As long as the member is eligible,(s)he must vote and vote for only one candidate city in any round of voting.
The following incomplete table shows the information on cities that received the maximum and minimum votes in different rounds, the number of votes cast in their favour, and the total votes that were cast in those rounds.

It is also known that :
• All those who voted for London and Paris in round 1, continued to vote for the same cities in subsequent rounds as long as these cities were in contention. 75% of those who voted for Beijing in round 1, voted for Beijing in round 2 as well.
• Those who voted for New York in round 1, voted either for Beijing or Paris in round 2.
• The difference in votes cast for the two contending cities in the last round was 1.
• 50% of those who voted for Beijing in round 1, voted for Paris in round 3.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
The year is 2089. Beijing, London, New York, and Paris are in contention to host the 2096 Olympics. The eventual winner is determined through several rounds of voting by members of the IOC with each member representing a different city. All the four cities in contention are also represented in IOC.
• In any round of voting; the city receiving the lowest number of votes in that round gets eliminated. The survivor after the last round of voting gets to host the event.
• A member is allowed to cast votes for at most two different cities in all rounds of voting combined. (Hence, a member becomes ineligible to cast a vote in a given round if both the cities(s) he voted for in earlier rounds are out of contention in that round of voting.)
• A member is also ineligible to cast a vote in a round if the city(s) he represents is in contention in that round of voting.
• As long as the member is eligible,(s)he must vote and vote for only one candidate city in any round of voting.
The following incomplete table shows the information on cities that received the maximum and minimum votes in different rounds, the number of votes cast in their favour, and the total votes that were cast in those rounds.

It is also known that :
• All those who voted for London and Paris in round 1, continued to vote for the same cities in subsequent rounds as long as these cities were in contention. 75% of those who voted for Beijing in round 1, voted for Beijing in round 2 as well.
• Those who voted for New York in round 1, voted either for Beijing or Paris in round 2.
• The difference in votes cast for the two contending cities in the last round was 1.
• 50% of those who voted for Beijing in round 1, voted for Paris in round 3.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
The year is 2089. Beijing, London, New York, and Paris are in contention to host the 2096 Olympics. The eventual winner is determined through several rounds of voting by members of the IOC with each member representing a different city. All the four cities in contention are also represented in IOC.
• In any round of voting; the city receiving the lowest number of votes in that round gets eliminated. The survivor after the last round of voting gets to host the event.
• A member is allowed to cast votes for at most two different cities in all rounds of voting combined. (Hence, a member becomes ineligible to cast a vote in a given round if both the cities(s) he voted for in earlier rounds are out of contention in that round of voting.)
• A member is also ineligible to cast a vote in a round if the city(s) he represents is in contention in that round of voting.
• As long as the member is eligible,(s)he must vote and vote for only one candidate city in any round of voting.
The following incomplete table shows the information on cities that received the maximum and minimum votes in different rounds, the number of votes cast in their favour, and the total votes that were cast in those rounds.

It is also known that :
• All those who voted for London and Paris in round 1, continued to vote for the same cities in subsequent rounds as long as these cities were in contention. 75% of those who voted for Beijing in round 1, voted for Beijing in round 2 as well.
• Those who voted for New York in round 1, voted either for Beijing or Paris in round 2.
• The difference in votes cast for the two contending cities in the last round was 1.
• 50% of those who voted for Beijing in round 1, voted for Paris in round 3.
Comprehension
Directions for Questions: Answer the questions on the information given below.
In an examination, there are 100 questions divided into three groups A, B and C such that each group contains at least one question. Each question in group A carries 1 mark, each question in group B carries 2 marks and each question in group C carries 3 marks. It is known that the question in group A together carry at least 60% of the total marks.
Comprehension
Directions for Questions: Answer the questions on the information given below.
In an examination, there are 100 questions divided into three groups A, B and C such that each group contains at least one question. Each question in group A carries 1 mark, each question in group B carries 2 marks and each question in group C carries 3 marks. It is known that the question in group A together carry at least 60% of the total marks.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below
Coach John sat with the score cards of Indian players from the 3 games in a one-day cricket tournament where the same set of players played for India and all the major batsman got out. John summarized the batting performance through three diagrams, one for each game. In each diagram, the three outer triangles communicate the number of runs scored by the three top scorers from India, where K, R, S, V, and Y represent Kaif, Rahul, Saurav, Virender, and Yuvraj respectively. The middle triangle in each diagram denotes the percentage of total score that was scored by the top three Indian scorers in that game. No two players score the same number of runs in the same game. John also calculated two batting indices for each player based on his scores in the tournament; the R-index of a batsman is the difference between his higest and lowest scores in the 3 games while the M-index is the middle number, if his scores are arranged in a non-increasing order.

Comprehension
Directions for Questions: Answer the questions on the basis of the information given below
Coach John sat with the score cards of Indian players from the 3 games in a one-day cricket tournament where the same set of players played for India and all the major batsman got out. John summarized the batting performance through three diagrams, one for each game. In each diagram, the three outer triangles communicate the number of runs scored by the three top scorers from India, where K, R, S, V, and Y represent Kaif, Rahul, Saurav, Virender, and Yuvraj respectively. The middle triangle in each diagram denotes the percentage of total score that was scored by the top three Indian scorers in that game. No two players score the same number of runs in the same game. John also calculated two batting indices for each player based on his scores in the tournament; the R-index of a batsman is the difference between his higest and lowest scores in the 3 games while the M-index is the middle number, if his scores are arranged in a non-increasing order.

Comprehension
Directions for Questions: Answer the questions on the basis of the information given below
Coach John sat with the score cards of Indian players from the 3 games in a one-day cricket tournament where the same set of players played for India and all the major batsman got out. John summarized the batting performance through three diagrams, one for each game. In each diagram, the three outer triangles communicate the number of runs scored by the three top scorers from India, where K, R, S, V, and Y represent Kaif, Rahul, Saurav, Virender, and Yuvraj respectively. The middle triangle in each diagram denotes the percentage of total score that was scored by the top three Indian scorers in that game. No two players score the same number of runs in the same game. John also calculated two batting indices for each player based on his scores in the tournament; the R-index of a batsman is the difference between his higest and lowest scores in the 3 games while the M-index is the middle number, if his scores are arranged in a non-increasing order.

Comprehension
Directions for Questions: Answer the questions on the basis of the information given below
Coach John sat with the score cards of Indian players from the 3 games in a one-day cricket tournament where the same set of players played for India and all the major batsman got out. John summarized the batting performance through three diagrams, one for each game. In each diagram, the three outer triangles communicate the number of runs scored by the three top scorers from India, where K, R, S, V, and Y represent Kaif, Rahul, Saurav, Virender, and Yuvraj respectively. The middle triangle in each diagram denotes the percentage of total score that was scored by the top three Indian scorers in that game. No two players score the same number of runs in the same game. John also calculated two batting indices for each player based on his scores in the tournament; the R-index of a batsman is the difference between his higest and lowest scores in the 3 games while the M-index is the middle number, if his scores are arranged in a non-increasing order.

Comprehension
Directions for Questions: Answer the questions on the basis of the information given below
Twenty one participants from four continents (Africa, Americas, Australasia, and Europe) attended a United Nations conference. Each participant was an expert in one of four fields, labour, health, population studies, and refugee relocation. The following five facts about the participants are given..
I. The number of labour experts in the camp was exactly half the number of experts in each of the three other categories.
II. Africa did not send any labour expert. Otherwise, every continent, including Africa, sent at least one expert for each category.
III. None of the continents sent more than three experts in any category.
IV. If there had been one less Australasian expert, then the America would have had twice many experts as each of the other continents.
V. Mike and Alfanso are leading experts of population studies who attended the conference. They are from Australasia.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below
Twenty one participants from four continents (Africa, Americas, Australasia, and Europe) attended a United Nations conference. Each participant was an expert in one of four fields, labour, health, population studies, and refugee relocation. The following five facts about the participants are given..
I. The number of labour experts in the camp was exactly half the number of experts in each of the three other categories.
II. Africa did not send any labour expert. Otherwise, every continent, including Africa, sent at least one expert for each category.
III. None of the continents sent more than three experts in any category.
IV. If there had been one less Australasian expert, then the America would have had twice many experts as each of the other continents.
V. Mike and Alfanso are leading experts of population studies who attended the conference. They are from Australasia.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below
Twenty one participants from four continents (Africa, Americas, Australasia, and Europe) attended a United Nations conference. Each participant was an expert in one of four fields, labour, health, population studies, and refugee relocation. The following five facts about the participants are given..
I. The number of labour experts in the camp was exactly half the number of experts in each of the three other categories.
II. Africa did not send any labour expert. Otherwise, every continent, including Africa, sent at least one expert for each category.
III. None of the continents sent more than three experts in any category.
IV. If there had been one less Australasian expert, then the America would have had twice many experts as each of the other continents.
V. Mike and Alfanso are leading experts of population studies who attended the conference. They are from Australasia.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below
Twenty one participants from four continents (Africa, Americas, Australasia, and Europe) attended a United Nations conference. Each participant was an expert in one of four fields, labour, health, population studies, and refugee relocation. The following five facts about the participants are given..
I. The number of labour experts in the camp was exactly half the number of experts in each of the three other categories.
II. Africa did not send any labour expert. Otherwise, every continent, including Africa, sent at least one expert for each category.
III. None of the continents sent more than three experts in any category.
IV. If there had been one less Australasian expert, then the America would have had twice many experts as each of the other continents.
V. Mike and Alfanso are leading experts of population studies who attended the conference. They are from Australasia.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below
The year was 2006, All six teams in Pool A of World Cup hockey, play each other exactly once. Each win earns a team three points, a draw earns one point and a loss earns zero points. The two teams with the highest points qualify for the semifinals. In case of a tie, the team with the highest goal difference (Goal For - Goals Against) qualifies. In the opening match, Spain lost to Germany. After the second round (after each team played two matches), the pool table looked as shown below.

In the third round, Spain played Pakistan, Argentina played Germany, and New Zealand played South Africa. All the third round matches were drawn. The following are some results from the fourth and fifth round matches
(A) Spain won both the fourth and fifth round matches.
(B) Both Argentina and Germany won their fifth round matches by 3 goals to 0.
(C) Pakistan won both the fourth and fifth round matches by 1 goal to 0.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below
The year was 2006, All six teams in Pool A of World Cup hockey, play each other exactly once. Each win earns a team three points, a draw earns one point and a loss earns zero points. The two teams with the highest points qualify for the semifinals. In case of a tie, the team with the highest goal difference (Goal For - Goals Against) qualifies. In the opening match, Spain lost to Germany. After the second round (after each team played two matches), the pool table looked as shown below.

In the third round, Spain played Pakistan, Argentina played Germany, and New Zealand played South Africa. All the third round matches were drawn. The following are some results from the fourth and fifth round matches
(A) Spain won both the fourth and fifth round matches.
(B) Both Argentina and Germany won their fifth round matches by 3 goals to 0.
(C) Pakistan won both the fourth and fifth round matches by 1 goal to 0.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below
The year was 2006, All six teams in Pool A of World Cup hockey, play each other exactly once. Each win earns a team three points, a draw earns one point and a loss earns zero points. The two teams with the highest points qualify for the semifinals. In case of a tie, the team with the highest goal difference (Goal For - Goals Against) qualifies. In the opening match, Spain lost to Germany. After the second round (after each team played two matches), the pool table looked as shown below.

In the third round, Spain played Pakistan, Argentina played Germany, and New Zealand played South Africa. All the third round matches were drawn. The following are some results from the fourth and fifth round matches
(A) Spain won both the fourth and fifth round matches.
(B) Both Argentina and Germany won their fifth round matches by 3 goals to 0.
(C) Pakistan won both the fourth and fifth round matches by 1 goal to 0.
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below
The year was 2006, All six teams in Pool A of World Cup hockey, play each other exactly once. Each win earns a team three points, a draw earns one point and a loss earns zero points. The two teams with the highest points qualify for the semifinals. In case of a tie, the team with the highest goal difference (Goal For - Goals Against) qualifies. In the opening match, Spain lost to Germany. After the second round (after each team played two matches), the pool table looked as shown below.

In the third round, Spain played Pakistan, Argentina played Germany, and New Zealand played South Africa. All the third round matches were drawn. The following are some results from the fourth and fifth round matches
(A) Spain won both the fourth and fifth round matches.
(B) Both Argentina and Germany won their fifth round matches by 3 goals to 0.
(C) Pakistan won both the fourth and fifth round matches by 1 goal to 0.
Comprehension
Directions for Questions: Study the information below and answer questions based on it
New Age Consultants have three consultants Gyani, Medha and Buddhi. The sum of the number of projects handled by Gyani and Budhi individually is equal to the number of projects in which Medha is involved. All three consultants are involved together in 6 projects. Gyani works with Medha in 14 projects. Buddhi has 2 projects with Medha but without Gyani, and 3 projects with Gyani but without Medha. The total number of projects for New Age Consultants is one less than twice the number of projects in which more than one consultant is involved.
Comprehension
Directions for Questions: Study the information below and answer questions based on it
New Age Consultants have three consultants Gyani, Medha and Buddhi. The sum of the number of projects handled by Gyani and Budhi individually is equal to the number of projects in which Medha is involved. All three consultants are involved together in 6 projects. Gyani works with Medha in 14 projects. Buddhi has 2 projects with Medha but without Gyani, and 3 projects with Gyani but without Medha. The total number of projects for New Age Consultants is one less than twice the number of projects in which more than one consultant is involved.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Some children were taking free throws at the basketball court in school during lunch break. Below are some facts about how many baskets these children shot?
(i) Ganesh shot 8 baskets less than Ashish
(ii) Dhanraj and Ramesh together shot 37 baskets
(iii) Jugraj shot 8 baskets more than Dhanraj
(iv) Ashish shot 5 baskets more than Dhanraj
(v) Ashish and Ganesh together shot 40 baskets
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Some children were taking free throws at the basketball court in school during lunch break. Below are some facts about how many baskets these children shot?
(i) Ganesh shot 8 baskets less than Ashish
(ii) Dhanraj and Ramesh together shot 37 baskets
(iii) Jugraj shot 8 baskets more than Dhanraj
(iv) Ashish shot 5 baskets more than Dhanraj
(v) Ashish and Ganesh together shot 40 baskets
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Seven versity basketball players (A, B, C, D, E, F and G) are to be honoured at a special luncheon. The players will be seated on the dais in a row. A and G have the luncheon early and so must be seated at the extreme right. B will receive the most valuable player’s trophy and so must be in the centre to facilitate presentation. C and D are bitter rivals and therefore must be seated as far apart as possible.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Seven versity basketball players (A, B, C, D, E, F and G) are to be honoured at a special luncheon. The players will be seated on the dais in a row. A and G have the luncheon early and so must be seated at the extreme right. B will receive the most valuable player’s trophy and so must be in the centre to facilitate presentation. C and D are bitter rivals and therefore must be seated as far apart as possible.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Seven versity basketball players (A, B, C, D, E, F and G) are to be honoured at a special luncheon. The players will be seated on the dais in a row. A and G have the luncheon early and so must be seated at the extreme right. B will receive the most valuable player’s trophy and so must be in the centre to facilitate presentation. C and D are bitter rivals and therefore must be seated as far apart as possible.
Comprehension
Directions for Questions: Study the information below and answer questions based on it
A, B, C, D, E and F are a group of friends. There are two housewives, one professor, one engineer, one accountant and one lawyer in the group. The lawyer is married to D, who is a housewife. No woman in the group is either an engineer or an accountant. C, the accountant, is married to F, who is a professsor. A is married to a housewife. E is not a housewife.
Comprehension
Directions for Questions: Study the information below and answer questions based on it
A, B, C, D, E and F are a group of friends. There are two housewives, one professor, one engineer, one accountant and one lawyer in the group. The lawyer is married to D, who is a housewife. No woman in the group is either an engineer or an accountant. C, the accountant, is married to F, who is a professsor. A is married to a housewife. E is not a housewife.
Comprehension
Directions for Questions: Study the information below and answer questions based on it
A, B, C, D, E and F are a group of friends. There are two housewives, one professor, one engineer, one accountant and one lawyer in the group. The lawyer is married to D, who is a housewife. No woman in the group is either an engineer or an accountant. C, the accountant, is married to F, who is a professsor. A is married to a housewife. E is not a housewife.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Rang Barsey paint Company (RBPC) is in the business of manufacturing paints, RBPC buys Red, Yellow, White, Orange and Pink paints. Orange paint can be also produced by mixing Red and Yellow paints in equal proportions. Similarly, Pink paint can also be produced by mixing equal amounts of Red and White paints. Among other paints , RBPC sells Cream paint, (formed by mixing White and Yellow in the ratio 70:30) Avocado paint (formed by mixing equal amounts of Orange and Pink paint ) and Washedorange paint (formed by mixing equal amounts of Orange and White paint.) The following table provides the price at which RBPC buys paints .

Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Rang Barsey paint Company (RBPC) is in the business of manufacturing paints, RBPC buys Red, Yellow, White, Orange and Pink paints. Orange paint can be also produced by mixing Red and Yellow paints in equal proportions. Similarly, Pink paint can also be produced by mixing equal amounts of Red and White paints. Among other paints , RBPC sells Cream paint, (formed by mixing White and Yellow in the ratio 70:30) Avocado paint (formed by mixing equal amounts of Orange and Pink paint ) and Washedorange paint (formed by mixing equal amounts of Orange and White paint.) The following table provides the price at which RBPC buys paints .

Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Rang Barsey paint Company (RBPC) is in the business of manufacturing paints, RBPC buys Red, Yellow, White, Orange and Pink paints. Orange paint can be also produced by mixing Red and Yellow paints in equal proportions. Similarly, Pink paint can also be produced by mixing equal amounts of Red and White paints. Among other paints , RBPC sells Cream paint, (formed by mixing White and Yellow in the ratio 70:30) Avocado paint (formed by mixing equal amounts of Orange and Pink paint ) and Washedorange paint (formed by mixing equal amounts of Orange and White paint.) The following table provides the price at which RBPC buys paints .

Comprehension
Directions for Questions: Study the information below and answer questions based on it.
The Head of a newly formed government desires to appoint five of the six elected members A, B, C, D, E and F to portfolios of Home, Power , Defence, Telecom and Finance, F does not want any portfolio if D gets one of the five. C wants either Home or finance or no portfolio. B says that if D gets either Power or Telecom then she must get the other one. E insists on a portfolio if A gets one.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
The Head of a newly formed government desires to appoint five of the six elected members A, B, C, D, E and F to portfolios of Home, Power , Defence, Telecom and Finance, F does not want any portfolio if D gets one of the five. C wants either Home or finance or no portfolio. B says that if D gets either Power or Telecom then she must get the other one. E insists on a portfolio if A gets one.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Five friends meet every morning at Sree sagar restaurant for an idli-vada breakfast. Each consumes a different number of idils and vadas. The number of idlis consumed are 1, 4, 5, 6 and 8 while the number of vadas consumed are 0, 1, 2, 4, and 6. Below are some more facts about who eats what and how much.
(i) The number of vadas eaten by Ignesh is three times the number of vadas consumed by the person who eats four idlis
(ii) Three persons, including the one who eats four vadas, eat without chutney
(iii) Sandeep does not take any chutney
(iv) The one who eats one idli a day does not eat any vadas or chutney. Further he is not Mukesh
(v) Daljit eats idli with chutney and also eats vada
(vi) Mukesh, who does not take chutney, eats half as many vadas as the person who eats twice as many idlis as he does
(vii) Bimal eats two more idlis than Ignesh, but Ignesh eats two more vadas than Bimal
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Five friends meet every morning at Sree sagar restaurant for an idli-vada breakfast. Each consumes a different number of idils and vadas. The number of idlis consumed are 1, 4, 5, 6 and 8 while the number of vadas consumed are 0, 1, 2, 4, and 6. Below are some more facts about who eats what and how much.
(i) The number of vadas eaten by Ignesh is three times the number of vadas consumed by the person who eats four idlis
(ii) Three persons, including the one who eats four vadas, eat without chutney
(iii) Sandeep does not take any chutney
(iv) The one who eats one idli a day does not eat any vadas or chutney. Further he is not Mukesh
(v) Daljit eats idli with chutney and also eats vada
(vi) Mukesh, who does not take chutney, eats half as many vadas as the person who eats twice as many idlis as he does
(vii) Bimal eats two more idlis than Ignesh, but Ignesh eats two more vadas than Bimal
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Five friends meet every morning at Sree sagar restaurant for an idli-vada breakfast. Each consumes a different number of idils and vadas. The number of idlis consumed are 1, 4, 5, 6 and 8 while the number of vadas consumed are 0, 1, 2, 4, and 6. Below are some more facts about who eats what and how much.
(i) The number of vadas eaten by Ignesh is three times the number of vadas consumed by the person who eats four idlis
(ii) Three persons, including the one who eats four vadas, eat without chutney
(iii) Sandeep does not take any chutney
(iv) The one who eats one idli a day does not eat any vadas or chutney. Further he is not Mukesh
(v) Daljit eats idli with chutney and also eats vada
(vi) Mukesh, who does not take chutney, eats half as many vadas as the person who eats twice as many idlis as he does
(vii) Bimal eats two more idlis than Ignesh, but Ignesh eats two more vadas than Bimal
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Five women decided to go shopping to M.G.Road, Banglore. They arrived at the designated meeting place in the following order : (1) Archana, (2) Chellamma, (3) Dhenuka, (4) Helen, and (5) Shahnaz. Each woman spent at least Rs 1000. Below are some additional facts about how much they spent during their shopping spree.
(i) The woman who spent Rs 2234 arrived before the lady who spent Rs 1193
(ii) One woman spent Rs 1340 and she was not Dhenuka
(iii) One woman spent Rs 1378 more than Chellamma
(iv) One woman spent Rs 2517 and she was not Archana
(v) Helen spent more than Dhenuka
(vi) Shahnaz spent the largest amount and Chellamma the smallest
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Five women decided to go shopping to M.G.Road, Banglore. They arrived at the designated meeting place in the following order : (1) Archana, (2) Chellamma, (3) Dhenuka, (4) Helen, and (5) Shahnaz. Each woman spent at least Rs 1000. Below are some additional facts about how much they spent during their shopping spree.
(i) The woman who spent Rs 2234 arrived before the lady who spent Rs 1193
(ii) One woman spent Rs 1340 and she was not Dhenuka
(iii) One woman spent Rs 1378 more than Chellamma
(iv) One woman spent Rs 2517 and she was not Archana
(v) Helen spent more than Dhenuka
(vi) Shahnaz spent the largest amount and Chellamma the smallest
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Five women decided to go shopping to M.G.Road, Banglore. They arrived at the designated meeting place in the following order : (1) Archana, (2) Chellamma, (3) Dhenuka, (4) Helen, and (5) Shahnaz. Each woman spent at least Rs 1000. Below are some additional facts about how much they spent during their shopping spree.
(i) The woman who spent Rs 2234 arrived before the lady who spent Rs 1193
(ii) One woman spent Rs 1340 and she was not Dhenuka
(iii) One woman spent Rs 1378 more than Chellamma
(iv) One woman spent Rs 2517 and she was not Archana
(v) Helen spent more than Dhenuka
(vi) Shahnaz spent the largest amount and Chellamma the smallest
Comprehension
Directions for Questions: Study the information below and answer questions based on it.

The plan above shows an office block for six officers A, B, C, D, E and F. Both B and C occupy offices to the right of the corridor (as one enters the office block) and A occupies an office to the left of the corridor. E and F occupy offices on opposite sides of the corridor but their offices do not face each other. The offices of C and D face each other. E does not have a corner office. F’s office is further down the corridor than A’s, but on the same side.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.

The plan above shows an office block for six officers A, B, C, D, E and F. Both B and C occupy offices to the right of the corridor (as one enters the office block) and A occupies an office to the left of the corridor. E and F occupy offices on opposite sides of the corridor but their offices do not face each other. The offices of C and D face each other. E does not have a corner office. F’s office is further down the corridor than A’s, but on the same side.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.

The plan above shows an office block for six officers A, B, C, D, E and F. Both B and C occupy offices to the right of the corridor (as one enters the office block) and A occupies an office to the left of the corridor. E and F occupy offices on opposite sides of the corridor but their offices do not face each other. The offices of C and D face each other. E does not have a corner office. F’s office is further down the corridor than A’s, but on the same side.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.

The plan above shows an office block for six officers A, B, C, D, E and F. Both B and C occupy offices to the right of the corridor (as one enters the office block) and A occupies an office to the left of the corridor. E and F occupy offices on opposite sides of the corridor but their offices do not face each other. The offices of C and D face each other. E does not have a corner office. F’s office is further down the corridor than A’s, but on the same side.
Comprehension
Directions for Questions: Study the information below and answer questions based on it

Two days (Thursday and Friday) are left for campaigning before a major election, and the city administration has received requests from five political parties for taking out their processions along the following routes.
Congress : A-C-D-E BJP :A-B-D-E SP : A-B-C-E
BSP : B-C-E CPM : A-C-D
Street B-D cannot be used for a political procession on Thursday due to a religious procession. The district administration has a policy of not allowing more than one procession to pass along the same street on the same day. However, the administration must allow all parties to take out their processions during these two days.
Comprehension
Directions for Questions: Study the information below and answer questions based on it

Two days (Thursday and Friday) are left for campaigning before a major election, and the city administration has received requests from five political parties for taking out their processions along the following routes.
Congress : A-C-D-E BJP :A-B-D-E SP : A-B-C-E
BSP : B-C-E CPM : A-C-D
Street B-D cannot be used for a political procession on Thursday due to a religious procession. The district administration has a policy of not allowing more than one procession to pass along the same street on the same day. However, the administration must allow all parties to take out their processions during these two days.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Seven faculty members at a management institute frequent a lounge for strong coffee and stimulating conversation. On being asked about their visit to the lounge last Friday we got the following responses.
JC : I came in first, and the next two persons to enter were SS and SM. When I left the lounge, JP and VR were present in the lounge. DG left with me
JP : When I entered the lounge with VR, JC was sitting here. There was someone else, but I cannot remember who it was
SM :I went to the lounge for a short while, and met JC, SS, and DG in the lounge that day
SS : I left immediately after SM left
DG : I met JC, SS, SM, JP and VR during my first visit to the lounge. I went back to my office with JC. When I went to the lounge the second time, JP and VR were there
PK : I had some urgent work, so I did not sit in the lounge that day, but just collected my coffee and left. JP and DG were the only people in the lounge while I was there
VR : No comments
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Seven faculty members at a management institute frequent a lounge for strong coffee and stimulating conversation. On being asked about their visit to the lounge last Friday we got the following responses.
JC : I came in first, and the next two persons to enter were SS and SM. When I left the lounge, JP and VR were present in the lounge. DG left with me
JP : When I entered the lounge with VR, JC was sitting here. There was someone else, but I cannot remember who it was
SM :I went to the lounge for a short while, and met JC, SS, and DG in the lounge that day
SS : I left immediately after SM left
DG : I met JC, SS, SM, JP and VR during my first visit to the lounge. I went back to my office with JC. When I went to the lounge the second time, JP and VR were there
PK : I had some urgent work, so I did not sit in the lounge that day, but just collected my coffee and left. JP and DG were the only people in the lounge while I was there
VR : No comments
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Seven faculty members at a management institute frequent a lounge for strong coffee and stimulating conversation. On being asked about their visit to the lounge last Friday we got the following responses.
JC : I came in first, and the next two persons to enter were SS and SM. When I left the lounge, JP and VR were present in the lounge. DG left with me
JP : When I entered the lounge with VR, JC was sitting here. There was someone else, but I cannot remember who it was
SM :I went to the lounge for a short while, and met JC, SS, and DG in the lounge that day
SS : I left immediately after SM left
DG : I met JC, SS, SM, JP and VR during my first visit to the lounge. I went back to my office with JC. When I went to the lounge the second time, JP and VR were there
PK : I had some urgent work, so I did not sit in the lounge that day, but just collected my coffee and left. JP and DG were the only people in the lounge while I was there
VR : No comments
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Seven faculty members at a management institute frequent a lounge for strong coffee and stimulating conversation. On being asked about their visit to the lounge last Friday we got the following responses.
JC : I came in first, and the next two persons to enter were SS and SM. When I left the lounge, JP and VR were present in the lounge. DG left with me
JP : When I entered the lounge with VR, JC was sitting here. There was someone else, but I cannot remember who it was
SM :I went to the lounge for a short while, and met JC, SS, and DG in the lounge that day
SS : I left immediately after SM left
DG : I met JC, SS, SM, JP and VR during my first visit to the lounge. I went back to my office with JC. When I went to the lounge the second time, JP and VR were there
PK : I had some urgent work, so I did not sit in the lounge that day, but just collected my coffee and left. JP and DG were the only people in the lounge while I was there
VR : No comments
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Recently, the answers of a test held nationwide were leaked to a group of unscrupulous people. The investigative agency has arrested the mastermind and nine other people A, B, C, D, E, F, G, H and I in this matter. Interrogating them, the following facts have been obtained regarding their operation. Initially the mastermind obtains the correct answer-key. All the others create their answer - key in the following manner. They obtain the answer key from one or two people who already possess the same. The people are called his/her “sources”. If the person has two sources, then he/she compares the answer-keys obtained form both sources. If the key to a question from both sources is identical, it is copied, otherwise it is left blank. If the person has only one source, he/she copies the source’s answers into his/her copy. Finally, each person compulsorily replaces one of the answers (not a blank one) with a wrong answer in his/her answer key.
The paper contained 200 questions; so the investigative agency has ruled out the possibility of two or more of them introducing wrong answers to the same question. The investigative agency has a copy of the correct answer key and has tabulated the following data. These data represent question numbers.

Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Recently, the answers of a test held nationwide were leaked to a group of unscrupulous people. The investigative agency has arrested the mastermind and nine other people A, B, C, D, E, F, G, H and I in this matter. Interrogating them, the following facts have been obtained regarding their operation. Initially the mastermind obtains the correct answer-key. All the others create their answer - key in the following manner. They obtain the answer key from one or two people who already possess the same. The people are called his/her “sources”. If the person has two sources, then he/she compares the answer-keys obtained form both sources. If the key to a question from both sources is identical, it is copied, otherwise it is left blank. If the person has only one source, he/she copies the source’s answers into his/her copy. Finally, each person compulsorily replaces one of the answers (not a blank one) with a wrong answer in his/her answer key.
The paper contained 200 questions; so the investigative agency has ruled out the possibility of two or more of them introducing wrong answers to the same question. The investigative agency has a copy of the correct answer key and has tabulated the following data. These data represent question numbers.

Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Recently, the answers of a test held nationwide were leaked to a group of unscrupulous people. The investigative agency has arrested the mastermind and nine other people A, B, C, D, E, F, G, H and I in this matter. Interrogating them, the following facts have been obtained regarding their operation. Initially the mastermind obtains the correct answer-key. All the others create their answer - key in the following manner. They obtain the answer key from one or two people who already possess the same. The people are called his/her “sources”. If the person has two sources, then he/she compares the answer-keys obtained form both sources. If the key to a question from both sources is identical, it is copied, otherwise it is left blank. If the person has only one source, he/she copies the source’s answers into his/her copy. Finally, each person compulsorily replaces one of the answers (not a blank one) with a wrong answer in his/her answer key.
The paper contained 200 questions; so the investigative agency has ruled out the possibility of two or more of them introducing wrong answers to the same question. The investigative agency has a copy of the correct answer key and has tabulated the following data. These data represent question numbers.

Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Recently, the answers of a test held nationwide were leaked to a group of unscrupulous people. The investigative agency has arrested the mastermind and nine other people A, B, C, D, E, F, G, H and I in this matter. Interrogating them, the following facts have been obtained regarding their operation. Initially the mastermind obtains the correct answer-key. All the others create their answer - key in the following manner. They obtain the answer key from one or two people who already possess the same. The people are called his/her “sources”. If the person has two sources, then he/she compares the answer-keys obtained form both sources. If the key to a question from both sources is identical, it is copied, otherwise it is left blank. If the person has only one source, he/she copies the source’s answers into his/her copy. Finally, each person compulsorily replaces one of the answers (not a blank one) with a wrong answer in his/her answer key.
The paper contained 200 questions; so the investigative agency has ruled out the possibility of two or more of them introducing wrong answers to the same question. The investigative agency has a copy of the correct answer key and has tabulated the following data. These data represent question numbers.

Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Recently, the answers of a test held nationwide were leaked to a group of unscrupulous people. The investigative agency has arrested the mastermind and nine other people A, B, C, D, E, F, G, H and I in this matter. Interrogating them, the following facts have been obtained regarding their operation. Initially the mastermind obtains the correct answer-key. All the others create their answer - key in the following manner. They obtain the answer key from one or two people who already possess the same. The people are called his/her “sources”. If the person has two sources, then he/she compares the answer-keys obtained form both sources. If the key to a question from both sources is identical, it is copied, otherwise it is left blank. If the person has only one source, he/she copies the source’s answers into his/her copy. Finally, each person compulsorily replaces one of the answers (not a blank one) with a wrong answer in his/her answer key.
The paper contained 200 questions; so the investigative agency has ruled out the possibility of two or more of them introducing wrong answers to the same question. The investigative agency has a copy of the correct answer key and has tabulated the following data. These data represent question numbers.

Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Four families decided to attend the marriage ceremony of one of their colleagues. One family has no kids, while the others have at least one kid each. Each family with kids has atleast one kid attending the marriage.
Given below is some information about the families, and who reached when to attend the marriage.
The family with 2 kids came just before the family with no kids.
Shanthi who does not have any kids reached just before Sridevi’s family
Sunil and his wife reached last with their only kid.
Anil is not the husband of Joya
Anil and Raj are fathers.
Sridevi’s and Anita’s daughter go to the same school.
Joya came before Shanthi and met Anita when she reached the venue.
Raman stays the farthest from the venue.
Raj said his son could not come because of his exams.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Four families decided to attend the marriage ceremony of one of their colleagues. One family has no kids, while the others have at least one kid each. Each family with kids has atleast one kid attending the marriage.
Given below is some information about the families, and who reached when to attend the marriage.
The family with 2 kids came just before the family with no kids.
Shanthi who does not have any kids reached just before Sridevi’s family
Sunil and his wife reached last with their only kid.
Anil is not the husband of Joya
Anil and Raj are fathers.
Sridevi’s and Anita’s daughter go to the same school.
Joya came before Shanthi and met Anita when she reached the venue.
Raman stays the farthest from the venue.
Raj said his son could not come because of his exams.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Four families decided to attend the marriage ceremony of one of their colleagues. One family has no kids, while the others have at least one kid each. Each family with kids has atleast one kid attending the marriage.
Given below is some information about the families, and who reached when to attend the marriage.
The family with 2 kids came just before the family with no kids.
Shanthi who does not have any kids reached just before Sridevi’s family
Sunil and his wife reached last with their only kid.
Anil is not the husband of Joya
Anil and Raj are fathers.
Sridevi’s and Anita’s daughter go to the same school.
Joya came before Shanthi and met Anita when she reached the venue.
Raman stays the farthest from the venue.
Raj said his son could not come because of his exams.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Four families decided to attend the marriage ceremony of one of their colleagues. One family has no kids, while the others have at least one kid each. Each family with kids has atleast one kid attending the marriage.
Given below is some information about the families, and who reached when to attend the marriage.
The family with 2 kids came just before the family with no kids.
Shanthi who does not have any kids reached just before Sridevi’s family
Sunil and his wife reached last with their only kid.
Anil is not the husband of Joya
Anil and Raj are fathers.
Sridevi’s and Anita’s daughter go to the same school.
Joya came before Shanthi and met Anita when she reached the venue.
Raman stays the farthest from the venue.
Raj said his son could not come because of his exams.
CAT/2002(DILR)
Question. 240
Four students (Ashish, Dhanraj, Felix and Sameer) sat for the Common Entrance Exam for Management (CEEM). One student got admission offers from three National Institutes of Management (NIM), another in two NIMs, the third in one NIM, while the fourth got none. Below are some of the facts about who got admission offers from how many NIMs and what is their educational background
(i) The one who is an engineer didn’t get as many admissions as Ashish
(ii) The one who got offer for admissions in two NIMs isn’t Dhanraj nor is he a chartered accountant
(iii) Sameer is an economist
(iv) Dhanraj isn’t an engineer and received more admission offers than Ashish
(v) The medical doctor got the most number of admission offers
Which one of the following statements is necessarily true?
CAT/2002(DILR)
Question. 241
Five boys went to a store to buy sweets. One boy had Rs 40. Another boy had Rs30. Two other boys had Rs20 each. The remaining boy had Rs10. Below are some more facts about the initial and final cash positions
(i) Alam started with more than Jugraj
(ii) Sandeep spent Rs 1.50 more than Daljeet
(iii) Ganesh started with more money than just only one other person
(iv) Daljeet started with 2/3 of what Sandeep started with
(v) Alam spent the most, but did not end with the least
(vi) Jugraj spent the least and ended with more than Alam or Daljeet
(vii) Ganesh spent Rs 3.50.
(viii) Alam spent 10 times more than what Ganesh did.
In the choices given below, all statements except one are false. Which one of the following statements can be true?
CAT/2002(DILR)
Question. 242
In a hospital there were 200 Diabetes, 150 Hyperglycaemia and 150 Gastro-enteritis patients. Of these, 80 patients were treated for both Diabetic and Hyperglycaemia. Sixty patients were treated for Gastro-enteritis and Hyperglycaemia, while 70 were treated for Diabetes and Gastro-enteritis. Some of these paitents have all the three diseases. Doctor Dennis treats patients with only Diabetes. Doctor Hormis treats patients with only Hyperglycaemia and Doctor Gerard treats patients with only Gastro-enteritis. Doctor Paul is a generalist. Therefore, he can treat patients with multiple diseases. Patients always prefer a specialist for their disease. If Dr. Dennis had 80 patients, then the other three doctors can be arranged in terms of the number of patients treated as
CAT/2002(DILR)
Question. 243
Three children won the prizes in the Bournvita Quiz contest. They are from the schools : Loyola, Convent and Little Flowers, which are located at different cities. Below are some of the facts about the schools, the children and the city they are from
* One of the children is Bipin
* Loyola School’s contestant did not come first
* Little Flower’s contestant was named Riaz
* Convent School is not in Hyderabad
* The contestant from Pune took third place
* The contestant from Pune is not from Loyola School
* The contestant from Bangalore did not come first
* Convent School’s contestant’s name is not Balbir
Which of the following statements is true?
CAT/2002(DILR)
Question. 244
Two boys are playing on a ground. Both the boys are less than 10 years old. Age of the younger boy is equal to the cube root of the product of the age of the two boys. If we place the digit representing the age of the younger boy to the left of the digit representing the age of the elder boy, we get the age of father of the younger boy. Similarly, if we place the digit representing the age of the elder boy to the left of the digit representing the age of the younger boy and divided the figure by 2, we get the age of mother of the younger boy. The mother of the younger boy is younger to his father, by 3 years. Then, what is the age of the younger boy
CAT/2002(DILR)
Question. 245
Flights A and B are scheduled from an airport within the next one hour. All the booked passengers of the two flights are waiting in the boarding hall after check-in. The hall has a seating capacity of 200, out of which 10% remained vacant. 40% of the waiting passengers are ladies. When boarding announcements came, passengers of flight A left the hall and boarded the flight. Seating capacity of each flight is two-third of the passengers who waited in the waiting hall for both the flights put together. Half the passengers who boarded flight A are women. After boarding for flight A, 60% of the waiting hall seats became empty. For every twenty of those who are still waiting in the hall for flight B, there is one airhostess in flight A. Then, what is the ratio of empty seats in flight B to number of airhostesses in flight A?
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
A country has the following types of traffic signals.
3 red lights = stop;
2 red lights = turn left;
1 red light = turn right;
3 green lights = go at 100 kmph speed;
2 green lights = go at 40 kmph speed;
1 green light = go at 20 kmph speed.
A motorist starts at a point on a road and follows all traffic signals literally. His car is heading towards the north. He encounters the following signals (the time mentioned in each case below is applicable after crossing the previous signal).
Starting Point - 1 green light;
after half an hour, 1st signal - 2 red & 2 green lights;
after 15 minutes, 2nd signal - 1 red light;
after half an hour, 3rd signal - 1 red & 3 green lights;
after 24 minutes, 4th signal - 2 red & 2 green lights;
after 15 minutes, 5th signal - 3 red lights;
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
A country has the following types of traffic signals.
3 red lights = stop;
2 red lights = turn left;
1 red light = turn right;
3 green lights = go at 100 kmph speed;
2 green lights = go at 40 kmph speed;
1 green light = go at 20 kmph speed.
A motorist starts at a point on a road and follows all traffic signals literally. His car is heading towards the north. He encounters the following signals (the time mentioned in each case below is applicable after crossing the previous signal).
Starting Point - 1 green light;
after half an hour, 1st signal - 2 red & 2 green lights;
after 15 minutes, 2nd signal - 1 red light;
after half an hour, 3rd signal - 1 red & 3 green lights;
after 24 minutes, 4th signal - 2 red & 2 green lights;
after 15 minutes, 5th signal - 3 red lights;
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
A country has the following types of traffic signals.
3 red lights = stop;
2 red lights = turn left;
1 red light = turn right;
3 green lights = go at 100 kmph speed;
2 green lights = go at 40 kmph speed;
1 green light = go at 20 kmph speed.
A motorist starts at a point on a road and follows all traffic signals literally. His car is heading towards the north. He encounters the following signals (the time mentioned in each case below is applicable after crossing the previous signal).
Starting Point - 1 green light;
after half an hour, 1st signal - 2 red & 2 green lights;
after 15 minutes, 2nd signal - 1 red light;
after half an hour, 3rd signal - 1 red & 3 green lights;
after 24 minutes, 4th signal - 2 red & 2 green lights;
after 15 minutes, 5th signal - 3 red lights;
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
A country has the following types of traffic signals.
3 red lights = stop;
2 red lights = turn left;
1 red light = turn right;
3 green lights = go at 100 kmph speed;
2 green lights = go at 40 kmph speed;
1 green light = go at 20 kmph speed.
A motorist starts at a point on a road and follows all traffic signals literally. His car is heading towards the north. He encounters the following signals (the time mentioned in each case below is applicable after crossing the previous signal).
Starting Point - 1 green light;
after half an hour, 1st signal - 2 red & 2 green lights;
after 15 minutes, 2nd signal - 1 red light;
after half an hour, 3rd signal - 1 red & 3 green lights;
after 24 minutes, 4th signal - 2 red & 2 green lights;
after 15 minutes, 5th signal - 3 red lights;
CAT/2002(DILR)
Question. 250
The owner of a local jewellery store hired 3 watchmen to guard his diamonds, but a thief still got in and stole some diamonds. On the way out, the thief met each watchman, one at a time. To each he gave 1/2 of the diamonds he had then, and 2 more besides. He escaped with one diamond. How many did he steal originally?
CAT/2002(DILR)
Question. 251
A rich merchant had collected many gold coins. He did not want anybody to know about them. One day, his wife asked, “How many gold coins do we have?” After pausing a moment, he replied, “Well! If I divide the coins into two unequal numbers, then 48 times the difference between the two numbers equals the difference between the squares of the two numbers.” The wife looked puzzled. Can you help the merchant’s wife by finding out how many gold coins the merchant has?
CAT/2002(DILR)
Question. 252
Shyam visited Ram on vacation. In the mornings, they both would go for yoga. In the evenings they would play tennis. To have more fun, they indulge only in one activity per day, i.e., either they went for yoga or played tennis each day. There were days when they were lazy and stayed home all day long. There were 24 mornings when they did nothing, 14 evenings when they stayed at home, and a total of 22 days when they did yoga or played tennis. For how many days Shyam stayed with Ram?
CAT/2002(DILR)
Question. 253
Six persons are playing a card game. Suresh is facing Raghubir who is to the left of Ajay and to the right of Pramod. Ajay isto the left of Dhiraj. Yogendra is to the left of Pramod. If Dhiraj exchanges his seat with Yogendra and Pramod exchanges with Raghubir, who will be sitting to the left of Dhiraj?
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
A boy is asked to put in a basket one mango when ordered ‘One’, one orange when ordered ‘Two’, one apple when ordered ‘Three’ and is asked to take out from the basket one mango and an orange when ordered ‘Four’. A sequence of orders is given as :
1 2 3 3 2 1 4 2 3 1 4 2 2 3 3 1 4 1 1 3 2 3 4
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
A boy is asked to put in a basket one mango when ordered ‘One’, one orange when ordered ‘Two’, one apple when ordered ‘Three’ and is asked to take out from the basket one mango and an orange when ordered ‘Four’. A sequence of orders is given as :
1 2 3 3 2 1 4 2 3 1 4 2 2 3 3 1 4 1 1 3 2 3 4
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
A boy is asked to put in a basket one mango when ordered ‘One’, one orange when ordered ‘Two’, one apple when ordered ‘Three’ and is asked to take out from the basket one mango and an orange when ordered ‘Four’. A sequence of orders is given as :
1 2 3 3 2 1 4 2 3 1 4 2 2 3 3 1 4 1 1 3 2 3 4
CAT/2002(DILR)
Question. 256
Three travelers are sitting around a fire, and are about to eat a meal. One of them has five small loaves of bread, the second has three small loaves of bread. The third has no food, but has eight coins. He offers to pay for some bread. They agree to share the eight loaves equally among the three travelers, and the third traveler will pay eight coins for his share of the eight loaves. All loaves were the same size. The second traveler (who had three loaves) suggests that he be paid three coins, and that the first traveler be paid five coins. The first traveler says that he should get more than five coins. How much the first traveler should get?
Comprehension
Directions for Questions: Answer the following questions based on the information given below.
Elle is three times older than Yogesh. Zaheer is half the age of Wahida. Yogesh is older than Zaheer.
Comprehension
Directions for Questions: Answer the following questions based on the information given below.
A group of three or four has to be selected from seven persons. Among the seven are two women: Fiza and Kavita, and five men : Ram, Shyam, David, Peter and Rahim. Ram would not like to be in the group if Shyam is also selected. Shyam and Rahim want to be selected together in the group. Kavita would like to be in the group only if David is also there. David, if selected, would not like Peter in the group. Ram would like to be in the group only if Peter is also there. David insists that Fiza be selected in case he is there in the group.
Comprehension
Directions for Questions: Answer the following questions based on the information given below.
A group of three or four has to be selected from seven persons. Among the seven are two women: Fiza and Kavita, and five men : Ram, Shyam, David, Peter and Rahim. Ram would not like to be in the group if Shyam is also selected. Shyam and Rahim want to be selected together in the group. Kavita would like to be in the group only if David is also there. David, if selected, would not like Peter in the group. Ram would like to be in the group only if Peter is also there. David insists that Fiza be selected in case he is there in the group.
Comprehension
Directions for Questions: Answer the following questions based on the information given below.
A group of three or four has to be selected from seven persons. Among the seven are two women: Fiza and Kavita, and five men : Ram, Shyam, David, Peter and Rahim. Ram would not like to be in the group if Shyam is also selected. Shyam and Rahim want to be selected together in the group. Kavita would like to be in the group only if David is also there. David, if selected, would not like Peter in the group. Ram would like to be in the group only if Peter is also there. David insists that Fiza be selected in case he is there in the group.
CAT/2001(DILR)
Question. 262
On her walk through the park, Hamsa collected 50 coloured leaves, all either maple or oak. She sorted them by category when she got home, and found the following :
* The number of red oak leaves with spots is even and positive
* The number of red oak leaves without any spot equals the number of red maple leaves without spots
* All non-red oak leaves have spots, and there are five times as many of them as there are red spotted oak leaves
* There are no spotted maple leaves that are not red
* There are exactly 6 red spotted maple leaves
* There are exactly 22 maple leaves that are neither spotted nor red
How many oak leaves did she collect?
CAT/2001(DILR)
Question. 263
Eight people carrying food baskets are going for a picnic on motorcycles. Their names are A, B, C, D, E, F, G and H. They have four motorcycles, M1, M2, M3, and M4 among them. They also have four food baskets O, P, Q, and R of different sizes and shapes and each can be carried only on motorcycles M1, M2, M3, or M4, respectively. No more than two persons can travel on motorcycle and no more than one bakset can be carried on a motorcycle. There are two husband - wife pairs in this group of eight people and each pair will ride on a motorcycle together. C cannot travel with A or B. E cannot travel with B or F. G cannot travel with F, or H, or D. The husband-wife pairs must carry baskets O and P. Q is with A and P is with D. F travels on M1and E travels on M2 motorcycles. G is with Q, and B cannot go with R. Who is travelling with H?
CAT/2001(DILR)
Question. 264
In a family gathering there are two males who are grandfathers and four males who are fathers. In the same gathering there are two females who are grandmothers and four females who are mothers. There is at least one grandson or granddaughter present in this gathering. There are two husband-wife pairs in this group. These can either be a grandfather and a grandmother, or a father and a mother. The single grandfather (whose wife is not present) has two grandsons and a son present. The single grandmother (whose husband is not present) has two granddaughters and a daughter present. A grandfather or a grandmother present with their spouses does not have any grandson or grand daughter present. What is the minimum number of people present in this gathering.
CAT/2001(DILR)
Question. 265
I have a total of Rs, 1000. Item A costs Rs. 110, item B costs Rs 90, C costs Rs 70, item D costs Rs 40 and item E costs Rs 45. For every item D that I purchase, I must also buy two of item B. For every item A, I must buy one of item C. For very item E, I must also buy two of item D and one of item B. For every item purchased I earn 1000 points and for every rupee not spent I earn a penalty of 1500 points. My objective is to maximise the points I earn. What is the number of items that I must purchase to maximise my points?
CAT/2001(DILR)
Question. 266
Four friends Ashok, Bashir, Chirag and Deepak are out shopping. Ashok has less money than three times the amount that Bashir has. Chirag has more money than Bashir. Deepak has an amount equal to the difference of amounts with Bashir and Chirag. Ashok has three times the money with Deepak. They each have to buy at least one shirt, or one shawl, or one sweater, or one jacket that are priced Rs 200, Rs 400, Rs 600 and Rs 1000 a piece, respectively. Chirag borrows Rs 300 from Ashok and buys a jacket. Bashir buys a sweater after borrowing Rs 100 from Ashok and is left with no money. Ashok buys three shirts . What is the costliest item that Deepak could buy with his own money?
CAT/2001(DILR)
Question. 267
In a “keep-fit” gymnasium class there are fifteen females enrolled in a weight - loss program. They all have grouped in any one of the five weight-groups W1, W2, W3, W4 and W5. One instructor is assigned to one weight-group only. Sonali, Shalini, Shubhra, and Shahira belong to the same weight-group. Sonali and Rupa are in one weight-group, Rupali and Renuka are also in one weight-group. Rupa, Radha, Renuka, Ruchika, and Ritu belong to different weight-groups. Somya cannot be with Ritu, and Tara cannot be with Radha. Komal cannot be with Radha, Somya, or Ritu. Shahira is in W1 and Somya is in W4 with Ruchika. Sweta and Jyotika cannot be with Rupali, but are in a weight-group with total membership of four. No weight-group can have more than five or less than one member. Amita, Babita, Chandrika, Deepika and Elina are instructors of weight-groups with membership sizes 5, 4, 3, 2, and 1, respectively. Who is the instrutor of Radha?
CAT/2001(DILR)
Question. 268
A king has unflinching loyalty from eight of his ministers M1 to M8, but he has to select only four to make a cabinet committee. He decides to choose these four such that each selected person shares a liking with at least one of the other three selected. The selected persons must also hate at least one of the likings of any of the other three persons selected
M1 likes fishing and smoking, but hates gambling,
M2 likes smoking and drinking, but hates fishing,
M3 likes gambling, but hates smoking,
M4 likes mountaineering , but hates drinking,
M5 likes drinking, but hates smoking and mountaineering
M6 likes fishing, but hates smoking and mountaineering
M7 likes gambling and mountaineering, but hates fishing, and
M8 likes smoking and gambling, but hates mountaineering.
Who are the four people selected by the king?
Comprehension
Directions for questions: Read the information given below and answer the questions that follow :
Answer these question based on the pipeline diagram below.
The following sketch shows the pipelines carrying material from one location to another. Each location has a demand for material. The demand at Vaishali is 400, at Jyotishmati is 400, at Panchal is 700, and at Vidisha is 200. Each arrow indicates the direction of material flow through the pipeline. The flow from Vaishali to Jyotishmati is 300. The quantity of material flow is such that the demands at all these locations are exactly met. The capacity of each pipeline is 1000.

Comprehension
Directions for questions: Read the information given below and answer the questions that follow :
Answer these question based on the pipeline diagram below.
The following sketch shows the pipelines carrying material from one location to another. Each location has a demand for material. The demand at Vaishali is 400, at Jyotishmati is 400, at Panchal is 700, and at Vidisha is 200. Each arrow indicates the direction of material flow through the pipeline. The flow from Vaishali to Jyotishmati is 300. The quantity of material flow is such that the demands at all these locations are exactly met. The capacity of each pipeline is 1000.

Comprehension
Directions for questions: Read the information given below and answer the questions that follow :
Answer these question based on the pipeline diagram below.
The following sketch shows the pipelines carrying material from one location to another. Each location has a demand for material. The demand at Vaishali is 400, at Jyotishmati is 400, at Panchal is 700, and at Vidisha is 200. Each arrow indicates the direction of material flow through the pipeline. The flow from Vaishali to Jyotishmati is 300. The quantity of material flow is such that the demands at all these locations are exactly met. The capacity of each pipeline is 1000.

CAT/2000(DILR)
Question. 272
In a bag a person can carry 10 books. The books are mathematics physics, management and fiction. If a person carries a book of management, he has to carry two or more books of fiction. If he carries a book of mathematics he has to carry two or more books of physics. In carrying books he used to get certain points. To carry a book of management, mathematics, physics and fiction each the points he got were 4, 3, 2, 1 respectively. He has to carry a book of each subject. So what is the maximum no of points a person can get
CAT/2000(DILR)
Question. 273
Five persons P, Q , T, S, M lives in a hut, palace hotel, cottage, penthouse not necessarily in tha order. Each of them like two colours out of red, green, yellow, blue and black. P likes red and blue. Q lives in a hut. T likes yellow and black and S likes the colour liked by P. The person who lives in a palace doesn’t like blue or black colour where does M stay?
CAT/2000(DILR)
Question. 274
There is a gathering to felicitate 7 cricketers T, U, V, W, X, Y, Z. They are all seated on one side of a rectangular table. V and W want to leave early and so will occupy the two positions on the extreme right of the table. T is the man of the match and hence will occupy the centre position. U and V are bitter enemies and should be seated as far as possible. Y,T and X are great friends and so must be seated always next to each other. What is the position of X?
CAT/2000(DILR)
Question. 275
Rita, Sita , Gita and Mita went to a dance party with Tarun, Arun, Varun and Karun. Rita did not dance with Tarun or Varun, Gita knew only disco dance and Arun and Varun did not know disco. Mita and Varun are bitter enemies and won’t dance with each other. Given a choice, Arun won’t dance with Mita. Karun’s partner is Gita. Who was Mita’s dance partner?
CAT/2000(DILR)
Question. 278
At a village mela, the following six nautanki (plays) are scheduled as shown in the table below

You like to see all the six nautankis. Further, you wise to ensure that you get a lunch break from 12:30 p.m. to 1:30 p.m Which of the following ways can you do this?
CAT/2000(DILR)
Question. 279
Mrs. Ranga has three children and has difficulty remembering their ages and the months of their birth. The clues below may help her remember
The boy, who was born in June, is 7 years old
One of the children is 4 years old, but it is not Anshuman
Vaibhav is older than Suprita
One of the children was born in September, but it was not Vaibhav
Supritas birthday is in April
The youngest child is only 2 years old.
Based on the above clues, which one of the following statements is true?
CAT/2000(DILR)
Question. 280
The Bannerjees, the Sharmas, and the Pattabhiramans each have a tradition of eating Sunday lunch as a family. Each family serves a special meal at a certain time of day. Each family has a particular set of chinaware used only for this meal. Use the clues below to answer the following question
* The Sharma family eats at noon
* The family that serves fried brinjal uses blue chinaware
* The Bannerjee family eats at 2 o’clock
* The family that serves sambar does not use red chinaware
* The family that eats at 1 o’clock serves fried brinjal
* The Pattabhiraman family does not use white chinaware
* The family that eats last likes makkai-ki-roti
Which one of the following statements is true?
CAT/2000(DILR)
Question. 281
While Balbir had his back turned, a dog ran into his butcher shop, snatched a piece of meat of the counter and ran out. Balbir was mad when he realised what had happened. He asked three other shopkeepers, who had seen the dog, to describe it. The shopkeepers really didn’t want to help Balbir. So each of them made a statement which contained one truth and one lie
* Shopkeeper Number 1 said - “The dog had black hair and a long tail”.
* Shopkeeper Number 2 said - “The dog had a short tail and wore a collar.”
* Shopkeeper Number 3 said- “The dog had white hair and no collar.”
Based on the above statements, which of the following could be a correct descriptions?
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
There are six people A, B, C, D, E and F. Two of them are housewives, one is an accountant, one is an architect, one is a lawyer and one is a lecturer. A, the lawyer is married to D & E is not the housewife. None of the females is the architect or the accountant. There are two married couples. C is the accounant, Married to the lecturer F.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
There are six people A, B, C, D, E and F. Two of them are housewives, one is an accountant, one is an architect, one is a lawyer and one is a lecturer. A, the lawyer is married to D & E is not the housewife. None of the females is the architect or the accountant. There are two married couples. C is the accounant, Married to the lecturer F.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Ten coins are distributed among four people P,Q,R & S such that if one person gets n coins, second gets (n+1) , third gets (n+2) and so on but not necessarily in the same order. Q gets more coins than P and S gets fewer coins than R
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Ten coins are distributed among four people P,Q,R & S such that if one person gets n coins, second gets (n+1) , third gets (n+2) and so on but not necessarily in the same order. Q gets more coins than P and S gets fewer coins than R
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Ten coins are distributed among four people P,Q,R & S such that if one person gets n coins, second gets (n+1) , third gets (n+2) and so on but not necessarily in the same order. Q gets more coins than P and S gets fewer coins than R
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Ten coins are distributed among four people P,Q,R & S such that if one person gets n coins, second gets (n+1) , third gets (n+2) and so on but not necessarily in the same order. Q gets more coins than P and S gets fewer coins than R
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Seven players A, B, C, D,E, F & G have to take dinner sitting on the same side of a rectangular table. Both A & G want to leave early so they must sit on the extreme right positions. B has to receive the man of the match award so he must sit in the middle. C & D don’t like each other so they must sit as far from each other as possible . E & F are very good friends & so they must sit together. With the help of this information answer the following questions.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Seven players A, B, C, D,E, F & G have to take dinner sitting on the same side of a rectangular table. Both A & G want to leave early so they must sit on the extreme right positions. B has to receive the man of the match award so he must sit in the middle. C & D don’t like each other so they must sit as far from each other as possible . E & F are very good friends & so they must sit together. With the help of this information answer the following questions.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
On the bank of a river there are four deities. Sandhya went there with x flowers. Before offering the flowers she dips them in the river & they get doubled. Now she offers y flowers to the first deity & dips the remaining flowers in the river so that they get doubled again. She offers y flowers to the second deity as well & repeats the same process for 3rd & 4th deity. After offering flowers to the 4th deity, she realises that she is left with no flowers at all.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
On the bank of a river there are four deities. Sandhya went there with x flowers. Before offering the flowers she dips them in the river & they get doubled. Now she offers y flowers to the first deity & dips the remaining flowers in the river so that they get doubled again. She offers y flowers to the second deity as well & repeats the same process for 3rd & 4th deity. After offering flowers to the 4th deity, she realises that she is left with no flowers at all.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
On the bank of a river there are four deities. Sandhya went there with x flowers. Before offering the flowers she dips them in the river & they get doubled. Now she offers y flowers to the first deity & dips the remaining flowers in the river so that they get doubled again. She offers y flowers to the second deity as well & repeats the same process for 3rd & 4th deity. After offering flowers to the 4th deity, she realises that she is left with no flowers at all.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Ghosh Babu goes to a casino in Kay - Kay islands where he comes across an interesting game of cards. The visitor playing the game is called the player & the clubman is called the dealer. The rules of the game are as follows: First the player picks the card. This card is called the base card & the number on the face of the card is called the base value of the card. Ace, King, Queen & Jack all have base value of 10. The dealer pays the player same number of rupees as the base value of the card. Now the dealer picks a card &. This is called the top card. If topcard is of the same suite then the player pays the dealer double the amount of base value. If it is of the same colour but not the same suite then the player pays the dealer the amount of a bse value. If it is of different colour then the dealer pays the player the amount of base value.
Ghosh Babu plays the game 4 times. First time, he draws 8 of club & the dealer draws jack of club. Second time he draws 10 of hearts & the dealer draws 2 of spade. Third time he draws 6 of diamond & the dealer draws 1 of heart. Finally, Ghosh Babu draws 8 of spade and the dealer draws ace of the spade.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Ghosh Babu goes to a casino in Kay - Kay islands where he comes across an interesting game of cards. The visitor playing the game is called the player & the clubman is called the dealer. The rules of the game are as follows: First the player picks the card. This card is called the base card & the number on the face of the card is called the base value of the card. Ace, King, Queen & Jack all have base value of 10. The dealer pays the player same number of rupees as the base value of the card. Now the dealer picks a card &. This is called the top card. If topcard is of the same suite then the player pays the dealer double the amount of base value. If it is of the same colour but not the same suite then the player pays the dealer the amount of a bse value. If it is of different colour then the dealer pays the player the amount of base value.
Ghosh Babu plays the game 4 times. First time, he draws 8 of club & the dealer draws jack of club. Second time he draws 10 of hearts & the dealer draws 2 of spade. Third time he draws 6 of diamond & the dealer draws 1 of heart. Finally, Ghosh Babu draws 8 of spade and the dealer draws ace of the spade.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Ghosh Babu goes to a casino in Kay - Kay islands where he comes across an interesting game of cards. The visitor playing the game is called the player & the clubman is called the dealer. The rules of the game are as follows: First the player picks the card. This card is called the base card & the number on the face of the card is called the base value of the card. Ace, King, Queen & Jack all have base value of 10. The dealer pays the player same number of rupees as the base value of the card. Now the dealer picks a card &. This is called the top card. If topcard is of the same suite then the player pays the dealer double the amount of base value. If it is of the same colour but not the same suite then the player pays the dealer the amount of a bse value. If it is of different colour then the dealer pays the player the amount of base value.
Ghosh Babu plays the game 4 times. First time, he draws 8 of club & the dealer draws jack of club. Second time he draws 10 of hearts & the dealer draws 2 of spade. Third time he draws 6 of diamond & the dealer draws 1 of heart. Finally, Ghosh Babu draws 8 of spade and the dealer draws ace of the spade.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.

For a truck that can carry 2000 cubic feet, hiring cost per day is Rs 1000. Storing cost per cubic feet is Rs 5 per day.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.

For a truck that can carry 2000 cubic feet, hiring cost per day is Rs 1000. Storing cost per cubic feet is Rs 5 per day.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
A, B, C, D are to be seated in a row. But C and D cannot be together. Also B cannot be at the third place.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
A, B, C, D collected one rupee coins following the given pattern.
(i) Together they collected 100 coins
(ii) Each one of them collected even no. of coins
(iii) Each one of them collected at least 10 coins
(iv) No two of them collected the same no. of coins
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
A, B, C, D collected one rupee coins following the given pattern.
(i) Together they collected 100 coins
(ii) Each one of them collected even no. of coins
(iii) Each one of them collected at least 10 coins
(iv) No two of them collected the same no. of coins
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
A, B, C, D collected one rupee coins following the given pattern.
(i) Together they collected 100 coins
(ii) Each one of them collected even no. of coins
(iii) Each one of them collected at least 10 coins
(iv) No two of them collected the same no. of coins
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Amar, Akbar, Anthony are three friends. Only three colors are available for their shirts, viz. Red, Green and Blue. Amar did not wear red shirt. Akbar did not wear green shirt. Anthony did not wear blue shirt.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Amar, Akbar, Anthony are three friends. Only three colors are available for their shirts, viz. Red, Green and Blue. Amar did not wear red shirt. Akbar did not wear green shirt. Anthony did not wear blue shirt.
CAT/1998(DILR)
Question. 305
If two of them wear the same colour then how many of the following must be false
I. Amar wears blue and Akbar does not wear green
II. Amar does not wear blue and Akbar wears blue.
III. Amar does not wear blue and Akbar does not wear blue
IV. Amar wears green. Akbar does not wear red. Anthony does not wear green
CAT/1998(DILR)
Question. 306
My son adores chocolates. He likes biscuits. But he hates apples. I told him that he can buy as many chocolates he wishes. But then he must have biscuits twice the number of chocolates and apples more than biscuits and chocolates together. Each chocolate costs Re. 1. The cost of apple is twice of chocolate and four biscuits are worth of one apple. Then which of the following can be the amount that I spent on that evening on my son?
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Bankatlal acted as a judge for the beauty contest. There were four participants, viz. Ms. Andhra Pradesh, Ms. Uttar Pradesh, Ms. West Bengal and Ms. Maharashtra. Mrs. Bankatlal, who was very anxious about the result asked him about it as soon as he was back home. Bankatlal just told that the one who was wearing the yellow saree won the contest. When Mrs. Bankatlal pressed for further details, he elaborated as follows:
I. All of them were sitting in a row
II. All of them wore sarees of different colors, viz. Green, Yellow, White, Red
III. There was only one runner up and she was sitting beside Ms. Maharashtra
IV. The runner up was wearing the Green saree
V. Ms. West Bengal was not sitting at the ends and was not a runner up
VI. The winner and the runner up are not sitting adjacent to each other
VII. Ms. Maharashtra was wearing white saree
VIII. Ms. Andhra Pradesh was not wearing the Green saree
IX. Participants wearing Yellow saree and White saree were at the ends
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Bankatlal acted as a judge for the beauty contest. There were four participants, viz. Ms. Andhra Pradesh, Ms. Uttar Pradesh, Ms. West Bengal and Ms. Maharashtra. Mrs. Bankatlal, who was very anxious about the result asked him about it as soon as he was back home. Bankatlal just told that the one who was wearing the yellow saree won the contest. When Mrs. Bankatlal pressed for further details, he elaborated as follows:
I. All of them were sitting in a row
II. All of them wore sarees of different colors, viz. Green, Yellow, White, Red
III. There was only one runner up and she was sitting beside Ms. Maharashtra
IV. The runner up was wearing the Green saree
V. Ms. West Bengal was not sitting at the ends and was not a runner up
VI. The winner and the runner up are not sitting adjacent to each other
VII. Ms. Maharashtra was wearing white saree
VIII. Ms. Andhra Pradesh was not wearing the Green saree
IX. Participants wearing Yellow saree and White saree were at the ends
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Bankatlal acted as a judge for the beauty contest. There were four participants, viz. Ms. Andhra Pradesh, Ms. Uttar Pradesh, Ms. West Bengal and Ms. Maharashtra. Mrs. Bankatlal, who was very anxious about the result asked him about it as soon as he was back home. Bankatlal just told that the one who was wearing the yellow saree won the contest. When Mrs. Bankatlal pressed for further details, he elaborated as follows:
I. All of them were sitting in a row
II. All of them wore sarees of different colors, viz. Green, Yellow, White, Red
III. There was only one runner up and she was sitting beside Ms. Maharashtra
IV. The runner up was wearing the Green saree
V. Ms. West Bengal was not sitting at the ends and was not a runner up
VI. The winner and the runner up are not sitting adjacent to each other
VII. Ms. Maharashtra was wearing white saree
VIII. Ms. Andhra Pradesh was not wearing the Green saree
IX. Participants wearing Yellow saree and White saree were at the ends
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Bankatlal acted as a judge for the beauty contest. There were four participants, viz. Ms. Andhra Pradesh, Ms. Uttar Pradesh, Ms. West Bengal and Ms. Maharashtra. Mrs. Bankatlal, who was very anxious about the result asked him about it as soon as he was back home. Bankatlal just told that the one who was wearing the yellow saree won the contest. When Mrs. Bankatlal pressed for further details, he elaborated as follows:
I. All of them were sitting in a row
II. All of them wore sarees of different colors, viz. Green, Yellow, White, Red
III. There was only one runner up and she was sitting beside Ms. Maharashtra
IV. The runner up was wearing the Green saree
V. Ms. West Bengal was not sitting at the ends and was not a runner up
VI. The winner and the runner up are not sitting adjacent to each other
VII. Ms. Maharashtra was wearing white saree
VIII. Ms. Andhra Pradesh was not wearing the Green saree
IX. Participants wearing Yellow saree and White saree were at the ends
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Krishna distributed 10 acre of land to Gopal and Ram who paid him the total amount in the ratio 2:3. Gopal invested further Rs2 lac in the land and planted coconut and lemon trees in the ratio 5:1 on equal area of land. There were a total of 100 lemon trees. The cost of one coconut was Rs 5. The crop took 7 years to mature and when the crop was reaped in 1997, the total revenue generated was 25% of the total amount put in by Gopal and Ram together. The revenue generated from the coconut and lemon tress was in the ratio 3:2 and it was shared equally by Gopal and Ram as the initial amount spent by them were equal.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Krishna distributed 10 acre of land to Gopal and Ram who paid him the total amount in the ratio 2:3. Gopal invested further Rs2 lac in the land and planted coconut and lemon trees in the ratio 5:1 on equal area of land. There were a total of 100 lemon trees. The cost of one coconut was Rs 5. The crop took 7 years to mature and when the crop was reaped in 1997, the total revenue generated was 25% of the total amount put in by Gopal and Ram together. The revenue generated from the coconut and lemon tress was in the ratio 3:2 and it was shared equally by Gopal and Ram as the initial amount spent by them were equal.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Krishna distributed 10 acre of land to Gopal and Ram who paid him the total amount in the ratio 2:3. Gopal invested further Rs2 lac in the land and planted coconut and lemon trees in the ratio 5:1 on equal area of land. There were a total of 100 lemon trees. The cost of one coconut was Rs 5. The crop took 7 years to mature and when the crop was reaped in 1997, the total revenue generated was 25% of the total amount put in by Gopal and Ram together. The revenue generated from the coconut and lemon tress was in the ratio 3:2 and it was shared equally by Gopal and Ram as the initial amount spent by them were equal.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Krishna distributed 10 acre of land to Gopal and Ram who paid him the total amount in the ratio 2:3. Gopal invested further Rs2 lac in the land and planted coconut and lemon trees in the ratio 5:1 on equal area of land. There were a total of 100 lemon trees. The cost of one coconut was Rs 5. The crop took 7 years to mature and when the crop was reaped in 1997, the total revenue generated was 25% of the total amount put in by Gopal and Ram together. The revenue generated from the coconut and lemon tress was in the ratio 3:2 and it was shared equally by Gopal and Ram as the initial amount spent by them were equal.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Krishna distributed 10 acre of land to Gopal and Ram who paid him the total amount in the ratio 2:3. Gopal invested further Rs2 lac in the land and planted coconut and lemon trees in the ratio 5:1 on equal area of land. There were a total of 100 lemon trees. The cost of one coconut was Rs 5. The crop took 7 years to mature and when the crop was reaped in 1997, the total revenue generated was 25% of the total amount put in by Gopal and Ram together. The revenue generated from the coconut and lemon tress was in the ratio 3:2 and it was shared equally by Gopal and Ram as the initial amount spent by them were equal.
Comprehension
Directions for Questions: Answer the following questions based on the information given below.
Elle is three times older than Yogesh. Zaheer is half the age of Wahida. Yogesh is older than Zaheer.
Comprehension
Directions for Questions : Study the information below and answer questions based on it.
A certain race is made up of three stretches A, B and C, each 2 km long, and to be covered by a certain mode of transport. The following table gives these modes of transport for the stretches, and the minimum and maximum possible speeds (in kmph) over these stretches. The speed over a particular stretch is assumed to be constant. The previous record for the race is ten minutes.

Comprehension
Directions for Questions : Study the information below and answer questions based on it.
A certain race is made up of three stretches A, B and C, each 2 km long, and to be covered by a certain mode of transport. The following table gives these modes of transport for the stretches, and the minimum and maximum possible speeds (in kmph) over these stretches. The speed over a particular stretch is assumed to be constant. The previous record for the race is ten minutes.

Comprehension
Directions for Questions : Study the information below and answer questions based on it.
A certain race is made up of three stretches A, B and C, each 2 km long, and to be covered by a certain mode of transport. The following table gives these modes of transport for the stretches, and the minimum and maximum possible speeds (in kmph) over these stretches. The speed over a particular stretch is assumed to be constant. The previous record for the race is ten minutes.

Comprehension
Directions for Questions : Study the information below and answer questions based on it.
The Weirdo Holiday Resort follows a particular system of holidays for its employees. People are given holidays on the days where the first letter of the day of the week is the same as the first letter of their names. All employees work at the same rate.
Comprehension
Directions for Questions : Study the information below and answer questions based on it.
The Weirdo Holiday Resort follows a particular system of holidays for its employees. People are given holidays on the days where the first letter of the day of the week is the same as the first letter of their names. All employees work at the same rate.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
A manufacturer can choose from any of the three types of tests available for checking the quality of his product. The graph that follows gives the relative costs for each of these tests for a given percentage of defective pieces.

Comprehension
Directions for Questions: Study the information below and answer questions based on it.
A manufacturer can choose from any of the three types of tests available for checking the quality of his product. The graph that follows gives the relative costs for each of these tests for a given percentage of defective pieces.

Comprehension
Directions for Questions: Study the information below and answer questions based on it.
A manufacturer can choose from any of the three types of tests available for checking the quality of his product. The graph that follows gives the relative costs for each of these tests for a given percentage of defective pieces.

Comprehension
Directions for Questions: Study the information below and answer questions based on it.
A manufacturer can choose from any of the three types of tests available for checking the quality of his product. The graph that follows gives the relative costs for each of these tests for a given percentage of defective pieces.

Comprehension
Directions for Questions: Study the information below and answer questions based on it.
A manufacturer can choose from any of the three types of tests available for checking the quality of his product. The graph that follows gives the relative costs for each of these tests for a given percentage of defective pieces.

Comprehension
Directions for Questions : Study the information below and answer questions based on it.
In a locality, there are five small towns, A, B, C, D and E. The distances of these towns from each other are as follows:
AB = 2 km AC = 2km AD > 2km AE > 3km BC = 2km BD = 4 km BE = 3km CD = 2km CE= 3km DE > 3km
Comprehension
Directions for Questions : Study the information below and answer questions based on it.
In a locality, there are five small towns, A, B, C, D and E. The distances of these towns from each other are as follows:
AB = 2 km AC = 2km AD > 2km AE > 3km BC = 2km BD = 4 km BE = 3km CD = 2km CE= 3km DE > 3km
Comprehension
Directions for Questions: Study the information below and answer questions based on it:
Four sisters Suvarna, Tara, Uma and Vibha are playing a game such that the loser doubles the money of each of the other player. They played four games and each sister lost one game in alphabetical order. At the end of fourth game each sister had Rs 32.
Comprehension
Directions for Questions: Study the information below and answer questions based on it:
Four sisters Suvarna, Tara, Uma and Vibha are playing a game such that the loser doubles the money of each of the other player. They played four games and each sister lost one game in alphabetical order. At the end of fourth game each sister had Rs 32.
Comprehension
Directions for Questions: Study the information below and answer questions based on it:
Four sisters Suvarna, Tara, Uma and Vibha are playing a game such that the loser doubles the money of each of the other player. They played four games and each sister lost one game in alphabetical order. At the end of fourth game each sister had Rs 32.
Comprehension
Directions for Questions: Study the information below and answer questions based on it:
Four sisters Suvarna, Tara, Uma and Vibha are playing a game such that the loser doubles the money of each of the other player. They played four games and each sister lost one game in alphabetical order. At the end of fourth game each sister had Rs 32.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Machine M1 as well as Machine M2 can independently produce either Product P or Product Q. The times taken by machines M1 and M2 (in minutes ) to produce one unit of product P and Q are given in the table below : (Each machine works 8 hours per day).

Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Machine M1 as well as Machine M2 can independently produce either Product P or Product Q. The times taken by machines M1 and M2 (in minutes ) to produce one unit of product P and Q are given in the table below : (Each machine works 8 hours per day).

Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Machine M1 as well as Machine M2 can independently produce either Product P or Product Q. The times taken by machines M1 and M2 (in minutes ) to produce one unit of product P and Q are given in the table below : (Each machine works 8 hours per day).

Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Machine M1 as well as Machine M2 can independently produce either Product P or Product Q. The times taken by machines M1 and M2 (in minutes ) to produce one unit of product P and Q are given in the table below : (Each machine works 8 hours per day).

Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Machine M1 as well as Machine M2 can independently produce either Product P or Product Q. The times taken by machines M1 and M2 (in minutes ) to produce one unit of product P and Q are given in the table below : (Each machine works 8 hours per day).

Comprehension
Directions for Questions: Study the information below and answer questions based on it:
A leading socialite decided to organise a dinner and invited a few of her friends. Only the host and the hostess were sitting at the opposite ends of a rectangular table, with three persons along each side. The pre-requisite for the seating arrangement was that each person must be seated such that atleast on one side it has a person of opposite sex. Maqbool is opposite Shobha, who is not the hostess. Ratan has a woman on his right and is sitting opposite a woman. Monisha is sitting to the hostess’s right, next to Dhirubhai. One person is seated between Madhuri and Urmila who is not the hostess. The men were Maqbool, Ratan, Dhirubhai and Jackie, while the women were Madhuri, Urmila, Shobha and Monisha.
Comprehension
Directions for Questions: Study the information below and answer questions based on it:
A leading socialite decided to organise a dinner and invited a few of her friends. Only the host and the hostess were sitting at the opposite ends of a rectangular table, with three persons along each side. The pre-requisite for the seating arrangement was that each person must be seated such that atleast on one side it has a person of opposite sex. Maqbool is opposite Shobha, who is not the hostess. Ratan has a woman on his right and is sitting opposite a woman. Monisha is sitting to the hostess’s right, next to Dhirubhai. One person is seated between Madhuri and Urmila who is not the hostess. The men were Maqbool, Ratan, Dhirubhai and Jackie, while the women were Madhuri, Urmila, Shobha and Monisha.
Comprehension
Directions for Questions: Study the information below and answer questions based on it:
A leading socialite decided to organise a dinner and invited a few of her friends. Only the host and the hostess were sitting at the opposite ends of a rectangular table, with three persons along each side. The pre-requisite for the seating arrangement was that each person must be seated such that atleast on one side it has a person of opposite sex. Maqbool is opposite Shobha, who is not the hostess. Ratan has a woman on his right and is sitting opposite a woman. Monisha is sitting to the hostess’s right, next to Dhirubhai. One person is seated between Madhuri and Urmila who is not the hostess. The men were Maqbool, Ratan, Dhirubhai and Jackie, while the women were Madhuri, Urmila, Shobha and Monisha.
CAT/1994(DILR)
Question. 340
If Ratan would have exchanged seats with a person four places to his left, which of the following would have been true after the exchange?
I. No one was seated between two persons of the opposite sex. (e.g. no man was seated between two women)
II. One side of the table consisted entirely of persons of the same sex.
III. Either the host or the hostess changed seats.
Comprehension
Directions for Questions: Study the information below and answer questions based on it:
A leading socialite decided to organise a dinner and invited a few of her friends. Only the host and the hostess were sitting at the opposite ends of a rectangular table, with three persons along each side. The pre-requisite for the seating arrangement was that each person must be seated such that atleast on one side it has a person of opposite sex. Maqbool is opposite Shobha, who is not the hostess. Ratan has a woman on his right and is sitting opposite a woman. Monisha is sitting to the hostess’s right, next to Dhirubhai. One person is seated between Madhuri and Urmila who is not the hostess. The men were Maqbool, Ratan, Dhirubhai and Jackie, while the women were Madhuri, Urmila, Shobha and Monisha.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Five of India’s leading models are posing for a photograph promoting “y’know, world peace and understanding”. But then, Rakesh Shreshtha the photographer is having a tough time getting them to stand in a straight line, because Aishwarya refused to stand next to Sushmita because Sushmita had said something about her in a leading gossip magazine. Rachel and Anu want to stand together because they are “such good griends, y’know”. Manpreet on the other hand cannot get along well with Rachel, because there is some talk about Rachel scheming to get a contract already awarded to Manpreet. Anu believes her friendly astrologer who has asked her to stand at the extreme right for all group photographs. Finally, Rakesh managed to pacify the girls and got a beautiful picture of five beautiful girls smiling beautifully in a beautiful straight line, promoting world peace.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Five of India’s leading models are posing for a photograph promoting “y’know, world peace and understanding”. But then, Rakesh Shreshtha the photographer is having a tough time getting them to stand in a straight line, because Aishwarya refused to stand next to Sushmita because Sushmita had said something about her in a leading gossip magazine. Rachel and Anu want to stand together because they are “such good griends, y’know”. Manpreet on the other hand cannot get along well with Rachel, because there is some talk about Rachel scheming to get a contract already awarded to Manpreet. Anu believes her friendly astrologer who has asked her to stand at the extreme right for all group photographs. Finally, Rakesh managed to pacify the girls and got a beautiful picture of five beautiful girls smiling beautifully in a beautiful straight line, promoting world peace.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Five of India’s leading models are posing for a photograph promoting “y’know, world peace and understanding”. But then, Rakesh Shreshtha the photographer is having a tough time getting them to stand in a straight line, because Aishwarya refused to stand next to Sushmita because Sushmita had said something about her in a leading gossip magazine. Rachel and Anu want to stand together because they are “such good griends, y’know”. Manpreet on the other hand cannot get along well with Rachel, because there is some talk about Rachel scheming to get a contract already awarded to Manpreet. Anu believes her friendly astrologer who has asked her to stand at the extreme right for all group photographs. Finally, Rakesh managed to pacify the girls and got a beautiful picture of five beautiful girls smiling beautifully in a beautiful straight line, promoting world peace.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
A, B, C, D, E, F and G are brothers. Two brothers had an argument and A said to B “You are as old as C was when I was twice as old as D, and will be as old as E was when he was as old as C is now”. B said to A, “You may be older than F but G is as old as I was when you were as old as G is, and D will be as old as F was when F will be as old as G is”.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
A, B, C, D, E, F and G are brothers. Two brothers had an argument and A said to B “You are as old as C was when I was twice as old as D, and will be as old as E was when he was as old as C is now”. B said to A, “You may be older than F but G is as old as I was when you were as old as G is, and D will be as old as F was when F will be as old as G is”.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
A, B, C, D, E, F and G are brothers. Two brothers had an argument and A said to B “You are as old as C was when I was twice as old as D, and will be as old as E was when he was as old as C is now”. B said to A, “You may be older than F but G is as old as I was when you were as old as G is, and D will be as old as F was when F will be as old as G is”.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
A, B, C, D, E, F and G are brothers. Two brothers had an argument and A said to B “You are as old as C was when I was twice as old as D, and will be as old as E was when he was as old as C is now”. B said to A, “You may be older than F but G is as old as I was when you were as old as G is, and D will be as old as F was when F will be as old as G is”.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
The primitive tribes-folk of the island of Lexicophobos have recently developed a language for themselves, which has a very limited vocabulary. In fact, the words can be classified into only three types : the Bingoes, the Cingoes and the Dingoes.
The Bingoes type of words are : Grumbs, Harrumphs, Ihavitoo
The Cingoes type of words are : Ihavitoo, Jingongo, Koolodo
The Dingoes type of words are : Lovitoo, Metoo, Nana
They have also devised some rules of grammar :
I. Every sentence must have only five words
II. Every sentence must have two Bingoes, one Cingo and two Dingoes.
III. If Grumbs is used in a sentence, Ihavitoo must also be used and vice versa.
IV. Koolodo can be used in a sentence only if Lovitoo is also used.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
The primitive tribes-folk of the island of Lexicophobos have recently developed a language for themselves, which has a very limited vocabulary. In fact, the words can be classified into only three types : the Bingoes, the Cingoes and the Dingoes.
The Bingoes type of words are : Grumbs, Harrumphs, Ihavitoo
The Cingoes type of words are : Ihavitoo, Jingongo, Koolodo
The Dingoes type of words are : Lovitoo, Metoo, Nana
They have also devised some rules of grammar :
I. Every sentence must have only five words
II. Every sentence must have two Bingoes, one Cingo and two Dingoes.
III. If Grumbs is used in a sentence, Ihavitoo must also be used and vice versa.
IV. Koolodo can be used in a sentence only if Lovitoo is also used.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
The primitive tribes-folk of the island of Lexicophobos have recently developed a language for themselves, which has a very limited vocabulary. In fact, the words can be classified into only three types : the Bingoes, the Cingoes and the Dingoes.
The Bingoes type of words are : Grumbs, Harrumphs, Ihavitoo
The Cingoes type of words are : Ihavitoo, Jingongo, Koolodo
The Dingoes type of words are : Lovitoo, Metoo, Nana
They have also devised some rules of grammar :
I. Every sentence must have only five words
II. Every sentence must have two Bingoes, one Cingo and two Dingoes.
III. If Grumbs is used in a sentence, Ihavitoo must also be used and vice versa.
IV. Koolodo can be used in a sentence only if Lovitoo is also used.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
The primitive tribes-folk of the island of Lexicophobos have recently developed a language for themselves, which has a very limited vocabulary. In fact, the words can be classified into only three types : the Bingoes, the Cingoes and the Dingoes.
The Bingoes type of words are : Grumbs, Harrumphs, Ihavitoo
The Cingoes type of words are : Ihavitoo, Jingongo, Koolodo
The Dingoes type of words are : Lovitoo, Metoo, Nana
They have also devised some rules of grammar :
I. Every sentence must have only five words
II. Every sentence must have two Bingoes, one Cingo and two Dingoes.
III. If Grumbs is used in a sentence, Ihavitoo must also be used and vice versa.
IV. Koolodo can be used in a sentence only if Lovitoo is also used.
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Bankatlal works x hours a day and rests y hours a day. This pattern continues for 1 week, with an exactly opposite pattern next week, and so on for four weeks. Every fifth week he has a different pattern. When he works longer than he rests, his wage per hour is twice what he earns per hour when he rests longer than he works.
The following are his daily working hours for the weeks numbered 1 to 13

A week consist of six days and a month consists of 4 weeks
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Bankatlal works x hours a day and rests y hours a day. This pattern continues for 1 week, with an exactly opposite pattern next week, and so on for four weeks. Every fifth week he has a different pattern. When he works longer than he rests, his wage per hour is twice what he earns per hour when he rests longer than he works.
The following are his daily working hours for the weeks numbered 1 to 13

A week consist of six days and a month consists of 4 weeks
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Bankatlal works x hours a day and rests y hours a day. This pattern continues for 1 week, with an exactly opposite pattern next week, and so on for four weeks. Every fifth week he has a different pattern. When he works longer than he rests, his wage per hour is twice what he earns per hour when he rests longer than he works.
The following are his daily working hours for the weeks numbered 1 to 13

A week consist of six days and a month consists of 4 weeks
CAT/1994(DILR)
Question. 355
The new manager Khushaldas stipulated that Rs 5 be deducted for every hour of rest and Rs 25 be paid per hour starting 9th week, then what will be the change in Bankatlal’s salary for the 3rd month? (Hourly deductions and salaries are constant for all weeks starting 9th week)
Comprehension
Directions for Questions: Study the information below and answer questions based on it.
Bankatlal works x hours a day and rests y hours a day. This pattern continues for 1 week, with an exactly opposite pattern next week, and so on for four weeks. Every fifth week he has a different pattern. When he works longer than he rests, his wage per hour is twice what he earns per hour when he rests longer than he works.
The following are his daily working hours for the weeks numbered 1 to 13

A week consist of six days and a month consists of 4 weeks