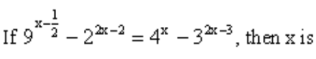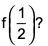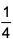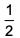CAT Quantitative Ability Questions | CAT Functions questions

CAT/2021.1(Quantitative Ability)

Question. 1

The number of integers "n" that satisfy the inequalities |n - 60| < |n - 100| < |n - 20| is

CAT/2021.1(Quantitative Ability)

Question. 2

CAT/2021.2(Quantitative Ability)

Question. 3

For a real number "x" the condition | 3x - 20 | + | 3x - 40 | = 20 necessarily holds if

CAT/2021.2(Quantitative Ability)

Question. 4

For all real values of x, the range of the function f(x) = (x²+2x+4)/(2x²+4x+9) is

CAT/2021.2(Quantitative Ability)

Question. 5

Consider the pair of equations: x² - xy - x = 22 and y² - xy + y = 34. If x>y, then x-y equals

CAT/2021.3(Quantitative Ability)

Question. 6

CAT/2021.3(Quantitative Ability)

Question. 7

If f(x) = x² - 7x and g(x) = x+3, then the minimum value of f(g(x)) - 3x is

CAT/2020.1(Quantitative Ability)

Question. 8

If f(5 + x) = f(5 - x) for every real x and f(x) = 0 has four distinct real roots, then the sum of the roots is

CAT/2020.2(Quantitative Ability)

Question. 9

Let f(x) = x² + ax + b and g(x) = f(x + 1) - f(x - 1). If f(x) ≥ 0 for all real x, and g(20) = 72, then the smallest possible value of b is

CAT/2020.3(Quantitative Ability)

Question. 10

If f(x+y) = f(x)f(y) and f(5) = 4, then f(10) - f(-10) is equal to

CAT/2019.1(Quantitative Ability)

Question. 11

For any positive integer n, let f(n) = n(n + 1) if n is even, and f(n) = n + 3 if n is odd. If m is a positive integer such that 8f(m + 1) - f(m) = 2, then m equals

CAT/2019.1(Quantitative Ability)

Question. 12

Consider a function f(x+y) = f(x) f(y) where x , y are positive integers, and f(1) = 2. If f (a+1) + f (a+2) + ..... + f(a+n) = 16 (2ⁿ - 1) then a is equal to.

CAT/2019.2(Quantitative Ability)

Question. 13

Let f be a function such that f (mn) = f (m) f (n) for every positive integers m and n. If f (1), f (2) and f (3) are positive integers, f (1) < f (2), and f (24) = 54, then f (18) equals

CAT/2018.1(Quantitative Ability)

Question. 14

If f(x + 2) = f(x) + f(x + 1) for all positive integers x, and f(11) = 91, f(15) = 617, then f(10) equals

CAT/2018.1(Quantitative Ability)

Question. 15

Let f(x)=min{2x², 52 - 5x}, where x is any positive real number.Then the maximum possible value of f(x) is [TITA]

CAT/2018.2(Quantitative Ability)

Question. 16

Let f(x)=max{5x, 52 - 2x²}, where x is any positive real number.Then the minimum possible value of f(x) is 

CAT/2017.1(Quantitative Ability)

Question. 17

Suppose, log₃x = log₁₂y = a, where x, y are positive numbers. If G is the geometric mean of x and y, and log₆G is equal to

CAT/2017.1(Quantitative Ability)

Question. 18

If f₁(x) = x² + 11x + n and f₂(x) = x, then the largest positive integer n for which the equation f₁(x) = f₂(x) has two distinct real roots, is

CAT/2017.1(Quantitative Ability)

Question. 19

CAT/2017.2(Quantitative Ability)

Question. 20

Let f(x) = x² and g(x) = 2^x, for all real x. Then the value of f( f(g(x))  +  g(f(x)) ) at x = 1 is 

CAT/2017.2(Quantitative Ability)

Question. 21

The minimum possible value of the sum of the squares of the roots of the equation x² + (a + 3)x - (a + 5) = 0 is

CAT/2017.2(Quantitative Ability)

Question. 22

CAT/2017.2(Quantitative Ability)

Question. 23

If f(ab) = f(a)f(b) for all positive integers a and b, then the largest possible value of f(1) is

CAT/2017.2(Quantitative Ability)

Question. 24

Let f(x) = 2x – 5 and g(x) = 7 – 2x. Then |f(x) + g(x)| = |f(x)| + |g(x)| if and only if

CAT/2008(Quantitative Ability)

Question. 25

Let f(x) be a function satisfying f(x)f(y) f(xy) = for all real x, y. If f(2) = 4, then what is the value of

 

CAT/2008(Quantitative Ability)

Question. 26

Suppose, the seed of any positive integer n is defined as follows:

seed(n) = n, if n < 10

            = seed(s(n)), otherwise,

where s(n) indicates the sum of digits of n.

For example, seed(7) = 7, seed(248) = seed(2 + 4 + 8) = seed(14) = seed(1 + 4) = seed(5) = 5 etc.

How many positive integers n, such that n < 500, will have seed (n) = 9?

CAT/2007(Quantitative Ability)

Question. 27

A function ƒ(x) satisfies ƒ(1) = 3600 and ƒ(1) + ƒ(2) + ... + ƒ(n) = n² f(n), for all positive integers n > 1. What is the value of ƒ(9)?

CAT/2005(Quantitative Ability)

Question. 28

Let g(x) be a function such that g(x + 1) + g(x – 1) = g(x) for every real x. Then for what value of p is the relation g(x + p) = g(x) necessarily true for every real x?

CAT/2004(Quantitative Ability)

Question. 29

On January 1, 2004 two new societies, S1 and S2 , are formed, each with n members. On the first day of each subsequent month, S1 adds b members while S2 multiplies its current number of members by a constant factor r. Both the societies have the same number of members on July 2, 2004. If b = 10.5n, what is the value of r?

CAT/2004(Quantitative Ability)

Question. 30

If f (x) = x³ – 4x + p, and f (0) and f (1) are of opposite signs, then which of the following is necessarily true?

CAT/2004(Quantitative Ability)

Question. 31

Let f (x) = ax² – b | x |, where a and b are constants. Then at x = 0, f (x) is

CAT/2004(Quantitative Ability)

Question. 32

CAT/2004(Quantitative Ability)

Question. 33

Which of the following is necessarily true?

CAT/2003(Quantitative Ability)

Question. 34

Let g (x) = max (5–x, x + 2). The smallest possible value of g (x) is

CAT/2003(Quantitative Ability)

Question. 35

CAT/2003(Quantitative Ability)

Question. 36

When the curves y = log₁₀ x and y = x^–1 are drawn in the x-y plane, how many times do they intersect for values x ≥ 1 ?

CAT/2003(Quantitative Ability)

Question. 37

Consider the following two curves in the x-y plane; y = x³ + x² + 5; y = x² + x + 5

Which of the following statements is true for -2 ≤ x ≤ 2 ?

CAT/2002(Quantitative Ability)

Question. 38

CAT/2002(Quantitative Ability)

Question. 39

Suppose, for any real number x, [x] denotes the greatest integer less than or equal to x. Let L (x, y) = [x] + [y] + [x + y] and R(x,y)= [2x] + [2y]. Then it’s impossible to find any two positive real numbers x and y for which

CAT/2002(Quantitative Ability)

Question. 40

Functions m and M are defined as follows:

m(a, b, c) = min (a + b, c, a)

M(a, b, c) = max (a + b, c, a)

If a = – 2, b = – 3 and c = 2 what is the maximum between [m(a,b,c) M(a,b,c)]/ 2 + and [m(a,b,c) M(a,b,c)]/2 ?

CAT/2002(Quantitative Ability)

Question. 41

Functions m and M are defined as follows:

m(a, b, c) = min (a + b, c, a)

M(a, b, c) = max (a + b, c, a)

 If a and b, c are negative, then what gives the minimum of a and b?

CAT/2002(Quantitative Ability)

Question. 42

Functions m and M are defined as follows:

m(a, b, c) = min (a + b, c, a)

M(a, b, c) = max (a + b, c, a)

What is m (M(a–b, b,c), m (a + b,c,b) , –M (a,b,c)) for a = 2, b= 4, c = 3?

CAT/2000(Quantitative Ability)

Question. 43

Certain relation is defined among variable A & B.

Using the relation answer the questions given below :

@ (A, B) = average of A and B

\ (A, B) = product of A and B

x (A, B) = the result when A is divided by B

The sum of A and B is given by

CAT/2000(Quantitative Ability)

Question. 44

Certain relation is defined among variable A & B.

Using the relation answer the questions given below :

@ (A, B) = average of A and B

\ (A, B) = product of A and B

x (A, B) = the result when A is divided by B

The average of A, B and C is given by

CAT/2000(Quantitative Ability)

Question. 45

CAT/2000(Quantitative Ability)

Question. 46

Which of the following is necessarily false ?

CAT/2000(Quantitative Ability)

Question. 47

 If f (x, y) = g (x, y) then

CAT/2000(Quantitative Ability)

Question. 48

Which of the following equations will best fit for the given data ?

CAT/2000(Quantitative Ability)

Question. 49

If f(0, y) y 1, and f (x 1, y) f (x,f (x, y)) = + += then, what is the value of f (1, 2) ?

CAT/2000(Quantitative Ability)

Question. 50

Graphs of some functions are given. Mark the correct options from the following:

CAT/2000(Quantitative Ability)

Question. 51

Graphs of some functions are given. Mark the correct options from the following:

CAT/2000(Quantitative Ability)

Question. 52

Graphs of some functions are given. Mark the correct options from the following:

CAT/2000(Quantitative Ability)

Question. 53

CAT/2000(Quantitative Ability)

Question. 54

If x = –1 what will f⁵ (x) be

CAT/1999(Quantitative Ability)

Question. 55

If x & y are real numbers, the functions are defined as f (x, y) = | x + y |,F (x, y) = –f (x, y) and G (x, y) = –F (x, y) . Now with the help of this information answer the following questions.

Which of the following will be necessarily true?

CAT/1999(Quantitative Ability)

Question. 56

If x & y are real numbers, the functions are defined as f (x, y) = | x + y |,F (x, y) = –f (x, y) and G (x, y) = –F (x, y) . Now with the help of this information answer the following questions.

If y = x, which of the following will give x² as the final value ?

CAT/1999(Quantitative Ability)

Question. 57

If x & y are real numbers, the functions are defined as f (x, y) = | x + y |,F (x, y) = –f (x, y) and G (x, y) = –F (x, y) . Now with the help of this information answer the following questions.

What will be the final value given by the function G (f (G (F (f (2, –3),0) – 2),0), -1)?

CAT/1999(Quantitative Ability)

Question. 58

Any function has been defined for a variable x, where range of x (–2,2).

CAT/1999(Quantitative Ability)

Question. 59

Any function has been defined for a variable x, where range of x (–2,2).

CAT/1999(Quantitative Ability)

Question. 60

Any function has been defined for a variable x, where range of x (–2,2).

CAT/1999(Quantitative Ability)

Question. 61

Any function has been defined for a variable x, where range of x (–2,2).

CAT/1999(Quantitative Ability)

Question. 62

There is a set of 'n' natural numbers. The function 'H' is such that it finds the highest common factor between any two numbers. What is the minimum number of times that the function has to be invoked to find the H.C.F. of the given set of numbers?

CAT/1998(Quantitative Ability)

Question. 63

The following operations are defined for real numbers a # b = a + b if a and b both are positive else a # b = 1. a ∇ b = (ab)^a+b if ab is positive else a ∇ b = 1.

(2 # 1)/(1 ∇ 2) = 

CAT/1998(Quantitative Ability)

Question. 64

The following operations are defined for real numbers a # b = a + b if a and b both are positive else a # b = 1. a ∇ b = (ab)^a+b if ab is positive else a ∇ b = 1.

CAT/1998(Quantitative Ability)

Question. 65

The following operations are defined for real numbers a # b = a + b if a and b both are positive else a # b = 1. a ∇ b = (ab)^a+b if ab is positive else a ∇ b = 1.

((X # – Y)/(– X ∇ Y)) = 3/8, then which of the following must be true?

CAT/1997(Quantitative Ability)

Question. 66

The following functions have been defined :

la (x, y, z) = min (x + y, y + z)

le (x, y, z) = max (x – y, y – z)

ma (x, y, z) = (½) [le (x, y, z) + la (x, y, z)]

Given that x > y > z > 0, which of the following is necessarily true?

CAT/1997(Quantitative Ability)

Question. 67

The following functions have been defined :

la (x, y, z) = min (x + y, y + z)

le (x, y, z) = max (x – y, y – z)

ma (x, y, z) = (½) [le (x, y, z) + la (x, y, z)]

What is the value of ma (10, 4, le (la (10, 5, 3), 5, 3)) ?

CAT/1997(Quantitative Ability)

Question. 68

The following functions have been defined :

la (x, y, z) = min (x + y, y + z)

le (x, y, z) = max (x – y, y – z)

ma (x, y, z) = (½) [le (x, y, z) + la (x, y, z)]

For x = 15, y = 10 and z = 9, find the value of : le (x, min (y, x – z), le (9, 8, ma (x, y, z)))

CAT/1996(Quantitative Ability)

Question. 69

A,S, M and D are functions of x and y, and they are defined as follows :

A (x, y) = x + y

S (x, y) = x – y

M (x, y) = xy

D (x, y) = x / y

where y ≠ 0.

What is the value of M(M(A(M(x, y), S (y, x)), x), A (y,x)) for x =2 , y = 3 ?

CAT/1996(Quantitative Ability)

Question. 70

A,S, M and D are functions of x and y, and they are defined as follows :

A (x, y) = x + y

S (x, y) = x – y

M (x, y) = xy

D (x, y) = x / y

where y ≠ 0.

What is the value of S[M(D(A(a, b),2), D(A(a, b),2)),M(D(S(a,b),2), D(S(a, b), 2))] ?

CAT/1995(Quantitative Ability)

Question. 71

le (x, y) = least of (x, y)

mo (x) = |x|

me (x, y) = maximum of (x, y)

Find the value of me (a mo(le (a,b)), mo (a me (mo (a) mo (b)))), + + at a = –2 and b = –3.

CAT/1995(Quantitative Ability)

Question. 72

le (x, y) = least of (x, y)

mo (x) = |x|

me (x, y) = maximum of (x, y)

 Which of the following must always be correct for a, b > 0

CAT/1995(Quantitative Ability)

Question. 73

le (x, y) = least of (x, y)

mo (x) = |x|

me (x, y) = maximum of (x, y)

 For what values of a is me (a² -  3a, a - 3) < 0?

CAT/1995(Quantitative Ability)

Question. 74

le (x, y) = least of (x, y)

mo (x) = |x|

me (x, y) = maximum of (x, y)

For what values of a le (a² – 3a, a – 3) < 0 ?

CAT/1995(Quantitative Ability)

Question. 75

Largest value of min (2 + x², 6 – 3x), when x > 0 is

CAT/1994(Quantitative Ability)

Question. 76

If md (x) = | x |,

mn (x, y) = minimum of x and y and

Ma (a, b, c, ....) = maximum of a, b, c, ...

Value of Ma [md (a), mn (md(b), a), mn (ab, md(ac))] where a = –2, b = –3, c = 4 is

CAT/1994(Quantitative Ability)

Question. 77

If md (x) = | x |,

mn (x, y) = minimum of x and y and

Ma (a, b, c, ....) = maximum of a, b, c, ....

Given that a > b then the relation Ma [md (a), mn (a, b)] = mn [a, md (Ma (a, b))] does not hold if

CAT/1994(Quantitative Ability)

Question. 78

fog (x) =

CAT/1994(Quantitative Ability)

Question. 79

For what value of x; f (x) = g (x – 3) ?

CAT/1994(Quantitative Ability)

Question. 80

What is value of (gofofogogof )(x)(fogofog)(x) ?

CAT/1994(Quantitative Ability)

Question. 81

What is the value of fo(fog) o (gof) (x)?