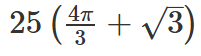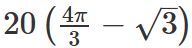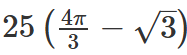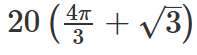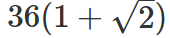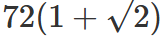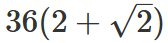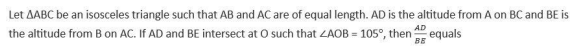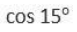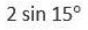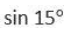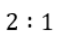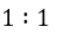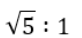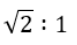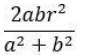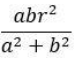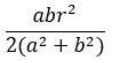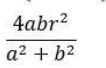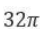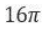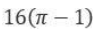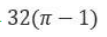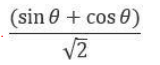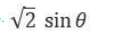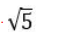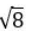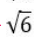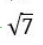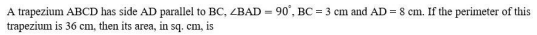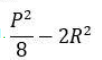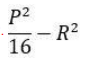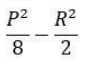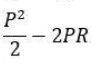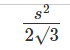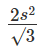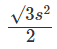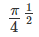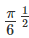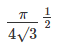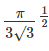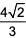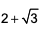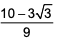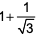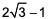CAT Quantitative Ability Questions | CAT Geometry questions
CAT Geometry Questions | CAT Past Year Questions| Basic Concepts in Geometry; Classification of Triangles; Quadrilateral; Co- ordinate Geometry; Equations of Parallel and Perpendicular Lines; Bisectors of Angles between two lines; Concurrence of Straight Lines; General Equation of Circles; Position of point with respect to a Circle.CAT/2024.3(Quantitative Ability)
Question. 2
The midpoints of sides AB, BC, and AC in △ ABC are M, N, and P, respectively. The medians drawn from A, B, and C intersect the line segments MP, MN and NP at X, Y, and Z, respectively. If the area of △ ABC is 1440 sq cm, then the area, in sq cm, of △ XYZ is
90
CAT/2023.3(Quantitative Ability)
Question. 10
In a regular polygon, any interior angle exceeds the exterior angle by 120 degrees. Then, the number of diagonals of this polygon is
54
45
CAT/2023.1(Quantitative Ability)
Question. 16
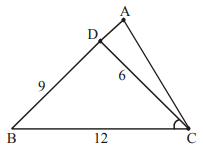
In a right-angled triangle ∆ABC, the altitude AB is 5 cm, and the base BC is 12 cm. P and Q are two points on BC such that the areas of ∆ABP, ∆ABQ and ∆ABC are in arithmetic progression. If the area of ∆ABC is 1.5 times the area of ∆ABP, the length of PQ, in cm, is
10
66
CAT/2020.2(Quantitative Ability)
Question. 33
Let C1 and C2 be concentric circles such that the diameter of C1 is 2cm longer than that of C2. If a chord of C1 has length 6 cm and is a tangent to C2, then the diameter, in cm of C1 is
10
CAT/2020.3(Quantitative Ability)
Question. 36
In a trapezium ABCD, AB is parallel to DC, BC is perpendicular to DC and ∠BAD = 45°. If DC = 5 cm, BC = 4 cm, the area of the trapezium in sq. cm is
28
CAT/2019.1(Quantitative Ability)
Question. 38
With rectangular axes of coordinates, the number of paths from (1,1) to (8,10) via (4,6), where each step from any point (x,y) is either to (x,y+1) or to (x+1,y) is
3920
CAT/2019.2(Quantitative Ability)
Question. 45
Let A and B be two regular polygons having a and b sides, respectively. If b = 2a and each interior angle of B is 3/2 times each interior angle of A, then each interior angle, in degrees, of a regular polygon with a + b sides is
150
CAT/2018.1(Quantitative Ability)
Question. 47
In a circle with centre O and radius 1 cm, an arc AB makes an angle 60 degrees at O. Let R be the region bounded by the radii OA, OB and the arc AB. If C and D are two points on OA and OB, respectively, such that OC = OD and the area of triangle OCD is half that of R, then the length of OC, in cm, is
CAT/2018.1(Quantitative Ability)
Question. 48
Given an equilateral triangle T1 with side 24 cm, a second triangle T2 is formed by joining the midpoints of the sides of T1. Then a third triangle T3 is formed by joining the midpoints of the sides of T2. If this process of forming triangles is continued, the sum of the areas, in sq cm, of infinitely many such triangles T1, T2, T3,... will be
CAT/2018.2(Quantitative Ability)
Question. 52
On a triangle ABC, a circle with diameter BC is drawn, intersecting AB and AC at points P and Q, respectively. If the lengths of AB, AC, and CP are 30 cm, 25 cm, and 20 cm respectively, then the length of BQ, in cm, is
24
CAT/2017.1(Quantitative Ability)
Question. 57
Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq. cm, of the region enclosed by BPC and BQC is:
CAT/2017.1(Quantitative Ability)
Question. 58
Let ABC be a right-angled triangle with BC as the hypotenuse. Lengths of AB and AC are 15 km and 20 km, respectively. The minimum possible time, in minutes, required to reach the hypotenuse from A at a speed of 30 km per hour is
24
CAT/2017.1(Quantitative Ability)
Question. 59
Let AB, CD, EF, GH, and JK be five diameters of a circle with center at O. In how many ways can three points be chosen out of A, B, C, D, E, F, G, H, J, K, and O so as to form a triangle?
160
CAT/2017.2(Quantitative Ability)
Question. 62
The base of a vertical pillar with uniform cross section is a trapezium whose parallel sides are of lengths 10 cm and 20 cm while the other two sides are of equal length. The perpendicular distance between the parallel sides of the trapezium is 12 cm. If the height of the pillar is 20 cm, then the total area, in sq cm, of all six surfaces of the pillar is
CAT/2017.2(Quantitative Ability)
Question. 64
ABCD is a quadrilateral inscribed in a circle with centre O. If ∠COD = 120 degrees and ∠BAC = 30 degrees, then the value of ∠BCD (in degrees) is
90
CAT/2017.2(Quantitative Ability)
Question. 65
If three sides of a rectangular park have a total length 400 ft., then the area of the park is maximum when the length (in ft.) of its longer side is
200
CAT/2017.2(Quantitative Ability)
Question. 66
Let P be an interior point of a right-angled isosceles triangle ABC with hypotenuse AB. If the perpendicular distance of P from each of AB, BC, and CA is 4(√2 - 1) cm, then the area, in sq. cm, of the triangle ABC is
16
CAT/2008(Quantitative Ability)
Question. 67
In a triangle ABC, the lengths of the sides AB and AC equal 17.5 cm and 9 cm respectively. Let D be a point on the line segment BC such that AD is perpendicular to BC. If AD = 3 cm, then what is the radius (in cm) of the circle circumscribing the triangle ABC?
CAT/2008(Quantitative Ability)
Question. 69
Consider a square ABCD with midpoints E, F, G, H of AB, BC, CD and DA respectively. Let L denote the line passing through F and H. Consider points P and Q, on L and inside ABCD, such that the angles APD and BQC both equal 120°. What is the ratio of the area of ABQCDP to the remaining area inside ABCD?
CAT/2005(Quantitative Ability)
Question. 72
In the following figure, the diameter of the circle is 3 cm. AB and MN are two diameters such that MN is perpendicular to AB. In addition, CG is perpendicular to AB such that AE : EB = 1 : 2, and DF is perpendicular to MN such that NL : LM = 1 : 2. The length of DH in cm is
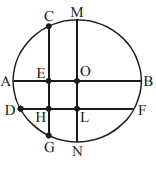
CAT/2005(Quantitative Ability)
Question. 75
Consider a triangle drawn on the X-Y plane with its three vertices at (41, 0), (0, 41) and (0, 0), each vertex being represented by its (X, Y) coordinates. The number of points with integer coordinates inside the triangle (excluding all the points on the boundary) is
CAT/2004(Quantitative Ability)
Question. 76
A father and his son are waiting at a bus stop in the evening. There is a lamp post behind them. The lamp post, the father and his son stand on the same straight line. The father observes that the shadows of his head and his son’s head are incident at the same point on the ground. If the heights of the lamp post , the father and his son are 6 metres, 1.8 metres and 0.9 metres respectively, and the father is standing 2.1 metres away from the post, then how far (in meters) is the son standing from his father?
Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
In the adjoining figure, I and II are circles with centers P and Q respectively. The two circle touch each other and have a common tangent that touches them at points R and S respectively. This common tangent meets the line joining P and Q at O. The diameters of I and II are in the rartio 4 : 3. It is also known that the length of PO is 28 cm.

Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
In the adjoining figure, I and II are circles with centers P and Q respectively. The two circle touch each other and have a common tangent that touches them at points R and S respectively. This common tangent meets the line joining P and Q at O. The diameters of I and II are in the rartio 4 : 3. It is also known that the length of PO is 28 cm.

Comprehension
Directions for Questions: Answer the questions on the basis of the information given below.
In the adjoining figure, I and II are circles with centers P and Q respectively. The two circle touch each other and have a common tangent that touches them at points R and S respectively. This common tangent meets the line joining P and Q at O. The diameters of I and II are in the rartio 4 : 3. It is also known that the length of PO is 28 cm.

CAT/2003(Quantitative Ability)
Question. 84
Each side of a given polygon is parallel to either the X or the Y axis. A corner of such a polygon is said to be convex if the internal angle is 90° or concave if the internal angle is 270°. If the number of convex corners in such a polygon is 25, the number of concave corners must be
CAT/2000(Quantitative Ability)
Question. 100
There is a regular octagon A B C D E F G H, a frog is at the vertex A. It can jump on to any of the vertices except the exactly opposite vertex. The frog visits all the vertices exactly once and then reaches vertex E then how many times did it jump before reaching E?
CAT/1999(Quantitative Ability)
Question. 104
The figure below shows two concentric circles with centre O. PQRS is a square inscribed in the outer circle. It also circumscribes the inner circle, touching it at point B, C, D and A. What is the ratio of the perimeter of the outer circle to that of polygon ABCD?

CAT/1995(Quantitative Ability)
Question. 114
The length of a ladder is exactly equal to the height of the wall it is resting against. If lower end of the ladder is kept on a stool of height 3 m and the stool is kept 9 m away from the wall the upper end of the ladder coincides with the tip of the wall. Then, the height of the wall is