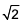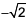CAT Quantitative Ability Questions | CAT Permutation, Combination and Probability questions
Permutation, Combination and Probability | PnC And Probability for CAT | CAT Past Year PNC Questions| Fundamental Principle of Counting; Distinguishable Permutations; Combination; Difference between Permutation and Combination; Counting Formulae for Combination; Division and Distribution of Objects; Random Experiments; Event; Probability of at least one of the n Independent Events; Baye’s Formula; Total Probability Theorem.CAT/2022.1(Quantitative Ability)
Question. 1
The number of ways of distributing 20 identical balloons among 4 children such that each child gets some balloons but no child gets an odd number of balloons, is
84
CAT/2021.1(Quantitative Ability)
Question. 2
The number of groups of three or more distinct numbers that can be chosen from 1, 2, 3, 4, 5, 6, 7, and 8 so that the groups always include 3 and 5, while 7 and 8 are never included together is
47
CAT/2021.2(Quantitative Ability)
Question. 3
A box has 450 balls, each either white or black, there being as many metallic white balls as metallic black balls. If 40% of the white balls and 50% of the black balls are metallic, then the number of non-metallic balls in the box is
250
CAT/2021.2(Quantitative Ability)
Question. 4
The number of ways of distributing 15 identical balloons, 6 identical pencils and 3 identical erasers among 3 children, such that each child gets at least four balloons and one pencil, is
1000
CAT/2020.3(Quantitative Ability)
Question. 5
How many integers in the set {100, 101, 102, ..., 999} have at least one digit repeated?
252
CAT/2018.2(Quantitative Ability)
Question. 6
In a tournament, there are 43 junior level and 51 senior level participants. Each pair of juniors play one match. Each pair of seniors play one match. There is no junior versus senior match. The number of girl versus girl matches in junior level is 153, while the number of boy versus boy matches in senior level is 276. The number of matches a boy plays against a girl is
1098
CAT/2017.2(Quantitative Ability)
Question. 9
How many four digit numbers, which are divisible by 6, can be formed using the digits 0, 2, 3, 4, 6, such that no digit is used more than once and 0 does not occur in the left-most position?
50
Comprehension
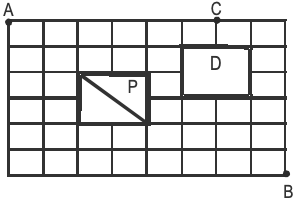
The figure below shows the plan of a town. The streets are at right angles to each other. A rectangular park (P) is situated inside the town with a diagonal road running through it. There is also a prohibited region (D) in the town.
Comprehension
The figure below shows the plan of a town. The streets are at right angles to each other. A rectangular park (P) is situated inside the town with a diagonal road running through it. There is also a prohibited region (D) in the town.

CAT/2005(Quantitative Ability)
Question. 16
Three Englishmen and three Frenchmen work for the same company. Each of them knows a secret not known to others. Theyneed to exchange these secrets over person-to-person phone calls so that eventually each person knows all six secrets. None ofthe Frenchmen knows English, and only one Englishman knows French. What is the minimum number of phone calls needed forthe above purpose?
CAT/2005(Quantitative Ability)
Question. 20
In a chess competition involving some boys and girls of a school, every student had to play exactly one game with every other student. It was found that in 45 games both the players were girls, and in 190 games both were boys. The number of games in which one player was a boy and the other was a girl is
CAT/2004(Quantitative Ability)
Question. 24
Each family in a locality has at most two adults, and no family has fewer than 3 children. Considering all the families together, thereare more adults than boys, more boys than girls, and more girls than families. Then the minimum possible number of families inthe locality is
CAT/2003(Quantitative Ability)
Question. 27
Twenty-seven persons attend a party. Which one of the following statements can never be true?
CAT/2003(Quantitative Ability)
Question. 29
There are 6 boxes numbered 1,2,.........6. Each box is to be filled up either with a red or a green ball in such a way that at least 1 boxcontains a green ball and the boxes containing green balls are consecutively numbered. The total number of ways in which thiscan be done is
CAT/2003(Quantitative Ability)
Question. 30
A graph may be defined as a set of points connected by lines called edges. Every edge connects a pair of points. Thus, a triangleis a graph with 3 edges and 3 points. The degree of a point is the number of edges connected to it. For example, a triangle is agraph with three points of degree 2 each. Consider a graph with 12 points. It is possible to reach any point from any other pointthrough a sequence of edges. The number of edges, e, in the graph must satisfy the condition
Comprehension
Directions for questions: Read the information given below and answer the questions that follow :
A string of three English letters is formed as per the following rules :
(a) The first letter is any vowel.
(b) The second letter is m, n or p
(c) If the second letter is m then the third letter is any vowel which is different from the first letter
(d) If the second letter is n then the third letter is e or u.
(e) If second letter is p then the third letter is the same as the first letter
Comprehension
Directions for questions: Read the information given below and answer the questions that follow :
A string of three English letters is formed as per the following rules :
(a) The first letter is any vowel.
(b) The second letter is m, n or p
(c) If the second letter is m then the third letter is any vowel which is different from the first letter
(d) If the second letter is n then the third letter is e or u.
(e) If second letter is p then the third letter is the same as the first letter
CAT/2003(Quantitative Ability)
Question. 33
There are 12 towns grouped into four zones with three towns per zone. It is intended to connect the towns with telephone linessuch that every two towns are connected with three direct lines if they belong to the same zone, and with only one direct lineotherwise. How many direct telephone lines are required?
CAT/2003(Quantitative Ability)
Question. 34
An intelligence agency forms a code of two distinct digits selected from 0, 1, 2, ............ , 9 such that the first digit of the code isnonzero. The code, handwritten on a slip, can however potentially create confusion when read upside down –– for example, thecode 91 may appear as 16. How many codes are there for which no such confusion can arise?
Comprehension
Directions for questions: Read the information given below and answer the questions that follow :
Each of the 11 letters A, H, I, M, O, T, U, V, W, X and Z appears same when looked at in a mirror. They are called symmetric letters.Other letters in the alphabet are asymmetric letters.
Comprehension
Directions for questions: Read the information given below and answer the questions that follow :
Each of the 11 letters A, H, I, M, O, T, U, V, W, X and Z appears same when looked at in a mirror. They are called symmetric letters.Other letters in the alphabet are asymmetric letters.
CAT/2002(Quantitative Ability)
Question. 40
If there are 10 positive real numbers n1 < n2 < n3 ... < n10. How many triplets of these numbers (n1, n2, n3), (n2, n3, n4), ... can begenerated such that in each triplet the first number is always less than the second number, and the second number is always lessthan the third number?
CAT/2002(Quantitative Ability)
Question. 41
If there are 10 positive real numbers n1 < n2 < n3 ...... < n10. How many triplets of these numbers (n1, n2, n3), (n2, n3, n4), ..... canbe generated such that in each triplet the first number is always less than the second number and the second number is alwaysless than the third number?
CAT/2001(Quantitative Ability)
Question. 43
Ashish is given Rs. 158 in one rupee denominations. He has been asked to allocate them into a number of bags such that anyamount required between Re. 1 and Rs. 158 can be given by handing out a certain number of bags without opening them. Whatis the minimum number of bags required?
CAT/2000(Quantitative Ability)
Question. 46
Sameer has to make a telephone call to his friend Harish Unfortunately he does not remember the 7- digit phone number. But he remembers that the first 3 digits are 635 or 674, the number is odd and there is exactly one 9 in the number. The minimum number of trials that Sameer has to make to be successful is
CAT/2000(Quantitative Ability)
Question. 47
There are three books on table A which has to be moved to table B. The order of the book on Table A was 1, 2, 3, with book 1 at the bottom. The order of the book on table B should be with book 2 on top and book 1 on bottom. Note that you can pick up the books in the order they have been arranged. You can’t remove the books from the middle of the stack. In how many minimum steps can we place the books on table B in the required order?
Comprehension
Directions for questions: Read the information given below and answer the questions that follow :
The tournament for ABC Cup is arranged as per the following rules: in the beginning 16 teams are entered and divided in 2 groupsof 8 teams each where the team in any group plays exactly once with all the teams in the same group. At the end of this round topfour teams from each group advance to the next round in which two teams play each other and the losing team goes out of thetournament. The rules of the tournament are such that every match can result only in a win or a loss and not in a tie. The winnerin the first round takes one point from the win and the loser gets zero. In case of tie on a position the rules are very complex andinclude a series of deciding measures.
Comprehension
Directions for questions: Read the information given below and answer the questions that follow :
The tournament for ABC Cup is arranged as per the following rules: in the beginning 16 teams are entered and divided in 2 groupsof 8 teams each where the team in any group plays exactly once with all the teams in the same group. At the end of this round topfour teams from each group advance to the next round in which two teams play each other and the losing team goes out of thetournament. The rules of the tournament are such that every match can result only in a win or a loss and not in a tie. The winnerin the first round takes one point from the win and the loser gets zero. In case of tie on a position the rules are very complex andinclude a series of deciding measures.
Comprehension
Directions for questions: Read the information given below and answer the questions that follow :
The tournament for ABC Cup is arranged as per the following rules: in the beginning 16 teams are entered and divided in 2 groupsof 8 teams each where the team in any group plays exactly once with all the teams in the same group. At the end of this round topfour teams from each group advance to the next round in which two teams play each other and the losing team goes out of thetournament. The rules of the tournament are such that every match can result only in a win or a loss and not in a tie. The winnerin the first round takes one point from the win and the loser gets zero. In case of tie on a position the rules are very complex andinclude a series of deciding measures.
Comprehension
Directions for questions: Read the information given below and answer the questions that follow :
The tournament for ABC Cup is arranged as per the following rules: in the beginning 16 teams are entered and divided in 2 groupsof 8 teams each where the team in any group plays exactly once with all the teams in the same group. At the end of this round topfour teams from each group advance to the next round in which two teams play each other and the losing team goes out of thetournament. The rules of the tournament are such that every match can result only in a win or a loss and not in a tie. The winnerin the first round takes one point from the win and the loser gets zero. In case of tie on a position the rules are very complex andinclude a series of deciding measures.
CAT/1999(Quantitative Ability)
Question. 55
Five persons A, B, C, D and E along with their wives are seated around a round table such that no two men are adjacent to each other. The wives are three places away from their husbands. Mrs. C is on the left of Mr. A, Mrs. E is two places to the right of Mrs. B. Then, who is on the right hand side of Mr. A?
CAT/1998(Quantitative Ability)
Question. 61
A, B, C, D, ..................X, Y, Z are the players who participated in a tournament. Everyone played with every other player exactly once. A win scores 2 points, a draw scores 1 point and a loss scores 0 points. None of the matches ended in a draw. No two players scored the same score. At the end of the tournament, the ranking list is published which is in accordance with the alphabetical order. Then
CAT/1995(Quantitative Ability)
Question. 66
Boxes numbered 1, 2, 3, 4 and 5 are kept in a row and they are to be filled with either a red or a blue ball, such that no two adjacent boxes can be filled with blue balls. Then how many different arrangements are possible, given that all balls of a given colour are exactly identical in all respects?