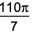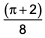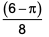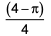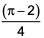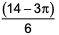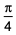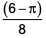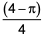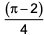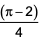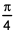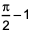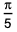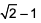CAT Quantitative Ability Questions | CAT Mensuration questions

CAT/2021.1(Quantitative Ability)

Question. 1

If the area of a regular hexagon is equal to the area of an equilateral triangle of side 12 cm, then the length, in cm, of each side of the hexagon is

CAT/2021.1(Quantitative Ability)

Question. 2

A circle of diameter 8 inches is inscribed in a triangle ABC where ∠ABC = 90. If BC= 10 inches, then the area of the triangle in square inches is

CAT/2021.2(Quantitative Ability)

Question. 3

If a rhombus has area 12 sq cm and side length 5 cm, then the length, in cm, of its longer diagonal is

CAT/2021.2(Quantitative Ability)

Question. 4

The sides AB and CD of a trapezium ABCD are parallel, with AB being the smaller side. P is the midpoint of CD and ABPD is a parallelogram. If the difference between the areas of the parallelogram ABPD and the triangle BPC is 10 sq cm, then the area, in sq cm, of the trapezium ABCD is

CAT/2021.2(Quantitative Ability)

Question. 5

Let D and E be points on sides AB and AC, respectively, of a triangle ABC, such that AD : BD = 2 : 1 and AE : CE = 2 : 3. If the area of the triangle ADE is 8 sq cm, then the area of the triangle ABC, in sq cm, is

CAT/2021.3(Quantitative Ability)

Question. 6

The cost of fencing a rectangular plot is ₹ 200 per ft along one side, and ₹ 100 per ft along the three other sides. If the area of the rectangular plot is 60000 sq. ft, then the lowest possible cost of fencing all four sides, in INR, is

CAT/2021.3(Quantitative Ability)

Question. 7

A park is shaped like a rhombus and has area 96 sq m. If 40 m of fencing is needed to enclose the park, the cost, in INR, of laying electric wires along its two diagonals, at the rate of ₹125 per m, is

CAT/2020.1(Quantitative Ability)

Question. 8

A solid right circular cone of height 27 cm is cut into 2 pieces along a plane parallel to it's base at a height of 18 cm from the base. If the difference in the volume of the two pieces is 225 cc, the volume, in cc, of the original cone is

CAT/2020.1(Quantitative Ability)

Question. 9

On a rectangular metal sheet of area 135 sq in, a circle is painted such that the circle touches opposite two sides. If the area of the sheet left unpainted is two-thirds of teh painted area tehn the perimeter of the rectangle in inches is

CAT/2020.2(Quantitative Ability)

Question. 10

The sum of perimeters of an equilateral triangle and a rectangle is 90 cm. The area, T, of the triangle and the area , R, of the rectangle, both in sq cm, satisfy the relationship R = T². If the sides of the rectangle are in the ratio 1 : 3, then the length, in cm, of the longer side of the rectangle, is

CAT/2019.1(Quantitative Ability)

Question. 11

Corners are cut off from an equilateral triangle T to produce a regular hexagon H. Then, the ratio of the area of H to the area of T is

CAT/2019.1(Quantitative Ability)

Question. 12

If the rectangular faces of a brick have their diagonals in the ratio , then the ratio of the length of the shortest edge of the brick to that of its longest edge is

CAT/2019.2(Quantitative Ability)

Question. 13

The base of a regular pyramid is a square and each of the other four sides is an equilateral triangle, length of each side being 20 cm. The vertical height of the pyramid, in cm, is

CAT/2019.2(Quantitative Ability)

Question. 14

A man makes complete use of 405 cc of iron, 783 cc of aluminium, and 351 cc of copper to make a number of solid right circular cylinders of each type of metal. These cylinders have the same volume and each of these has radius 3 cm. If the total number of cylinders is to be kept at a minimum, then the total surface area of all these cylinders, in sq cm, is

CAT/2018.1(Quantitative Ability)

Question. 15

A right circular cone, of height 12 ft, stands on its base which has diameter 8 ft. The tip of the cone is cut off with a plane which is parallel to the base and 9 ft from the base. With π = 22/7, the volume, in cubic ft, of the remaining part of the cone is

CAT/2018.1(Quantitative Ability)

Question. 16

In a parallelogram ABCD of area 72 sq cm, the sides CD and AD have lengths 9 cm and 16 cm, respectively. Let P be a point on CD such that AP is perpendicular to CD. Then the area, in sq cm, of triangle APD is

CAT/2018.2(Quantitative Ability)

Question. 17

From a rectangle ABCD of area 768 sq cm, a semicircular part with diameter AB and area 72π sq cm is removed. The perimeter of the leftover portion, in cm, is

CAT/2018.2(Quantitative Ability)

Question. 18

The area of a rectangle and the square of its perimeter are in the ratio 1 : 25. Then the lengths of the shorter and longer sides of the rectangle are in the ratio

CAT/2018.2(Quantitative Ability)

Question. 19

A parallelogram ABCD has area 48 sqcm. If the length of CD is 8 cm and that of AD is s cm, then which one of the following is necessarily true?

CAT/2017.1(Quantitative Ability)

Question. 20

A solid metallic cube is melted to form five solid cubes whose volumes are in the ratio 1 : 1 : 8: 27: 27. The percentage by which the sum of the surface areas of these five cubes exceeds the surface area of the original cube is nearest to:

CAT/2017.1(Quantitative Ability)

Question. 21

A ball of diameter 4 cm is kept on top of a hollow cylinder standing vertically. The height of the cylinder is 3 cm, while its volume is 9 π cm³. Then the vertical distance, in cm, of the topmost point of the ball from the base of the cylinder is

CAT/2008(Quantitative Ability)

Question. 22

Consider a right circular cone of base radius 4 cm and height 10 cm. A cylinder is to be placed inside the cone with one of the flat surfaces resting on the base of the cone. Find the largest possible total surface area (in sq. cm) of the cylinder.

Comprehension

Directions for Questions 7 to 10: Each question is followed by two statements A and B. Indicate your response based on the following directives.

Mark (1) if the questions can be answered using A alone but not using B alone.

Mark (2) if the question can be answered using B alone but not using A alone.

Mark (3) if the question can be answered using A and B together, but not using either A or B alone.

Mark (4) if the question cannot be answered even using A and B together.

CAT/2007(Quantitative Ability)

Question. 23

ABC Corporation is required to maintain at least 400 Kilolitres of water at all times in its factory, in order to meet safety and regulatory requirements. ABC is considering the suitability of a spherical tank with uniform wall thickness for the purpose. The outer diameter of the tank is 10 meters. Is the tank capacity adequate to met ABC’s requirements?

A: The inner diameter of the tank is at least 8 meters.

B: The tank weights 30,000 kg when empty, and is made of a material with density of 3 gm/cc.

Comprehension

Directions for Questions 7 to 10: Each question is followed by two statements A and B. Indicate your response based on the following directives.

Mark (1) if the questions can be answered using A alone but not using B alone.

Mark (2) if the question can be answered using B alone but not using A alone.

Mark (3) if the question can be answered using A and B together, but not using either A or B alone.

Mark (4) if the question cannot be answered even using A and B together.

CAT/2007(Quantitative Ability)

Question. 24

Rahim plans to draw a square JKLM with point O on the side JK but is not successful. Why is Rahim unable to draw the square?

A: The length of OM is twice that of OL.

B: The length of OM is 4 cm.

CAT/2007(Quantitative Ability)

Question. 25

Two circles with centres P and Q cut each other at two distinct points A and B. The circles have the same radii and neither P nor Q falls within the intersection of the circles. What is the smallest range that includes all possible values of the angle AQP in degrees?

Comprehension

Directions for questions 61 and 62: Answer questions on the basis of the information given below:

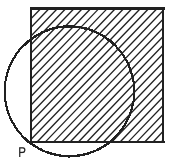
A punching machine is used to punch a circular hole of diameter two units from a square sheet of aluminium of width 2 units, as shown below. The hole is punched such that the circular hole touches one corner P of the square sheet and the diameter of the hole originating at P is in line with a diagonal of the square.

 

CAT/2006(Quantitative Ability)

Question. 26

The proportion of the sheet area that remains after punching is:

Comprehension

Directions for questions 61 and 62: Answer questions on the basis of the information given below:

A punching machine is used to punch a circular hole of diameter two units from a square sheet of aluminium of width 2 units, as shown below. The hole is punched such that the circular hole touches one corner P of the square sheet and the diameter of the hole originating at P is in line with a diagonal of the square.

 

CAT/2006(Quantitative Ability)

Question. 27

Find the area of the part of the circle (round punch) falling outside the square sheet.

CAT/2006(Quantitative Ability)

Question. 28

A semi-circle is drawn with AB as its diameter. From C, a point on AB, a line perpendicular to AB is drawn meeting the circumference of the semi-circle at D. Given that AC = 2 cm and CD = 6 cm, the area of the semi-circle (in sq. cm) will be:

CAT/2005(Quantitative Ability)

Question. 29

Two identical circles intersect so that their centres, and the points at which they intersect, form a square of side 1 cm. The area in sq. cm of the portion that is common to the two circles is

CAT/2005(Quantitative Ability)

Question. 30

A jogging park has two identical circular tracks touching each other and a rectangular track enclosing the two circles. The edges of the rectangles are tangential to the circles. Two friends, A and B, start jogging simultaneously from the point where one of the circular tracks touches the smaller side of the rectangular track. A jogs along the rectangular track, while B jogs along the two circular tracks in a figure of eight. Approximately, how much faster than A does B have to run, so that they take the same time to return to their starting point?

CAT/2005(Quantitative Ability)

Question. 31

In the X-Y plane, the area of the region bounded by the graph |x + y| + |x – y| = 4 is

CAT/2005(Quantitative Ability)

Question. 32

A rectangular floor is fully covered with square tiles of identical size. The tiles on the edges are white and the tiles in the interior are red. The number of the white tiles is the same as the number of red tiles. A possible value of the number of tiles along one edge of the floor is :

CAT/2005(Quantitative Ability)

Question. 33

Four points A, B, C and D lie on a straight line in the X-Y plane, such that AB = BC = CD and the length of AB is 1 meter. An ant at A wants to reach a sugar particle at D. But there are insect repellents kept at points B and C. The ant would not go within one meter of any insect repellent. The minimum distance in meters the ant must traverse to reach the sugar particle is

CAT/2005(Quantitative Ability)

Question. 34

Rectangular tiles each of size 70 cm by 30 cm must be laid horizontally on a rectangular floor of size 110 cm by 130 cm, such that the tiles do not overlap. A tile can be placed in any orientation so long as its edges are parallel to the edges of the floor. No tile should overshoot any edge of the floor. The maximum number of tiles that can be accommodated on the floor is

CAT/2005(Quantitative Ability)

Question. 35

Two identical circles intersect so that their centers, and the points at which they intersect, form a square of side 1 cm. The area in sq. cm of the portion that is common to the two circles is

CAT/2004(Quantitative Ability)

Question. 36

A rectangular sheet of paper, when halved by folding it at mid-point of its longer side, results in a rectangle, whose longer and shorter sides are in the same proportion as the longer and shorter sides of the original rectangle. If the shorter side of the original rectangle is 2, what is the area of the smaller rectangle?

CAT/2004(Quantitative Ability)

Question. 37

Let C be a circle with center P0 and AB be a diameter of C. Suppose P1 is the mid-point of the line segment P0 B, P2 is the mid-point of the line segment P1 B and so on. Let C1 , C2 , C3 , ............. be circles with diameters P0 P1 , P1 P2 , P2 P3 , ............... respectively. Suppose the circles C1 , C2 , C3 , ............. are all shaded. The ratio of the area of the unshaded portion of C to that of the original circle C is

CAT/2003(Quantitative Ability)

Question. 38

Let A and B be two solid spheres such that the surface area of B is 300% higher than the surface area of A. The volume of A is found to be k% lower than the volume of B. The value of k must be

CAT/2003(Quantitative Ability)

Question. 39

In the figure below , ABCDEF is a regular hexagon and AOF = 90°. FO is parallel to ED. What is the ratio of the area of the triangle AOF to that of the hexagon ABCDEF?

CAT/2003(Quantitative Ability)

Question. 40

Three horses are grazing within a semi-circular field. In the diagram given below, AB is the diameter of the semi-circular field with centre at O. The horses are tied up at P, R and S such that PO and RO are the radii of semi-circles with centres at P and R respectively, and S is the centre of the circle touching the two semi-circles with diameters AO and OB. The horses tied at P and R can graze within the respective semi–circles and the horse tied at S can graze within the circle centred at S. The percentage of the area of the semi circle with diameter AB that cannot be grazed by the horses is nearest to

CAT/2003(Quantitative Ability)

Question. 41

There are two concentric circles such that the area of the outer circle is four times the area of the inner circle . Let A,B and C be three distinct points on the perimeter of the outer circle such that AB and AC are tangents to the inner circle. If the area of the outer circle is 12 square centimeters then the area (in square centimeters ) of the triangle ABC would be

CAT/2003(Quantitative Ability)

Question. 42

The length of the circumference of a circle equals the perimeter of a triangle of equal sides, and also the perimeter of a square. The areas covered by the circle, triangle , and square are c, t, and s, respectively. Then

CAT/2003(Quantitative Ability)

Question. 43

CAT/2003(Quantitative Ability)

Question. 44

Consider two different cloth-cutting processes. In the first one, n circular cloth pieces are cut from a square cloth piece of side a in the following steps : the original square of side a is divided into n smaller squares, not necessarily of the same size ; then a circle of maximum possible area is cut from each of the smaller squares. In the second process, only one circle of maximum possible area is cut from the square of side a and the process ends there. The cloth pieces remaining after cutting the circles are scrapped in both the processes. The ratio of the total area of scrap cloth generated in the former to that in the latter is

Comprehension

Directions for questions: Read the information given below and answer the questions that follow

Consider a cylinder of height h cms and radius r =π/2 cms as shown in the figure (not drawn to scale). A string of a certain length, when wound on its cylindrical surface, starting at point A and ending at point B, gives a maximum of n turns (in other words, the string’s length is the minimum length required to wind n turns).

CAT/2003(Quantitative Ability)

Question. 45

What is the vertical spacing in cms between two consecutive turns?

Comprehension

Directions for questions: Read the information given below and answer the questions that follow

Consider a cylinder of height h cms and radius r =π/2 cms as shown in the figure (not drawn to scale). A string of a certain length, when wound on its cylindrical surface, starting at point A and ending at point B, gives a maximum of n turns (in other words, the string’s length is the minimum length required to wind n turns).

CAT/2003(Quantitative Ability)

Question. 46

The same string, when wound on the exterior four walls of a cube of side n cms, starting at point C and ending at point D, can give exactly one turn (see figure, not drawn to scale). The length of the string, in cms, is

Comprehension

Directions for questions: Read the information given below and answer the questions that follow

Consider a cylinder of height h cms and radius r =π/2 cms as shown in the figure (not drawn to scale). A string of a certain length, when wound on its cylindrical surface, starting at point A and ending at point B, gives a maximum of n turns (in other words, the string’s length is the minimum length required to wind n turns).

CAT/2003(Quantitative Ability)

Question. 47

In the setup of the previous two questions, how is h related to n?

CAT/2003(Quantitative Ability)

Question. 48

A piece of paper is in the shape of a right angled triangle and is cut along a line that is parallel to the hypotenuse, leaving a smaller triangle. There was 35% reduction in the length of the hypotenuse of the triangle . If the area of the original triangle was 34 square inches before the cut, what is the area (in square inches) of the smaller triangle?

CAT/2003(Quantitative Ability)

Question. 49

A square tin sheet of side 12 inches is converted into a box with open top in the following steps: The sheet is placed horizontally; Then, equal sized squares, each of side x inches, are cut from the four corners of the sheet; Finally, the four resulting sides are bent vertically upwards in the shape of a box. If x is an integer, then what value of x maximizes the volume of the box?

CAT/2003(Quantitative Ability)

Question. 50

Let ABCDEF be a regular hexagon. What is the ratio of the area of the triangle ACE to that of the hexagon ABCDEF?

CAT/2003(Quantitative Ability)

Question. 51

In the figure below (not drawn to scale), rectangle ABCD is inscribed in the circle with center at O. The length of side AB is greater than that of side BC. The ratio of the area of the circle to the area of the rectangle ABCD is π : √3 . The line segment DE intersects AB at E such that ∠ODC = ∠ADE. What is the ratio AE : AD?

CAT/2002(Quantitative Ability)

Question. 52

Four horses are tethered at four corners of a square plot of side 14 metres so that the adjacent horses can just reach one another. There is a small circular pond of area 20 m² at the centre. The area left ungrazed is

CAT/2002(Quantitative Ability)

Question. 53

Neeraj has agreed to mow the front lawn, which is a 20 m by 40 m rectangle. The mower mows a 1 m wide strip. If Neeraj starts at one corner and mows around the lawn toward the centre, about how many times would he go round before he has mowed half the lawn?

CAT/2002(Quantitative Ability)

Question. 54

In the figure given below, ABCD is a rectangle. The area of the isosceles right traingle ABE = 7 cm² ; EC = 3 (BE). The area of ABCD (in cm² ) is

CAT/2002(Quantitative Ability)

Question. 55

The area of the triangle whose vertices are (a, a), (a + 1, a + 1), (a + 2, a) is

Comprehension

Directions for questions: Read the information given below and answer the questions that follow :

Answer these questions based on the following diagram.

In the diagram below :  ∠ABC = ∠DCH = ∠DOE = ∠EHK = ∠FKL = ∠GLM = ∠LMN = 90° and AB = BC = 2CH = 2CD = EH = FK = 2HK = 4KL = 2LM = MN

CAT/2002(Quantitative Ability)

Question. 56

The magnitude of ∠FGO =

Comprehension

Directions for questions: Read the information given below and answer the questions that follow :

Answer these questions based on the following diagram.

In the diagram below :  ∠ABC = ∠DCH = ∠DOE = ∠EHK = ∠FKL = ∠GLM = ∠LMN = 90° and AB = BC = 2CH = 2CD = EH = FK = 2HK = 4KL = 2LM = MN

CAT/2002(Quantitative Ability)

Question. 57

The ratio of the areas of the two quadrangles ABCD and DEFG is

CAT/2001(Quantitative Ability)

Question. 58

A rectangular pool 20 metres wide and 60 metres long is surrounded by a walkway of uniform width. If the total area of the walkway is 516 square metres, how wide, in metres, is the walkway?

CAT/2001(Quantitative Ability)

Question. 59

A square, whose side is 2 metres, has its corners cut a way so as to form an octagon with all sides equal. Then the length of each side of the octagon, in metres is

CAT/2001(Quantitative Ability)

Question. 60

A certain city has a circular wall around it, and this wall has four gates pointing north, south, east and west. A house stands outside the city, three kms north of the north gate, and it can just be seen from a point nine kms east of the south gate. What is the diameter of the wall that surrounds the city?

CAT/2001(Quantitative Ability)

Question. 61

In the diagram, ABCD is a rectangle with AE = EF = FB. What is the ratio of the area of the triangle CEF and that of the rectangle?

CAT/2001(Quantitative Ability)

Question. 62

A ladder leans against a vertical wall. The top of the ladder is 8m above the ground. When the bottom of the ladder is moved 2m farther away from the wall, the top of the ladder rests against the foot of the wall. What is the length of the ladder?

CAT/2001(Quantitative Ability)

Question. 63

Two sides of a plot measure 32 metres and 24 metres and the angle between them is a perfect right angle. The other two sides measure 25 metres each and the other three angles are not right angles.

What is the area of the plot?

CAT/2001(Quantitative Ability)

Question. 64

Euclid has a triangle in mind. Its longest side has length 20 and another of its sides has length 10. Its area is 80. What is the exact length of its third side?

CAT/2000(Quantitative Ability)

Question. 65

There are two tanks, one cylindrical and the other conical. The cylindrical tank contains 500 litres limca more than the conical tank. 200 litres is removed both from the cylindrical and conical tank. Now the cylindrical tank contains double the volume of liquid in the conical tank. What is the capacity of the cylindrical tank in litre?

CAT/2000(Quantitative Ability)

Question. 66

CAT/2000(Quantitative Ability)

Question. 67

What is the area of the region bounded by |x + y| =1 , |x| =1& |y| =1

CAT/1999(Quantitative Ability)

Question. 68

There is a square field of side 500 metres. From one corner of the field a triangular area has to be cordoned off with a straight fence of length 100 metres, using the boundaries of the field as the other two sides. What is the maximum area that can be cordoned of

CAT/1998(Quantitative Ability)

Question. 69

Four identical coins are placed in a square. For each coin the ratio of area to circumference is same as the ratio of circumference to area. Then find the area of the square that is not covered by the coins

CAT/1998(Quantitative Ability)

Question. 70

A cow is tethered at A by a rope. Neither the rope nor the cow is allowed to enter the triangle ABC.

m∠A = 30º

∂(AB) = ∂(AC) = 10 m.

∂(BC) = 6 m

What is the area that can be grazed by the cow if the length of the rope is 8 m?

CAT/1998(Quantitative Ability)

Question. 71

A cow is tethered at A by a rope. Neither the rope nor the cow is allowed to enter the triangle ABC.

m∠A = 30º

∂(AB) = ∂(AC) = 10 m.

∂(BC) = 6 m

What is the area that can be grazed by the cow if the length of the rope is 12 m?

CAT/1998(Quantitative Ability)

Question. 72

Four identical coins are placed in a square. For each coin the ratio of area to circumference is same as the ratio of circumference to area. Then find the area of the square that is not covered by the coins

Comprehension

Directions for questions: Read the information given below and answer the questions that follow :

A cow is tethered at A by a rope. Neither the rope nor the cow is allowed to enter the triangle ABC.

CAT/1998(Quantitative Ability)

Question. 73

What is the area that can be grazed by the cow if the length of the rope is 8 m?

Comprehension

Directions for questions: Read the information given below and answer the questions that follow :

A cow is tethered at A by a rope. Neither the rope nor the cow is allowed to enter the triangle ABC.

CAT/1998(Quantitative Ability)

Question. 74

What is the area that can be grazed by the cow if the length of the rope is 12 m?

CAT/1997(Quantitative Ability)

Question. 75

The adjoining figure shows a set of concentric squares. If the diagonal of the innermost square is 2 units, and if the distance between the corresponding corners of any two successive squares is 1 unit, find the difference between the areas of the eighth and the seventh square, counting from the innermost square

CAT/1997(Quantitative Ability)

Question. 76

In a triangle ABC, points P, Q and R are the mid-points of the sides AB, BC and CA respectively. If the area of the triangle ABC is 20 sq. units, find the area of the triangle PQR

CAT/1997(Quantitative Ability)

Question. 77

In the adjoining figure, points A, B, C and D lie on the circle. AD = 24 and BC = 12. What is the ratio of the area of the triangle CBE to that of the triangle ADE

CAT/1996(Quantitative Ability)

Question. 78

From a circular sheet of paper with a radius 20 cm, four circles of radius 5cm each are cut out. What is the ratio of the uncut to the cut portion?

CAT/1996(Quantitative Ability)

Question. 79

A closed wooden box of thickness 0.5 cm and length 21 cm, width 11 cm, and height 6 cm, is painted inside. The expenses of painting are Rs 70. What is the rate of painting in rupees per sq. cm.?

CAT/1996(Quantitative Ability)

Question. 80

A cube of side 12 cm. is painted red on all the faces and then cut into smaller cubes, each of side 3cm. What is the total number of smaller cubes having none of their faces painted?

CAT/1995(Quantitative Ability)

Question. 81

PQRS is a square. SR is a tangent (at point S) to the circle with centre O and TR=OS. Then, the ratio of area of the circle to the area of the square is

CAT/1995(Quantitative Ability)

Question. 82

In the adjoining figure, AC + AB = 5 AD and AC – AD = 8. Then the area of the rectangle ABCD is

CAT/1995(Quantitative Ability)

Question. 83

The sides of a triangle are 5, 12 and 13 units respectively. A rectangle is constructed which is equal in area to the triangle and has a width of 10 units. Then the perimeter of the rectangle is

CAT/1995(Quantitative Ability)

Question. 84

ABCD is a square of area 4, which is divided into four non overlapping triangles as shown in the fig. Then the sum of the perimeters of the triangles is

CAT/1995(Quantitative Ability)

Question. 85

The figure shows a rectangle ABCD with a semi-circle and a circle inscribed inside it as shown. What is the ratio of the area of the circle to that of the semi-circle?

CAT/1995(Quantitative Ability)

Question. 86

The figure shows a circle of diameter AB and radius 6.5 cm. If chord CA is 5 cm long, find the area of triangle ABC

CAT/1995(Quantitative Ability)

Question. 87

In a rectangle, the difference between the sum of the adjacent sides and the diagonal is half the length of the longer side. What is the ratio of the shorter to the longer side?

CAT/1995(Quantitative Ability)

Question. 88

The sum of the areas of two circles which touch each other externally is 153. If the sum of their radii is 15, find the ratio of the larger to the smaller radius

CAT/1994(Quantitative Ability)

Question. 89

A right circular cone, a right circular cylinder and a hemisphere, all have the same radius, and the heights of cone and cylinder are equal to their diameters. Then their volumes are proportional, respectively, to

CAT/1994(Quantitative Ability)

Question. 90

A right circular cone of height h is cut by a plane parallel to the base and at a distance h/3 from the base, then the volumes of the resulting cone and frustum are in the ratio

CAT/1994(Quantitative Ability)

Question. 91

In ΔACD, AD = AC and ∠C = 2∠E . The distance between parallel lines AB and CD is h.

Then

I. Area of parallelogram ABCD

II. Area of ΔADE