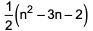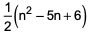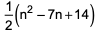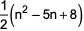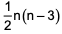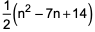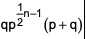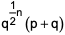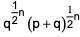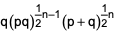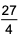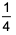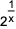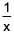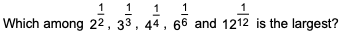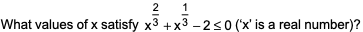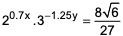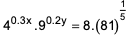CAT Quantitative Ability Questions | CAT Number System questions
CAT Number System | CAT QA Questions | Types of Numbers; Surds and Indices; Arithmetic Calculations; Division and Divisibility Test; Simplification and Rationalization ; HCF and LCM; Fractions; Comparison of Fractions; Numeration Systems; Conversion between Numeration Systems.CAT/2024.3(Quantitative Ability)
Question. 2
The number of all positive integers up to 500 with non-repeating digits is
378
CAT/2024.2(Quantitative Ability)
Question. 6
P, Q, R and S are four towns. One can travel between P and Q along 3 direct paths, between Q and S along 4 direct paths, and between P and R along 4 direct paths. There is no direct path between P and S, while there are few direct paths between Q and R, and between R and S. One can travel from P to S either via Q, or via R, or via Q followed by R, respectively, in exactly 62 possible ways. One can also travel from Q to R either directly, or via P, or via S, in exactly 27 possible ways. Then, the number of direct paths between Q and R is
CAT/2024.1(Quantitative Ability)
Question. 7
The sum of all four-digit numbers that can be formed with the distinct non-zero digits a,b,c">a,b,ca,b,c, and d">dd, with each digit appearing exactly once in every number, is 153310+n">153310+n153310+n, where n">nn is a single digit natural number. Then, the value of (a+b+c+d+n)">(a+b+c+d+n)(a+b+c+d+n) is
31
CAT/2023.1(Quantitative Ability)
Question. 11
The number of all natural numbers up to 1000 with non-re04peating digits is
19
CAT/2021.1(Quantitative Ability)
Question. 13
How many three-digit numbers are greater than 100 and increase by 198 when the three digits are arranged in the reverse order?
70
CAT/2021.2(Quantitative Ability)
Question. 14
For a 4-digit number, the sum of its digits in the thousands, hundreds and tens places is 14, the sum of its digits in the hundreds, tens, and units places is 15, and the tens place digit is 4 more than the units place digit. Then the highest possible 4-digit number satisfying the above conditions is
4195
CAT/2021.3(Quantitative Ability)
Question. 15
A four-digit number is formed by using only the digits 1, 2 and 3 such that both 2 and 3 appear at least once. The number of all such four-digit numbers is
50
CAT/2021.3(Quantitative Ability)
Question. 17
The number of distinct pairs of integers (m,n) satisfying |1 + mn| < |m + n| < 5 is
12
CAT/2020.1(Quantitative Ability)
Question. 18
How many 3-digit numbers are there, for which the product of their digits is more than 2 but less than 7?
21
36
CAT/2020.1(Quantitative Ability)
Question. 24
A gentleman decided to treat a few children in the following manner. He gives half of his total stock of toffees and one extra to the first child, and then the half of the remaining stock along with one extra to the second and continues giving away in this fashion. His total stock exhausts after he takes care of 5 children. How many toffees were there in his stock initially?
62
CAT/2020.2(Quantitative Ability)
Question. 27
If x and y are positive real numbers satisfying x + y = 102, then the minimum possible value of 2601(1 + 1x">1/x)(1 + 1y">1/y) is
2704
CAT/2020.2(Quantitative Ability)
Question. 28
How many 4-digit numbers, each greater than 1000 and each having all four digits distinct, are there with 7 coming before 3?
315
24
CAT/2019.1(Quantitative Ability)
Question. 38
If a1 + a2 + a3 + ... + an = 3(2n+1 - 2), then a11 equals [TITA]
6144
CAT/2019.2(Quantitative Ability)
Question. 45
How many factors of 24 x 35 x 104 are perfect squares which are greater than 1?
44
CAT/2019.2(Quantitative Ability)
Question. 47
In a six-digit number, the sixth, that is, the rightmost, digit is the sum of the first three digits, the fifth digit is the sum of first two digits, the third digit is equal to the first digit, the second digit is twice the first digit and the fourth digit is the sum of fifth and sixth digits. Then, the largest possible value of the fourth digit is
CAT/2019.2(Quantitative Ability)
Question. 49
If (2n+1) + (2n+3) + (2n+5) + ... + (2n+47) = 5280 , then what is the value of 1+2+3+ ... +n ?
4851
CAT/2018.1(Quantitative Ability)
Question. 50
While multiplying three real numbers, Ashok took one of the numbers as 73 instead of 37. As a result, the product went up by 720. Then the minimum possible value of the sum of squares of the other two numbers is
40
CAT/2018.1(Quantitative Ability)
Question. 51
How many numbers with two or more digits can be formed with the digits 1, 2, 3, 4, 5, 6, 7, 8, and 9 so that in every such number, each digit is used at most once and the digits appear in the ascending order?
502
CAT/2018.2(Quantitative Ability)
Question. 55
Let t1, t2,… be real numbers such that t1+ t2 +... + tn = 2n2 + 9n + 13, for every positive integer n ≥ 2. If tk=103, then k equals
24
CAT/2018.2(Quantitative Ability)
Question. 56
If N and x are positive integers such that NN = 2160 and N2 + 2N is an integral multiple of 2x, then the largest possible x is
10
CAT/2018.2(Quantitative Ability)
Question. 63
The arithmetic mean of x, y and z is 80, and that of x, y, z, u and v is 75, where u = (x+y)/2 ) and v= (y+z)/2. If x ≥ z, then the minimum possible value of x is
105
CAT/2017.2(Quantitative Ability)
Question. 67
The numbers 1, 2,..., 9 are arranged in a 3 X 3 square grid in such a way that each number occurs once and the entries along each column, each row, and each of the two diagonals add up to the same value. If the top left and the top right entries of the grid are 6 and 2, respectively, then the bottom middle entry is
CAT/2017.2(Quantitative Ability)
Question. 69
Let a1, a2, a3, a4, a5 be a sequence of five consecutive odd numbers. Consider a new sequence of five consecutive even numbers ending with 2a3. If the sum of the numbers in the new sequence is 450, then a5 is
51
CAT/2008(Quantitative Ability)
Question. 73
The integers 1, 2, ..., 40 are written on a blackboard. The following operation is then repeated 39 times: In each repetition, any two numbers, say a and b, currently on the blackboard are erased and a new number a + b – 1 is written. What will be the number left on the board at the end?
The integers 1, 2, ..., 40 are written on a blackboard. The following operation is then repeated 39 times: In each repetition, any two numbers, say a and b, currently on the blackboard are erased and a new number a + b – 1 is written. What will be the number left on the board at the end?
CAT/2008(Quantitative Ability)
Question. 76
A shop stores x kg of rice. The first customer buys half this amount plus half a kg of rice. The second customer buys half the remaining amount plus half a kg of rice. Then the third customer also buys half the remaining amount plus half a kg of rice. Thereafter, no rice is left in the shop. Which of the following best describes the value of x?
Comprehension
Directions for Questions:
Mark (1) if Q can be answered from A alone but not from B alone.
Mark (2) if Q can be answered from B alone but not from A alone.
Mark (3) if Q can be answered from A alone as well as from B alone.
Mark (4) if Q can be answered from A and B together but not from any of them alone.
Mark (5) if Q cannot be answered even from A and B together.
In a single elimination tournament, any player is eliminated with a single loss. The tournament is played in multiple rounds subject to the following rules :
(a) If the number of players, say n, in any round is even, then the players are grouped into n/2 pairs. The players in each pair play a match against each other and the winner moves on to the next round.
(b) If the number of players, say n, in any round is odd, then one of them is given a bye, that is he automatically moves on to the next round. The remaining (n–1) players are grouped into (n–1)/2 pairs. The players in each pair play a match against each other and the winner moves on to the next round. No player gets more than one bye in the entire tournament.
Thus, if n is even, then n/2 players move on to the next round while if n is odd, then (n+1)/2 players move on to the next round. The process is continued till the final round, which obviously is played between two players. The winner in the final round is the champion of the tournament.
CAT/2008(Quantitative Ability)
Question. 80
What is the number of Matches played by the champion?
A. The entry list for the tournament consists of 83 players.
B. The champion received one bye.
Comprehension
Directions for Questions:
Mark (1) if Q can be answered from A alone but not from B alone.
Mark (2) if Q can be answered from B alone but not from A alone.
Mark (3) if Q can be answered from A alone as well as from B alone.
Mark (4) if Q can be answered from A and B together but not from any of them alone.
Mark (5) if Q cannot be answered even from A and B together.
In a single elimination tournament, any player is eliminated with a single loss. The tournament is played in multiple rounds subject to the following rules :
(a) If the number of players, say n, in any round is even, then the players are grouped into n/2 pairs. The players in each pair play a match against each other and the winner moves on to the next round.
(b) If the number of players, say n, in any round is odd, then one of them is given a bye, that is he automatically moves on to the next round. The remaining (n–1) players are grouped into (n–1)/2 pairs. The players in each pair play a match against each other and the winner moves on to the next round. No player gets more than one bye in the entire tournament.
Thus, if n is even, then n/2 players move on to the next round while if n is odd, then (n+1)/2 players move on to the next round. The process is continued till the final round, which obviously is played between two players. The winner in the final round is the champion of the tournament.
CAT/2008(Quantitative Ability)
Question. 81
If the number of players, say n, in the first round was between 65 and 128, then what is the exact value of n?
A. Exactly one player received a bye in the entire tournament.
B. One player received a bye while moving on to the fourth round from the third round.
CAT/2008(Quantitative Ability)
Question. 83
Three consecutive positive integers are raised to the first, second and third powers respectively and then added. The sum so obtained is perfect square whose square root equals the total of the three original integers. Which of the following best describes the minimum, say m, of these three integers?
CAT/2007(Quantitative Ability)
Question. 85
A confused bank teller transposed the rupees and paise when he cashed a cheque for Shailaja. giving her rupees instead of paise and paise instead of rupees. After buying a toffee for 50 paise, Shailaja noticed that she was left with exactly three times as much as the amount on the cheque.
Which of the following is a valid statement about the cheque amount?
(1) Over Rupees 13 but less than Rupees 14
(2) Over Rupees 7 but less than Rupees 8
(3) Over Rupees 22 but less than Rupees 23
(4) Over Rupees 18 but less than Rupees 19
(5) Over Rupees 4 but less than Rupees 5
Comprehension
Directions for Questions 7 to 10: Each question is followed by two statements A and B. Indicate your response based on the following directives.
Mark (1) if the questions can be answered using A alone but not using B alone.
Mark (2) if the question can be answered using B alone but not using A alone.
Mark (3) if the question can be answered using A and B together, but not using either A or B alone.
Mark (4) if the question cannot be answered even using A and B together.
CAT/2007(Quantitative Ability)
Question. 87
Consider integers x, y, z. What is the minimum possible value of x2y2z2 + + ?
A: x + y + z = 89.
B: Among x, y, z two are equal.
Comprehension
Directions for Questions 15 and 16:
Answer the following questions based on the information given below:
Let S be the set of all pairs (i, j) where 1≤ i < j ≤ n and n ≥ 4 . Any two distinct members of S are called “friends” if they have one constituent of the pairs in common and “enemies” otherwise. For example, if n = 4, then S = {(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)}. Here, (1, 2) and (1, 3) are friends, (1, 2) and (2, 3) are also friends, but (1, 4) and (2, 3) are enemies.
Comprehension
Directions for Questions 15 and 16:
Answer the following questions based on the information given below:
Let S be the set of all pairs (i, j) where 1≤ i < j ≤ n and n ≥ 4 . Any two distinct members of S are called “friends” if they have one constituent of the pairs in common and “enemies” otherwise. For example, if n = 4, then S = {(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)}. Here, (1, 2) and (1, 3) are friends, (1, 2) and (2, 3) are also friends, but (1, 4) and (2, 3) are enemies.
CAT/2007(Quantitative Ability)
Question. 90
In a tournament, there are n teams T1 , T2 ,..., Tn , with n > 5. Each team consists of ‘k’ players, k > 3. The following pairs of teams have one player in common:
T1& T2 ,T2 & T3 , ......, Tn, and Tn & T1
No other pair of teams has any player in common. How many players are participating in the tournament, considering all the ‘n’ teams together?
CAT/2004(Quantitative Ability)
Question. 111
Let n( > 1) be a composite integer such that √n is not an integer. Consider the following statements
I : n has a perfect integer-valued divisor which is greater than 1 and less than √n .
II : n has a perfect integer-valued divisor which is greater than √n but less than n
Then,
CAT/2003(Quantitative Ability)
Question. 119
The seven basic symbols in a certain numeral system and their respective values are as follow :
I = 1 , V = 5 , X = 10, L = 50, C = 100, D = 500, and M = 1000
In general, the symbols in the numeral system are read from left to right, starting with the symbol representing the largest value; the same symbol cannot occur continuously more than three times; the value of the numeral is the sum of the values of the symbols. For example , XXVII = 10 + 10 + 5 + 1 + 1= 27. An exception to the left to right reading occurs when a symbol is followed immediately by a symbol of greater value; then, the smaller value is subtracted from the larger. For example, XLVI = (50 – 10) + 5 + 1 = 46.
The value of the numeral MDCCLXXXVII is
CAT/2003(Quantitative Ability)
Question. 120
The seven basic symbols in a certain numeral system and their respective values are as follow :
I = 1 , V = 5 , X = 10, L = 50, C = 100, D = 500, and M = 1000
In general, the symbols in the numeral system are read from left to right, starting with the symbol representing the largest value; the same symbol cannot occur continuously more than three times; the value of the numeral is the sum of the values of the symbols. For example , XXVII = 10 + 10 + 5 + 1 + 1= 27. An exception to the left to right reading occurs when a symbol is followed immediately by a symbol of greater value; then, the smaller value is subtracted from the larger.
For example, XLVI = (50 – 10) + 5 + 1 = 46.
The value of the numeral MCMXCIX is
CAT/2003(Quantitative Ability)
Question. 121
The seven basic symbols in a certain numeral system and their respective values are as follow :
I = 1 , V = 5 , X = 10, L = 50, C = 100, D = 500, and M = 1000
In general, the symbols in the numeral system are read from left to right, starting with the symbol representing the largest value; the same symbol cannot occur continuously more than three times; the value of the numeral is the sum of the values of the symbols. For example , XXVII = 10 + 10 + 5 + 1 + 1= 27. An exception to the left to right reading occurs when a symbol is followed immediately by a symbol of greater value; then, the smaller value is subtracted from the larger.
For example, XLVI = (50 – 10) + 5 + 1 = 46.
Which of the following can represent the numeral for 1995?
I. MCMLXXV
II. MCMXCV
III. MVD
IV. MVM
CAT/2002(Quantitative Ability)
Question. 124
At a book store, “MODERN BOOK STORE” is flashed using neon lights. The words are individually flashed at intervals of 2(1/2), 4(1/4), 5(1/8) seconds respectively, and each word is put off after a second. The least time after which the full name of the bookstore can be read again is
CAT/2001(Quantitative Ability)
Question. 129
In a 4 - digit number, the sum of the first two digits is equal to that of the last two digits. The sum of the first and last digits is equal to the third digit. Finally, the sum of the second and fourth digits is twice the sum of the other two digits. What is the third digit of the number?
CAT/2001(Quantitative Ability)
Question. 132
Every ten years the Indian government counts all the people living in the country. Suppose that the director of the census has reported the following data on two neighbouring villages Chota Hazri and Mota Hazri
Chota Hazri has 4,522 fewer males than Mota hazri.
Mota Hazri has 4,020 more females than males.
Chota Hazri has twice as many females as males.
Chota Hazri has 2,910 fewer females than Mota Hazri.
What is the total number of males in Chota Hazri?
CAT/1998(Quantitative Ability)
Question. 153
Number of students who have opted the subjects A, B, C are 60, 84, 108 respectively. The examination is to be conducted for these students such that only the students of the same subject are allowed in one room. Also the number of students in each room must be same. What is the minimum number of rooms that should be arranged to meet all these conditions?
CAT/1996(Quantitative Ability)
Question. 166
A salesman enters the quantity sold and the price into the computer. Both the numbers are two-digit numbers. Once, by mistake, both the numbers were entered with their digits interchanged. The total sales value remained the same, i.e. Rs 1148, but the inventory reduced by 54.
What is the actual price per piece ?
CAT/1996(Quantitative Ability)
Question. 167
A salesman enters the quantity sold and the price into the computer. Both the numbers are two-digit numbers. Once, by mistake, both the numbers were entered with their digits interchanged. The total sales value remained the same, i.e. Rs 1148, but the inventory reduced by 54.
What is the actual quantity sold ?

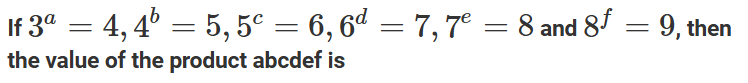

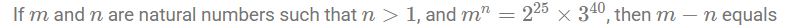

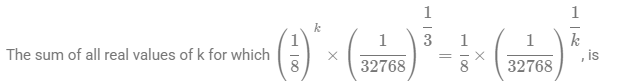
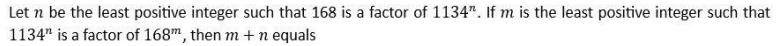

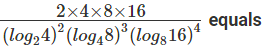
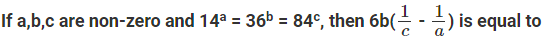

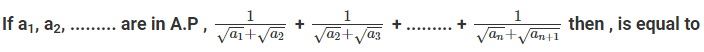
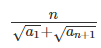
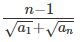
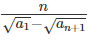
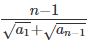
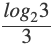
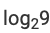
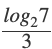
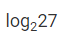
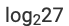
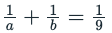
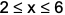
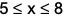
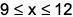
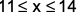
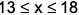
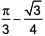
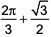
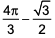
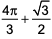
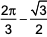
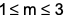

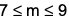
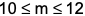
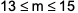
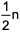
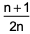
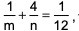 where ‘n’ is an odd integer less than 60?
where ‘n’ is an odd integer less than 60?