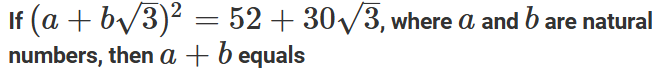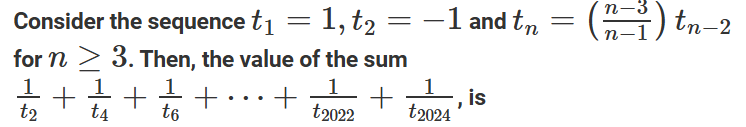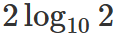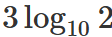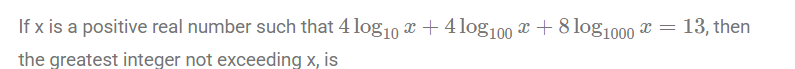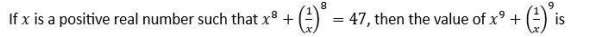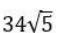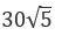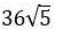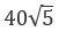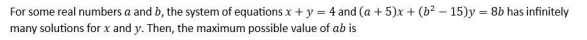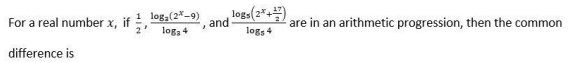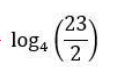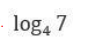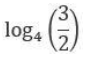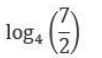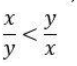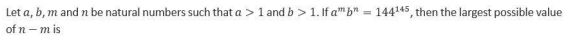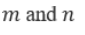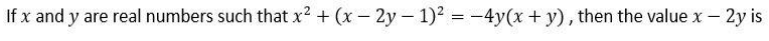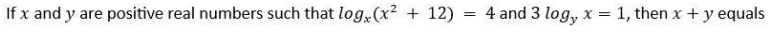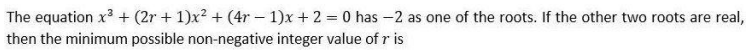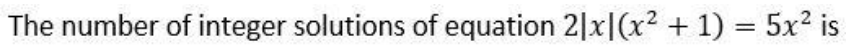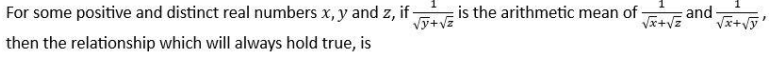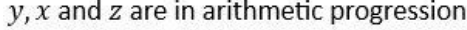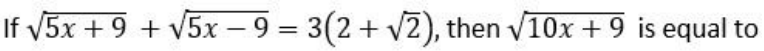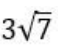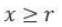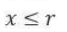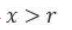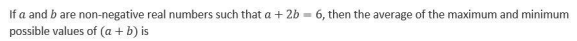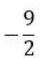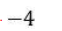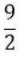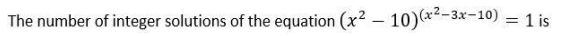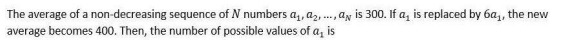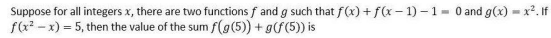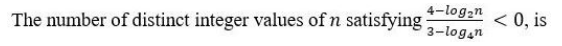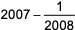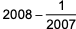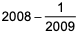CAT Quantitative Ability Questions | CAT Algebra questions

Comprehension

N/A

CAT/2024.3(Quantitative Ability)

Question. 1

The number of distinct integer solutions (x,y)">(x,y) of the equation |x+y|+|x−y|=2">|x+y|+|x−y|=2, is

Comprehension

N/A

CAT/2024.3(Quantitative Ability)

Question. 2

Comprehension

N/A

CAT/2024.3(Quantitative Ability)

Question. 3

Comprehension

N/A

CAT/2024.3(Quantitative Ability)

Question. 4

Comprehension

N/A

CAT/2024.3(Quantitative Ability)

Question. 5

The number of distinct real values of x">x, satisfying the equation max{x,2}−min{x,2}=|x+2|−|x−2|">max{x,2} − min{x,2}=|x+2|−|x−2|, is

Comprehension

N/A

CAT/2024.3(Quantitative Ability)

Question. 6

Comprehension

N/A

CAT/2024.2(Quantitative Ability)

Question. 7

Comprehension

N/A

CAT/2024.2(Quantitative Ability)

Question. 8

Comprehension

N/A

CAT/2024.2(Quantitative Ability)

Question. 9

Comprehension

N/A

CAT/2024.2(Quantitative Ability)

Question. 10

Comprehension

N/A

CAT/2024.2(Quantitative Ability)

Question. 11

Comprehension

N/A

CAT/2024.2(Quantitative Ability)

Question. 12

Comprehension

N/A

CAT/2024.2(Quantitative Ability)

Question. 13

Comprehension

N/A

CAT/2024.2(Quantitative Ability)

Question. 14

Comprehension

N/A

CAT/2024.2(Quantitative Ability)

Question. 15

A company has 40 employees whose names are listed in a certain order. In the year 2022, the average bonus of the first 30 employees was Rs. 40000, of the last 30 employees was Rs. 60000, and of the first 10 and last 10 employees together was Rs. 50000. Next year, the average bonus of the first 10 employees increased by 100%, of the last 10 employees increased by 200% and of the remaining employees was unchanged. Then, the average bonus, in rupees, of all the 40 employees together in the year 2023 was

Comprehension

N/A

CAT/2024.2(Quantitative Ability)

Question. 16

A vessel contained a certain amount of a solution of acid and water. When 2 litres of water was added to it, the new solution had 50% acid concentration. When 15 litres of acid was further added to this new solution, the final solution had 80% acid concentration. The ratio of water and acid in the original solution was

Comprehension

N/A

CAT/2024.2(Quantitative Ability)

Question. 17

When Rajesh's age was same as the present age of Garima, the ratio of their ages was 3 : 2. When Garima's age becomes the same as the present age of Rajesh, the ratio of the ages of Rajesh and Garima will become

Comprehension

N/A

CAT/2024.1(Quantitative Ability)

Question. 18

Comprehension

N/A

CAT/2024.1(Quantitative Ability)

Question. 19

Comprehension

N/A

CAT/2024.1(Quantitative Ability)

Question. 20

Comprehension

N/A

CAT/2024.1(Quantitative Ability)

Question. 21

Comprehension

N/A

CAT/2024.1(Quantitative Ability)

Question. 22

Comprehension

N/A

CAT/2024.1(Quantitative Ability)

Question. 23

Comprehension

N/A

CAT/2024.1(Quantitative Ability)

Question. 24

CAT/2023.3(Quantitative Ability)

Question. 25

CAT/2023.3(Quantitative Ability)

Question. 26

CAT/2023.3(Quantitative Ability)

Question. 27

CAT/2023.3(Quantitative Ability)

Question. 28

CAT/2023.3(Quantitative Ability)

Question. 29

CAT/2023.3(Quantitative Ability)

Question. 30

CAT/2023.3(Quantitative Ability)

Question. 31

CAT/2023.3(Quantitative Ability)

Question. 32

The number of coins collected per week by two coin-collectors A and B are in the ratio 3 : 4. If the total number of coins collected by A in 5 weeks is a multiple of 7, and the total number of coins collected by B in 3 weeks is a multiple of 24, then the minimum possible number of coins collected by A in one week is

CAT/2023.3(Quantitative Ability)

Question. 33

CAT/2023.3(Quantitative Ability)

Question. 34

CAT/2023.3(Quantitative Ability)

Question. 35

CAT/2023.2(Quantitative Ability)

Question. 36

CAT/2023.2(Quantitative Ability)

Question. 37

CAT/2023.2(Quantitative Ability)

Question. 38

CAT/2023.2(Quantitative Ability)

Question. 39

CAT/2023.2(Quantitative Ability)

Question. 40

CAT/2023.2(Quantitative Ability)

Question. 41

CAT/2023.2(Quantitative Ability)

Question. 42

CAT/2023.2(Quantitative Ability)

Question. 43

CAT/2023.2(Quantitative Ability)

Question. 44

CAT/2023.2(Quantitative Ability)

Question. 45

CAT/2023.1(Quantitative Ability)

Question. 46

CAT/2023.1(Quantitative Ability)

Question. 47

CAT/2023.1(Quantitative Ability)

Question. 48

CAT/2023.1(Quantitative Ability)

Question. 49

CAT/2023.1(Quantitative Ability)

Question. 50

CAT/2023.1(Quantitative Ability)

Question. 51

CAT/2023.1(Quantitative Ability)

Question. 52

CAT/2023.1(Quantitative Ability)

Question. 53

CAT/2022.3(Quantitative Ability)

Question. 54

CAT/2022.3(Quantitative Ability)

Question. 55

CAT/2022.3(Quantitative Ability)

Question. 56

CAT/2022.3(Quantitative Ability)

Question. 57

The arithmetic mean of all the distinct numbers that can be obtained by rearranging the digits in 1421, including itself, is

CAT/2022.3(Quantitative Ability)

Question. 58

A donation box can receive only cheques of ₹100, ₹250, and ₹500. On one good day, the donation box was found to contain exactly 100 cheques amounting to a total sum of ₹15250. Then, the maximum possible number of cheques of ₹500 that the donation box may have contained, is

CAT/2022.3(Quantitative Ability)

Question. 59

The average of all 3-digit terms in the arithmetic progression 38, 55, 72, ..., is

CAT/2022.3(Quantitative Ability)

Question. 60

CAT/2022.3(Quantitative Ability)

Question. 61

CAT/2022.2(Quantitative Ability)

Question. 62

CAT/2022.2(Quantitative Ability)

Question. 63

CAT/2022.2(Quantitative Ability)

Question. 64

CAT/2022.2(Quantitative Ability)

Question. 65

CAT/2022.2(Quantitative Ability)

Question. 66

CAT/2022.2(Quantitative Ability)

Question. 67

CAT/2022.2(Quantitative Ability)

Question. 68

CAT/2022.2(Quantitative Ability)

Question. 69

CAT/2022.2(Quantitative Ability)

Question. 70

CAT/2022.2(Quantitative Ability)

Question. 71

CAT/2022.2(Quantitative Ability)

Question. 72

CAT/2022.1(Quantitative Ability)

Question. 73

CAT/2022.1(Quantitative Ability)

Question. 74

CAT/2022.1(Quantitative Ability)

Question. 75

CAT/2022.1(Quantitative Ability)

Question. 76

CAT/2022.1(Quantitative Ability)

Question. 77

CAT/2022.1(Quantitative Ability)

Question. 78

CAT/2022.1(Quantitative Ability)

Question. 79

CAT/2022.1(Quantitative Ability)

Question. 80

CAT/2022.1(Quantitative Ability)

Question. 81

In a class of 100 students, 73 like coffee, 80 like tea and 52 like lemonade. It may be possible that some students do not like any of these three drinks. Then the difference between the maximum and minimum possible number of students who like all the three drinks is

CAT/2021.1(Quantitative Ability)

Question. 82

CAT/2021.1(Quantitative Ability)

Question. 83

f(x) = (x² + 2x - 15)/(x²-7x-18) is negative if and only if

CAT/2021.1(Quantitative Ability)

Question. 84

If "r" is a constant such that | x² - 4x - 13 | = r has exactly three distinct real roots, then the value of "r" is

CAT/2021.2(Quantitative Ability)

Question. 85

Three positive integers x, y and z are in arithmetic progression. If y − x > 2 and xyz = 5(x + y + z), then z − x equals

CAT/2021.2(Quantitative Ability)

Question. 86

For a sequence of real numbers x₁, x₂, ...... , x_n, if x₁ - x₂ + x₃ - ..... + (-1)ⁿ⁺¹ x_n = n² + 2n for all natural numbers n, then the sum x₄₉ + x₅₀ equals

CAT/2021.2(Quantitative Ability)

Question. 87

If log₂[3 + log₃{4 + log₄(x-1)}] - 2 = 0, then 4x equals

CAT/2021.2(Quantitative Ability)

Question. 88

Suppose one of the roots of the equation a x² - b x + c = 0 is 2 + √3, where a, b and c are rational numbers and a ≠ 0. If b = c³ then |a| equals

CAT/2021.2(Quantitative Ability)

Question. 89

For all possible integers "n" satisfying 2.25 ≤ 2 + 2ⁿ⁺² ≤ 202, the number of integer values of 3+ 3ⁿ⁺¹ is

CAT/2021.3(Quantitative Ability)

Question. 90

If 3x + 2|y| + y = 7 and x + |x| + 3y = 1, then x + 2y is

CAT/2021.3(Quantitative Ability)

Question. 91

The arithmetic mean of scores of 25 students in an examination is 50. Five of these students top the examination with the same score. If the scores of the other students are distinct integers with the lowest being 30, then the maximum possible score of the toppers is

CAT/2021.3(Quantitative Ability)

Question. 92

CAT/2020.1(Quantitative Ability)

Question. 93

The number of real-valued solutions of the equation 2^x + 2^-x = 2 - (x - 2)² is

CAT/2020.1(Quantitative Ability)

Question. 94

If x = (4096)^7+4√3, then which of the following equals 64?

CAT/2020.1(Quantitative Ability)

Question. 95

 

The number of distinct real roots of the equation

CAT/2020.1(Quantitative Ability)

Question. 96

How many distinct positive integer-valued solutions exist to the equation (x² - 7x + 11)^{(x2 - 13x + 42)} = 1?

CAT/2020.2(Quantitative Ability)

Question. 97

The number of pairs of integers(x,y) satisfying x ≥ y ≥ -20 and 2x + 5y = 99 is

CAT/2020.2(Quantitative Ability)

Question. 98

CAT/2020.2(Quantitative Ability)

Question. 99

If x and y are non-negative integers such that x + 9 = z, y + 1 = z and x + y < z + 5, then the maximum possible value of 2x + y equals

CAT/2020.2(Quantitative Ability)

Question. 100

The number of integers that satisfy the equality (x² - 5x + 7)^{x + 1} = 1 is

CAT/2020.2(Quantitative Ability)

Question. 101

In how many ways can a pair of integers (x , a) be chosen such that x² − 2 | x | + | a - 2 | = 0 ?

CAT/2020.2(Quantitative Ability)

Question. 102

Aron bought some pencils and sharpeners. Spending the same amount of money as Aron, Aditya bought twice as many pencils and 10 less sharpeners. If the cost of one sharpener is 2 more than the cost of a pencil, then the minimum possible number of pencils bought by Aron and Aditya together is

CAT/2020.3(Quantitative Ability)

Question. 103

If x₁ = -1 and x_m = x_{m + 1} + (m + 1) for every positive integer m, then x₁₀₀ equals

CAT/2020.3(Quantitative Ability)

Question. 104

Let k be a constant. The equations kx + y = 3 and 4x + ky = 4 have a unique solution if and only if

CAT/2020.3(Quantitative Ability)

Question. 105

Let m and n be positive integers, If x² + mx + 2n = 0 and x² + 2nx + m = 0 have real roots, then the smallest possible value of m + n is

CAT/2019.1(Quantitative Ability)

Question. 106

If (5.55)^x = (0.555)^y = 1000, then the value of (1x">1/x)- (1y">1/y) is

CAT/2019.1(Quantitative Ability)

Question. 107

The number of the real roots of the equation 2cos(x(x + 1)) = 2^x + 2^-x is

CAT/2019.1(Quantitative Ability)

Question. 108

The number of solutions of the equation |x|(6x² + 1) = 5x² is

CAT/2019.1(Quantitative Ability)

Question. 109

The product of the distinct roots of |x² - x - 6| = x + 2 is

CAT/2019.2(Quantitative Ability)

Question. 110

CAT/2019.2(Quantitative Ability)

Question. 111

Let A be a real number. Then the roots of the equation x² - 4x - log₂A = 0 are real and distinct if and only if

CAT/2019.2(Quantitative Ability)

Question. 112

CAT/2019.2(Quantitative Ability)

Question. 113

The quadratic equation x² + bx + c = 0 has two roots 4a and 3a, where a is an integer. Which of the following is a possible value of b² + c?

CAT/2019.2(Quantitative Ability)

Question. 114

If 5^x - 3^y = 13438 and 5^x-1 + 3^y+1 = 9686 , then x+y equals

CAT/2018.1(Quantitative Ability)

Question. 115

If x is a positive quantity such that 2^x = 3^log₅2 , then x is equal to

CAT/2018.1(Quantitative Ability)

Question. 116

CAT/2018.1(Quantitative Ability)

Question. 117

If u² + (u−2v−1)² = −4v(u + v), then what is the value of u + 3v?

CAT/2018.1(Quantitative Ability)

Question. 118

Given that x²⁰¹⁸ y²⁰¹⁷ = 1/2 and x²⁰¹⁶ y²⁰¹⁹ = 8, the value of x² + y³ is

CAT/2018.1(Quantitative Ability)

Question. 119

If log₂(5 + log₃a) = 3 and log₅(4a + 12 + log₂b) = 3, then a + b is equal to

CAT/2018.2(Quantitative Ability)

Question. 120

If a and b are integers such that 2x² − ax + 2 ＞ 0 and x² − bx + 8 ≥ 0 for all real numbers x, then the largest possible value of 2a − 6b is

CAT/2017.1(Quantitative Ability)

Question. 121

If a and b are integers of opposite signs such that (a + 3)² : b² = 9 : 1 and (a - 1)² : (b - 1)² = 4 : 1, then the ratio a² : b² is

CAT/2017.1(Quantitative Ability)

Question. 122

If x + 1 = x² and x > 0, then 2x⁴ is:

CAT/2017.1(Quantitative Ability)

Question. 123

The value of log_0.008√5 + log_√381 – 7 is equal to

CAT/2017.1(Quantitative Ability)

Question. 124

If 9^{2x – 1} – 81^x-1 = 1944, then x is

CAT/2017.1(Quantitative Ability)

Question. 125

For how many integers n, will the inequality (n – 5) (n – 10) – 3(n – 2) ≤ 0 be satisfied? 

 

 

CAT/2017.1(Quantitative Ability)

Question. 126

If a, b, c, and d are integers such that a + b + c + d = 30, then the minimum possible value of (a - b)² + (a - c)² + (a - d)² is

CAT/2017.2(Quantitative Ability)

Question. 127

If x is a real number such that log₃5 = log₅(2 + x), then which of the following is true?

CAT/2017.2(Quantitative Ability)

Question. 128

If log(2^a × 3^b × 5^c) is the arithmetic mean of log(2² × 3³ × 5), log(2⁶ × 3 × 5⁷), and log(2 × 3² × 5⁴), then a equals

CAT/2008(Quantitative Ability)

Question. 129

Find the sum of:-

 

CAT/2007(Quantitative Ability)

Question. 130

A quadratic function ƒ(x) attains a maximum of 3 at x = 1. The value of the function at x = 0 is 1. What is the value ƒ(x) at x = 10?

CAT/2006(Quantitative Ability)

Question. 131

The graph of y - x against y + x is as shown below. (All graphs in this question are drawn to scale and the same scale has been used on each axis.)

Which of the following shows the graph of y against x?

CAT/2006(Quantitative Ability)

Question. 132

Let f(x) = max(2x + 1, 3 - 4x), where x is any real number. Then the minimum possible value of f(x) is:

CAT/2006(Quantitative Ability)

Question. 133

If logy x = (a . logz y) = (b . logx z) = ab, then which of the following pairs of values for (a, b) is not possible?

CAT/2006(Quantitative Ability)

Question. 134

The number of solutions of the equation 2x + y = 40 where both x and y are positive integers and x ≤ y is:

CAT/2005(Quantitative Ability)

Question. 135

CAT/2005(Quantitative Ability)

Question. 136

A telecom service provider engages male and female operators for answering 1000 calls per day. A male operator can handle 40 calls per day whereas a female operator can handle 50 calls per day. The male and the female operators get a fixed wages of Rs. 250 and Rs. 300 per day respectively. In addition, a male operator gets Rs. 15 per call he answers and a female operator gets Rs. 10 per call she answer. To minimize the total cost, how many male operators should the service provider employ assuming he has to employ more than 7 of the 12 female operators available for the job?

CAT/2005(Quantitative Ability)

Question. 137

CAT/2004(Quantitative Ability)

Question. 138

The total number of integer pairs (x, y) satisfying the equation x + y = xy is

CAT/2004(Quantitative Ability)

Question. 139

CAT/2004(Quantitative Ability)

Question. 140

For which value of k does the following pair of equations yield a unique solution for x such that the solution is positive?

x² – y² = 0

(x – k)² + y² = 1

CAT/2004(Quantitative Ability)

Question. 141

If the sum of the first 11 terms of an arithmetic progression equals that of the first 19 terms, then what is the sum of the first 30 terms?

CAT/2004(Quantitative Ability)

Question. 142

If log₁₀ x – log₁₀ √x = 2log_x 10, then a possible value of x is given by

CAT/2004(Quantitative Ability)

Question. 143

Consider the sequence of numbers a₁, a₂, a₃, ........... to infinity where a₁ = 81.33 and a₂ = – 19 and a_j = a_j–1–a_j–2 for j ≥3. What is the sum of the first 6002 terms of this sequence?

CAT/2004(Quantitative Ability)

Question. 144

CAT/2004(Quantitative Ability)

Question. 145

If a₁ = 1 and a_n+1 – 3a_n+2 = 4n for every positive integer n, then a₁₀₀ equals

CAT/2003(Quantitative Ability)

Question. 146

Which one of the following conditions must p, q and r satisfy so that the following system of linear simultaneous equations has at least one solution, such that p + q + r ≠ 0 ?

x + 2y 3z = p ; 2x + 6y 11z = q ; x 2y + 7z = r

CAT/2003(Quantitative Ability)

Question. 147

The number of non-negative real roots of 2^x - x  - 1 = 0 equals

CAT/2003(Quantitative Ability)

Question. 148

Let a, b, c, d be four integers such that a + b + c + d = 4m + 1 where m is a positive integer. Given m, which one of the following is necessarily true?

CAT/2003(Quantitative Ability)

Question. 149

Let p and q be the roots of the quadratic equation x² - (α - 2)x - α - 1 = 0. What is the minimum possible value of p² + q² ?

CAT/2003(Quantitative Ability)

Question. 150

If the product of n positive real numbers is unity, then their sum is necessarily

CAT/2003(Quantitative Ability)

Question. 151

Given that -1 ≤ v ≤ 1, -2 ≤ u ≤ -0.5 and -2 ≤ z ≤ -0.5 and w = vz/u , then which of the following is necessarily true?

CAT/2003(Quantitative Ability)

Question. 152

If x, y, z are distinct positive real numbers then 

 

would be

CAT/2003(Quantitative Ability)

Question. 153

A test has 50 questions. A student scores 1 mark for a correct answer, –1/3 for a wrong answer, and 1/6 for not attempting a question. If the net score of a student is 32, the number of questions answered wrongly by that student can not be less than

CAT/2003(Quantitative Ability)

Question. 154

The number of roots common between the two equations x³ + 3x² + 4x + 5 = 0 and x³ + 2x² + 7x + 3 = 0 is

CAT/2003(Quantitative Ability)

Question. 155

A real number x satisfying 1 - 1/n < x ≤ 3 + 1/n  for every positive integer n, is best described by

CAT/2003(Quantitative Ability)

Question. 156

If x and y are integers then the equation 5x + 19y = 64 has

CAT/2003(Quantitative Ability)

Question. 157

If both a and b belong to the set {1, 2, 3, 4}, then the number of equations of the form ax² + b x + 1 = 0 having real roots is

CAT/2003(Quantitative Ability)

Question. 158

If three positive real numbers x, y, z satisfy y – x = z – y and x y z = 4, then what is the minimum possible value of y?

CAT/2003(Quantitative Ability)

Question. 159

CAT/2003(Quantitative Ability)

Question. 160

If 13x + 1 < 2z and z + 3 = 5y² , then

CAT/2003(Quantitative Ability)

Question. 161

If |b| ≥ 1 and x = – | a | b, then which one of the following is necessarily true?

CAT/2003(Quantitative Ability)

Question. 162

The sum of 3rd and 15th elements of an arithmetic progression is equal to the sum of 6th, 11th and 13th elements of the progression. Then, which element of the series should necessarily be equal to zero

CAT/2003(Quantitative Ability)

Question. 163

The 288th term of the series a, b, b, c, c, c, d, d, d, d, e, e, e, e, e, f, f, f, f, f, f.................is

CAT/2003(Quantitative Ability)

Question. 164

If log₃ 2, log₃(2^x - 5), log₃(2^x - 7/2) are in arithmetic progression, then the value of x is equal to

CAT/2003(Quantitative Ability)

Question. 165

There are 8436 steel balls, each with a radius of 1 centimeter, stacked in a pile, with 1 ball on top, 3 balls in the second layer, 6 in the third layer, 10 in the fourth, and so on. The number of horizontal layers in the pile is

CAT/2003(Quantitative Ability)

Question. 166

In a certain examination paper, there are n questions. For j = 1,2 ....n, there are 2n–j students who answered j or more questions wrongly. If the total number of wrong answers is 4095, then the value of n is

CAT/2003(Quantitative Ability)

Question. 167

CAT/2003(Quantitative Ability)

Question. 168

CAT/2002(Quantitative Ability)

Question. 169

If x, y and z are real numbers such that, x + y + z = 5 and xy + yz + zx = 3

What is the largest value that x can have?

CAT/2002(Quantitative Ability)

Question. 170

If x² + 5y² + z² = 2y(2x + z) then which of the following statements are necessarily true?

I. x = 2 y

II. x = 2 z

III. 2x = z

CAT/2002(Quantitative Ability)

Question. 171

The number of real roots of the equation A²/x + B²/(x - 1) = 1 where A and B are real numbers not equal to zero simultaneously is

CAT/2002(Quantitative Ability)

Question. 172

CAT/2002(Quantitative Ability)

Question. 173

A piece of string is 40 centimeters long. It is cut into three pieces. The longest piece is 3 times as long as the middle-sized piece and the shortest piece is 23 centimeters shorter than the longest piece. Find the length of the shortest piece.

CAT/2002(Quantitative Ability)

Question. 174

Three pieces of cakes of weight 4(1/2) lbs, 6(3/4) lbs and 7(1/5) lbs respectively are to be divided into parts of equal weights. Further, each part must be as heavy as possible. If one such part is served to each guest, then what is the maximum number of guests that could be entertained?

CAT/2002(Quantitative Ability)

Question. 175

The nth element of a series is represented as X_n = (–1)ⁿ X_{n – 1}

If X₀ = x and x > 0 then which of the following is always true

CAT/2002(Quantitative Ability)

Question. 176

CAT/2002(Quantitative Ability)

Question. 177

Amol was asked to calculate the arithmetic mean of ten positive integers each of which had two digits. By mistake, he interchanged the two digits, say a and b, in one of these ten integers. As a result, his answer for the arithmetic mean was 1.8 more than what it should have been. Then b – a equals

CAT/2002(Quantitative Ability)

Question. 178

A child was asked to add first few natural numbers (that is, 1 + 2 + 3 + .....) so long his patience permitted. As he stopped he gave the sum as 575. When the teacher declared the result wrong the child discovered he had missed one number in the sequence during addition. The number he missed was

CAT/2002(Quantitative Ability)

Question. 179

CAT/2001(Quantitative Ability)

Question. 180

If x > 5 and y < – 1, then which of the following statements is true?

CAT/2001(Quantitative Ability)

Question. 181

Two men X and Y started working for a certain company at similar jobs on January 1, 1950. X asked for an initial salary of Rs 300 with an annual increment of Rs 30. Y asked for an initial salary of Rs 200 with a rise of Rs 15 every six months. Assume that the arrangements remained unaltered till December 31, 1959. Salary is paid on the last day of the month. What is the total amount paid to them as salary during the period?

CAT/2001(Quantitative Ability)

Question. 182

x and y are real numbers satisfying the conditions 2 < x < 3 and – 8 < y < – 7. Which of the following expressions will have the least value?

CAT/2001(Quantitative Ability)

Question. 183

m is the smallest positive integer such that for any integer n ≤ m , the quantity n³ - 7n² + 11n - 5 is positive. What is the value of m?

CAT/2001(Quantitative Ability)

Question. 184

Let x, y be two positive numbers such that x + y = 1. Then, the minimum value of 

CAT/2001(Quantitative Ability)

Question. 185

Let b be a positive integer and a = b² – b. If b ≤ 4, then a² – 2a is divisible by

CAT/2001(Quantitative Ability)

Question. 186

Ujakar and Keshab solve a quadratic equation. Ujakar made a mistake in writing down the constant term. He ended up with the roots (4, 3). Keshab made a mistake in writing down the coefficient of x. He got the roots as (3, 2). What will be the exact roots of the original quadratic equation?

Comprehension

Directions for questions: Read the information given below and answer the questions that follow :

The batting average (BA) of a test batsman is computed from runs scored and innings played - completed innings and incomplete innings (not out) in the following manner :

CAT/2001(Quantitative Ability)

Question. 187

Based on the information provided which of the following is true?

Comprehension

Directions for questions: Read the information given below and answer the questions that follow :

The batting average (BA) of a test batsman is computed from runs scored and innings played - completed innings and incomplete innings (not out) in the following manner :

CAT/2001(Quantitative Ability)

Question. 188

An experienced cricketer with no incomplete innings has a BA of 50. The next time he bats, the innings is incomplete and he scores 45 runs. It can be inferred that

CAT/2001(Quantitative Ability)

Question. 189

All the page numbers from a book are added, beginning at page 1. However, one page number was mistakenly added twice. The sum obtained was 1000. Which page number was added twice?

CAT/2001(Quantitative Ability)

Question. 190

If a, b, c and d are four positive real numbers such that abcd = 1 , what is the minimum value of (1 + a) (1 + b) (1 + c) (1 + d)?

CAT/2001(Quantitative Ability)

Question. 191

For a Fibonacci sequence, from the third term onwards, each term in the sequence is the sum of the previous two terms in that sequence. If the difference in squares of seventh and sixth terms of this sequence is 517, what is the tenth term of this sequence?

CAT/2000(Quantitative Ability)

Question. 192

x > 2, y > 1 then which of the following holds good ? 

CAT/2000(Quantitative Ability)

Question. 193

A, B and C are 3 cities that form a triangle and where every city is connected to every other one by at least one direct roots. There are 33 routes direct & indirect from A to C and there are 23 direct routes from B to A. How many direct routes are there from A to C ?

CAT/2000(Quantitative Ability)

Question. 194

If the equation x³ - ax² + bx - a = 0 has three real roots then which of the following is true?

CAT/2000(Quantitative Ability)

Question. 195

CAT/2000(Quantitative Ability)

Question. 196

CAT/2000(Quantitative Ability)

Question. 197

CAT/1999(Quantitative Ability)

Question. 198

| r - 6 |=11 and | 2q - 12 |= 8, then what is the minimum value of q / r?

CAT/1999(Quantitative Ability)

Question. 199

The expenses of a boarding school depends upon the fixed cost and variable cost. Variable cost varies directly as the number of students. If the expenses per student were Rs 600 for 50 students and Rs 700 for 25 students then what are the expenses for 100 students?

Comprehension

Directions for Questions: These questions are based on the situation given below :

There are fifty integers a₁ , a₂ , ....... a₅₀, not all of them necessarily different. Let the greatest integer of these fifty integers be referred to as G, and the smallest integer be referred to as L. The integers a₁ through a₂₄ form sequence S1, and the rest form sequence S2. Each member of S1 is less than or equal to each member of S2.

CAT/1999(Quantitative Ability)

Question. 200

All values in S1 are changed in sign, while those in S2 remain unchanged. Which of the following statements is true?

Comprehension

Directions for Questions: These questions are based on the situation given below :

There are fifty integers a₁ , a₂ , ....... a₅₀, not all of them necessarily different. Let the greatest integer of these fifty integers be referred to as G, and the smallest integer be referred to as L. The integers a₁ through a₂₄ form sequence S1, and the rest form sequence S2. Each member of S1 is less than or equal to each member of S2.

CAT/1999(Quantitative Ability)

Question. 201

Elements of S1 are in ascending order, and those of S2 are in descending order. a₂₄ and a₂₅ are interchanged then which of the following statements is true

CAT/1999(Quantitative Ability)

Question. 202

There are fifty integers a₁ , a₂ , ....... a₅₀, not all of them necessarily different. Let the greatest integer of these fifty integers be referred to as G, and the smallest integer be referred to as L. The integers a₁ through a₂₄ form sequence S1, and the rest form sequence S2. Each member of S1 is less than or equal to each member of S2.

Every element of S1 is made greater than or equal to every element of S2 by adding to each element of S1an integer x.Then x cannot be less than

Comprehension

There are m blue vessels with known volumes V1, V2,....., Vm arranged in ascending order of volumes, where V1 is greater than 0.5 litres and Vm is less than 1 litre. Each of these is full of water. The water is emptied into a minimum number of white empty vessels each having volume 1 litre. If the volumes of the vessels increases with the value of lower bound 10^–1 .

CAT/1999(Quantitative Ability)

Question. 203

What is the maximum possible value of m?

Comprehension

There are m blue vessels with known volumes V1, V2,....., Vm arranged in ascending order of volumes, where V1 is greater than 0.5 litres and Vm is less than 1 litre. Each of these is full of water. The water is emptied into a minimum number of white empty vessels each having volume 1 litre. If the volumes of the vessels increases with the value of lower bound 10^–1 .

CAT/1999(Quantitative Ability)

Question. 204

If m is maximum then what is the minimum number of white vessels required to empty it?

Comprehension

There are m blue vessels with known volumes V1, V2,....., Vm arranged in ascending order of volumes, where V1 is greater than 0.5 litres and Vm is less than 1 litre. Each of these is full of water. The water is emptied into a minimum number of white empty vessels each having volume 1 litre. If the volumes of the vessels increases with the value of lower bound 10^–1 .

CAT/1999(Quantitative Ability)

Question. 205

If m is maximum then what is range of the volume remaining empty in the vessel with the maximum empty space?

CAT/1998(Quantitative Ability)

Question. 206

One year payment to a servant is Rs 90 plus one turban. The servant leaves after 9 months and receives Rs 65 and a turban. Then find the price of the turban

CAT/1998(Quantitative Ability)

Question. 207

You can collect Rubies and Emeralds as many as you can. Each Ruby is worth Rs 4crores and each Emerald is worth of Rs 5crore. Each Ruby weights 0.3 kg. and each Emerald weighs 0.4 kg. Your bag can carry at the most 12 kg. What you should collect to get the maximum wealth?

CAT/1997(Quantitative Ability)

Question. 208

If the roots, x₁ and x₂ , of the quadratic equation x² – 2x + c = 0 also satisfy the equation 7x_² – 4x₁ = 47, then which of the following is true?

CAT/1997(Quantitative Ability)

Question. 209

If log₂ [log₇ (x² – x + 37)] = 1, then what could be the value of x?

CAT/1996(Quantitative Ability)

Question. 210

Once I had been to the post-office to buy stamps of five rupees, two rupees and one rupee. I paid the clerk Rs 20, and since he did not have change, he gave me three more stamps of one rupee. If the number of stamps of each type that I had ordered initially was more than one, what was the total number of stamps that I bought?

CAT/1996(Quantitative Ability)

Question. 211

Given the quadratic equation x² – (A – 3)x – (A – 7), for what value of A will the sum of the squares of the roots be zero?

CAT/1996(Quantitative Ability)

Question. 212

Which of the following values of x do not satisfy the inequality (x² - 3x + 2 > 0) at all?

CAT/1996(Quantitative Ability)

Question. 213

Out of two-thirds of the total number of basket-ball matches, a team has won 17 matches and lost 3 of them. what is the maximum number of matches that the team can lose and still win three-fourths of the total number of matches, if it is true that no match can end in a tie ?

CAT/1995(Quantitative Ability)

Question. 214

What is the value of m which satisfies 3m² – 21m + 30 < 0 ?

CAT/1995(Quantitative Ability)

Question. 215

CAT/1995(Quantitative Ability)

Question. 216

One root of x² + kx – 8 = 0 is square of the other. Then the value of k is

CAT/1994(Quantitative Ability)

Question. 217

CAT/1994(Quantitative Ability)

Question. 218

CAT/1994(Quantitative Ability)

Question. 219

Nineteen years from now Jackson will be 3 times as old as Joseph is now. Joseph is three years younger than Jackson.

I. Johnson’s age now

II. Joseph’s age now

CAT/1994(Quantitative Ability)

Question. 220

log 216√6 to the base 6 is

CAT/1994(Quantitative Ability)

Question. 221

If log₇ log₅ (√x + 5 + √x ) = 0 , find the value of x.

CAT/1994(Quantitative Ability)

Question. 222

If the harmonic mean between two positive numbers is to their geometric mean as 12 : 13; then the numbers could be in the ratio

CAT/1994(Quantitative Ability)

Question. 223

Fourth term of an arithmatic progression is 8. What is the sum of the first 7 terms of the arithmatic progression?

CAT/1994(Quantitative Ability)

Question. 224

Along a road lie an odd number of stones placed at intervals of 10 m. These stones have to be assembled around the middle stone. A person can carry only one stone at a time. A man carried out the job starting with the stone in the middle, carrying stones in succession, thereby covering a distance of 4.8 km. Then the number of stones is